Programmazione lineare
Problema risolto con l’ausilio di EXCEL e Derive
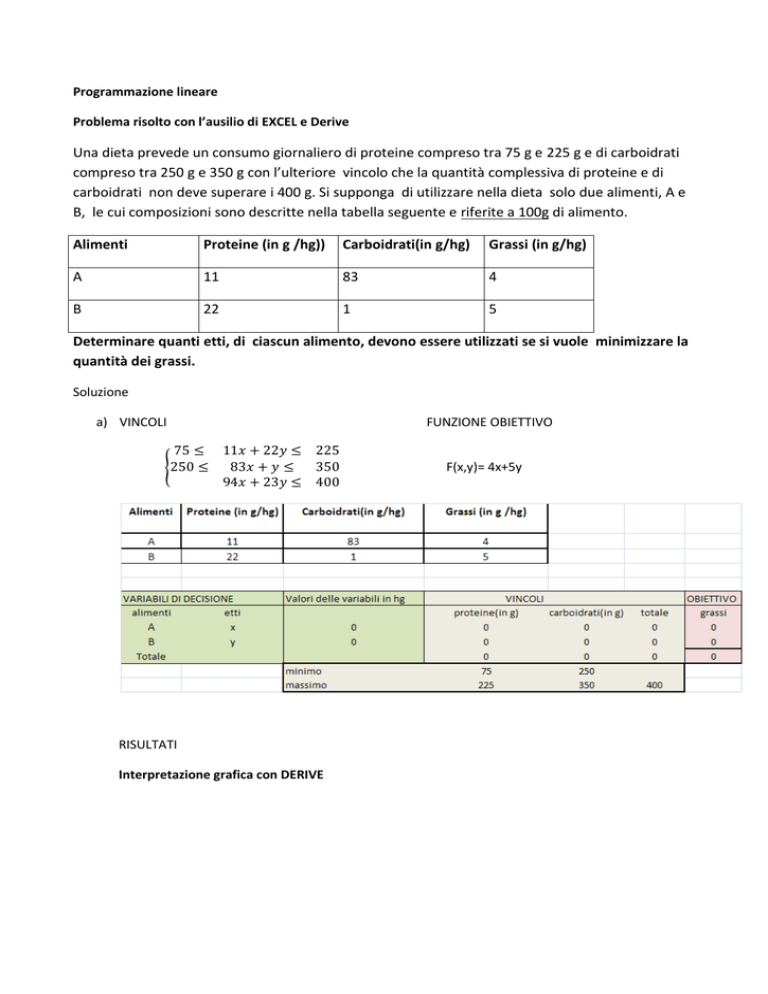
Una dieta prevede un consumo giornaliero di proteine compreso tra 75 g e 225 g e di carboidrati
compreso tra 250 g e 350 g con l’ulteriore vincolo che la quantità complessiva di proteine e di
carboidrati non deve superare i 400 g. Si supponga di utilizzare nella dieta solo due alimenti, A e
B, le cui composizioni sono descritte nella tabella seguente e riferite a 100g di alimento.
Alimenti
Proteine (in g /hg))
Carboidrati(in g/hg)
Grassi (in g/hg)
A
11
83
4
B
22
1
5
Determinare quanti etti, di ciascun alimento, devono essere utilizzati se si vuole minimizzare la
quantità dei grassi.
Soluzione
a) VINCOLI
FUNZIONE OBIETTIVO
F(x,y)= 4x+5y
RISULTATI
Interpretazione grafica con DERIVE
Risultati ottenuti con il Risolutore di EXCEL
Rapporto -Valori
Rapporto di sensibilità
ANALISI DEI RISULTATI
Dal rapporto_valori di Excel e dall’immagine visualizzata con Derive si evince che i vincoli attivi sono solo
2, precisamente
vincolo di minimo sulla quantità di proteine
vincolo di minimo sulla quantità di carboidrati
E’ facile verificare che le soluzioni delle due disequazioni corrispondono proprio alla coppia di semipiani
sulla cui frontiera si trova il punto ottimale
Questo significa che solo alterando uno di questi due vincoli si otterrà una variazione del risultato, come si
può verificare velocemente cambiando , uno alla volta, i valori minimi e i valori massimi previsti.