MODELLI PER VARIABILI ALEATORIE CONTINUE
VARIABILE ALEATORIA UNIFORME CONTINUA
Una v.a. continua rappresenta fenomeni uniformemente ripartiti in un intervallo, ossia:
- assume valori solo nell’intervallo [a,b]
- a sottoinsiemi di [a,b] di uguale ampiezza corrispondono uguali probabilità.
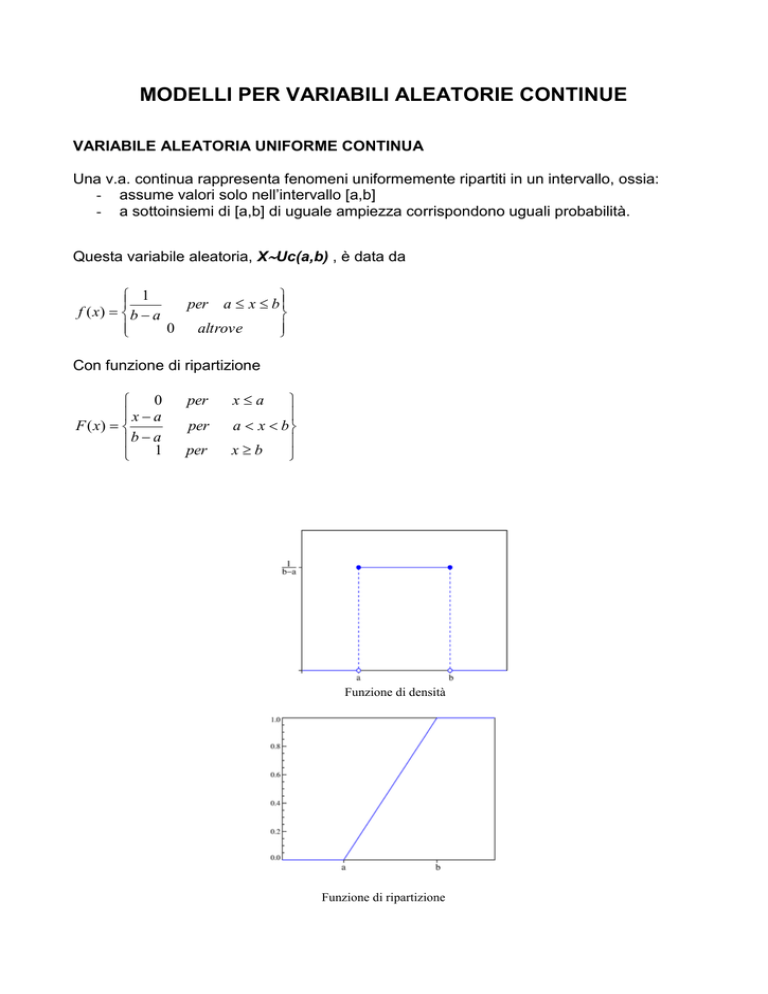
Questa variabile aleatoria, XUc(a,b) , è data da
1
per a x b
f ( x) b a
0
altrove
Con funzione di ripartizione
0
x a
F ( x)
b a
1
per
per
per
xa
a x b
xb
Funzione di densità
Funzione di ripartizione
Rispettivamente media, varianza, asimmetria e curtosi sono pari a:
ab
2
(b a ) 2
Var ( X )
12
Asym( X ) 0
Kurt ( X ) 1.8
E( X )
VARIABILE ALEATORIA ESPONENZIALE NEGATIVA
Si tratta di una v.a. continua che descrive la "durata di vita" di un fenomeno privo di
memoria.
Un esempio è la durata di vita di una particella radioattiva prima di decadere.
La distribuzione esponenziale XEn() , con parametro
, ha funzione di densità di
probabilità definita sui numeri reali positivi
pari alla funzione esponenziale
0
per x>0
altrove
La funzione è decrescente da x=0, dove f(0)= , valore massimo. Dunque la moda è
uguale a zero.
La funzione di ripartizione sarà
x
F ( x) exp( )d [ exp( )]0x 1 exp( )
0
Funzione di densità
x 0
Funzione di ripartizione
in particolare si ha la formula P(X > x) = e − λx perché P(X > x) = 1 - P(X = x). Questo
implica la mancanza di memoria, infatti
P(X > a + b) = P(X > a)P(X > b)
Fra le distribuzioni di probabilità discrete, invece, ogni distribuzione priva di memoria è una
distribuzione geometrica.
Valor medio, varianza, asimmetria e curtosi valgono
E( X )
1
Var ( X )
1
2
Asym( X ) 2
Kurt ( X ) 9.
La v.a. esponenziale negativa è correlata alla v.a. di Poisson, perché se gli eventi della
v.a., che rappresenta il numero di arrivi nel tempo, sono distribuiti come la v.a. di Poisson,
allora i tempi sono distribuiti come la v.a. esponenziale negativa con il medesimo
parametro .
Vedremo anche che la v.a. esponenziale con 1 / 2 corrisponde alla v.a. chi quadrato
con due gradi di libertà, χ2(2).
La v.a. Gamma XGa(, ) generalizza la distribuzione esponenziale: Ga(1,1 / λ)
coincide con En(). In particolare, la somma Y = X1 + ... + Xn di n variabili aleatorie
indipendenti di medesima legge esponenziale con parametro λ segue la distribuzione
Gamma Ga(n,1 / λ).
L’espressione della variabile aleatoria Gamma è
f ( x, , )
1
x exp( x)
( )
per
x 0, 0
( ) x 1 exp( x)dx
0
E’ interessante sottolineare che per valori interi vale
( ) ( 1)!
(1 / 2)
Un esempio: la radioattività
Il tempo di decadimento di un isotopo radioattivo viene solitamente modellizzato in
funzione della sua vita media tramite la distribuzione esponenziale con. λ = 1 / τ è detto
costante di decadimento; la speranza di vita è proprio E[X] = 1 / λ = τ.
Con questo modello si possono ad esempio calcolare le probabilità che l'isotopo decada in
meno della metà del tempo medio,
,
o in più del doppio di questo tempo
.
Ciononostante un osservatore che non abbia ancora visto decadere l'isotopo si ritrova
nuovamente nelle condizioni iniziali, a causa dell'assenza di memoria; dovrà quindi
aspettare sempre mediamente un tempo τ prima del decadimento.
In un campione con un numero di isotopi molto grande (come avviene solitamente), le
probabilità di ogni singolo isotopo (indipendente dagli altri) si possono tradurre in
percentuali del campione. Ad esempio, il tempo medio dopo il quale metà dei campioni
decadono (emivita o tempo di dimezzamento) è dato dalla mediana, che vale (log2) / λ.
LA VARIABILE ALEATORIA DI LAPLACE-GAUSS O NORMALE
La distribuzione binomiale permette di calcolare, per numeri n piccoli, le probabilità di
avere un certo numero k di successi nelle n prove.
Se abbiamo molte prove, n diventa molto grande eTrovare le probabilità dei successi k
diventa difficile. D’altra parte per alti n il problema non è di trovare la probabilità connessa
ad uno specifico numero k di successi, ma di trovare ad esempio la probabilità di trovare
più o meno di k successi.
Si ricorre allora alla distribuzioni NORMALE ( GAUSSIANA) XN(,2) che vale per n
molto grande.
In questo caso lo scaloide della distribuzione di probabilità binomiale, ossia l’insieme dei
rettangoli che rappresentano le probabilità dei singoli k, tende a diventare un’area
sottostante ad una linea continua.
La forma della curva cui tende la distribuzione al tendere di n all’infinito è differente
secondo il valore che p (e quindi q) assume.
Si danno due casi:
•
Nel primo caso p e q non sono molto differenti fra loro e quindi nessuno dei due
valori si scosta molto dal valore di probabilità ½. In questo caso al tendere di n
all’infinito la distribuzione tende alla curva teorica che è la gaussiana. Si intende di
solito che una distribuzione di probabilità è normale quando il prodotto np è
maggiore di 5 (nel caso p>q).
•
Nel secondo caso p è molto maggiore o molto minore di q, in modo che ambedue si
discostano molto da probabilità ½. Se al tendere di n all’infinito il prodotto p n
rimane costante, la distribuzione tende alla cosiddetta curva di Poisson. Si parla di
poissoniana quando il prodotto np << n.
Una distribuzione binomiale è simmetrica solo se n=p=1/2. Anche una distribuzione
normale è in generale asimmetrica, ma diventa simmetrica al crescere di n. Per n è
perfettamente simmetrica: f(x)=f(-x) , punto massimo in corrispondenza di e
coincidente con moda e mediana.
Inoltre
Asym( X ) 0
Kurt ( X ) 3
Data una grandezza x distribuita normalmente con media e deviazione standard ,
l’equazione della curva normale è
x -
1/2(
1
f(x)
e
2
)2
per x .
Ricordiamo che f(x) non dà la probabilità associata ad x, bensì la densità di probabilità.
Per ottenere la probabilità associata ad un evento relativo ad una distribuzione normale
occorre integrare su un intervallo appropriato.
Ad esempio la probabilità che x sia minore di x0 sarà
P( x x0 )
x0
f(x)
x0
2
2
1
e 1/2(xμ) /σ dx
σ 2π
Invece la probabilità che x sia compreso fra due valori x1 e x2 sarà
P( x1 x x2 )
x2
x1
f(x)
x2
x1
2
2
1
e 1/2(xμ) /σ dx
σ 2π
Sappiamo che l’area delimitata dalla curva e dall’asse x vale 1. Quindi l’area sotto la curva
compresa fra le due ordinate x=a e x=b , dove a<b, rappresenta la probabilità che x sia
compreso fra a e b.
Quando la variabile x viene espressa in unità standard,
z= (x -)/
l’equazione precedente viene sostituita dalla sua FORMA STANDARDIZZATA ZN(0,1)
f(z)
2
1
e 1/2 z
2
e in tal caso diciamo che z è distribuita normalmente con media zero e varianza uno. Il
grafico sarà simmetrico intorno allo zero.
Nel caso di approssimazione della distribuzione binomiale a quella normale si avrà
=np
=npq
x=k numero di successi su n prove
Rappresentando graficamente questa funzione otteniamo la caratteristica curva a
campana simmetrica intorno alla media:
In corrispondenza di + e – la curva presenta i suoi punti di flesso.
Tracciando diversi diagrammi per diversi valori di ci accorgiamo che la curva è tanto
più appiattita quanto maggiore è la deviazione standard.
Una proprietà fondamentale della gaussiana è la seguente:
-esiste una probabilità definita e uguale per tutte le curve normali che un certo scarto
sia inferiore a una (2, 3) deviazione standard.
Tale probabilità è equivalente all’area tratteggiata in figura:
•
•
•
Probabilità che un valore cada casualmente entro alcune deviazioni standard:
-
Entro 1.0 d.s. dalla media = 68.26%
Entro 1.96 d.s. dalla media = 95.00%
Entro 2.0 d.s. dalla media = 95.44%
Entro 2.575 d.s. dalla media = 99.00%
Entro 3.0 d.s. dalla media = 99.73%
Entro 3.29 d.s. dalla media = 99.90%
Ossia il 95% delle osservazioni cade entro 1.96 d.s., ed entro 3 d.s. sono comprese
pressochè tutte le osservazioni.
L’utlità della variabile standardizzata sta nell’indipendenza dall’unità di misura e nel fatto
che essa è adattabile alle infinite gaussiane. Infatti ogni distribuzione normale può avere
un numero infinito di valori per media e scarto quadratico medio, quindi sarebbe
impossibile tabulare l’area associata ad ogni singola curva.
Invece i valori dell’area sotto la curva standardizzata sono tabulati e grazie alla sua
simmetria è sufficiente tabulare solo metà della funzione.
UTILIZZO DELLE TAVOLE
La tavola seguente fornisce i valori della probabilità
P(Zz )= (Z=z)
dove (Z=z) è la funzione di ripartizione.
Esempio:
Determinare la probabilità
P(-0.25<Z<0.75) .
Si tiene conto del fatto che
P( z1 Z z 2 ) (Z z 2 ) (Z z1 )
Dunque
P(-0.25<Z<0.75)=(0.75)-(0.25) .
Si cerca sulla tavola il valore (0.75) procedendo lungo la colonna verticale fino al valore
0.5, poi lungo l’orizzontale fino a 5. Si legge così il valore 0.77337.
Per il valore (-0.25) si considera che (-0.25)= 1 - (025).
Si ricerca analogamente sulla tavola il valore per (0.25), che è 0.59871. Si ottiene allora
P(-0.25<Z<0.75)=0.77337 – 0.40129=0.37208.
VARIABILE ALEATORIE DEDOTTE DALLA NORMALE
LA VARIABILE ALEATORIA CHI QUADRATO
La v.a. Chi quadrato (X 2 ) E’ una v.a. continua ottenuta dalla somma di un numero g di
v.a. normali standardizzate e indipendenti al quadrato:
g
X Z i2
i 1
Il parametro g indica i gradi di libertà della distribuzione, ossia il numero di unità di
informazioni indipendenti relative al campione. Si calcolano sottraendo alla numerosità
campionaria il numero dei vincoli, ossia i parametri noti della popolazione.
La funzione densità si esprime con
f ( x; g )
g
1
x
exp( ) x 2
g
2
2 g / 2 ( )
2
1
per
x0
Si vede quindi che, come si era già detto, si tratta di un caso particolare della v.a. Gamma
per =g/2 e =1/2 .
La funzione non è simmetrica ma è unimodale (ossia media e moda coincidono).
La tavola in fondo fornisce I quantili della distribuzione t in corrispondenza ai gradi di
libertà. In caso di numero di gradi di libertà mancante, si ricorre ad interpolazione.
Funzione densità
Funzione di ripartizione
Si ha:
E( X ) g
Var ( X ) 2 g
8
Asym( X )
g
12
Kurt ( X ) 3
g
Al crescere dei gradi di libertà la chi quadrato tende alla normale.
Una tavola apposita (v. in fondo al documento) fornisce i suoi quantili, ossia i valori di
2 che, per differenti gradi di libertà, valorizzano le proporzioni nella coda di destra della
distribuzione.
LA VARIABILE ALEATORIA t di STUDENT
Questa v.a. (dallo pseudonimo del matematico inglese W. Gosset) è data dal rapporto fra
una v.a. normale standardizzata e la radice quadrata di una v.a. chi quadarato
indipendente dalla prima e rapportata ai propri gradi di libertà,
Z
X
Y
g
Dove Y= 2 .
La sua funzione di densità è
g 1
)
( g 1)
x2
2
f ( x; g )
(1 ) 2
g
g
g ( )
2
(
per x
Con media, varianza, asimmetria e curtosi pari a
E( X ) 0
per
g 1
g
Var ( X )
per g 2
g 2
Asym( X ) 0
6
Kurt ( X ) 3
per g 4
g 4
Quindi si vede che per g le espressioni diventano
E( X ) 0
Var ( X ) 1
Asym( X ) 0
Kurt ( X ) 3
Ossia la distribuzione t di Student tende a duna v.a. standardizzata Z.
La curva è simmetrica unimodale e si sovrappone alla gaussiana per g>30.
LA VARIABILE ALEATORIA F DI FISHER
La v.a. di Fisher F Fg1, g 2 è definita come il rapporto di due v.a. chi quadrato indipendenti
fra loro e divise per i rispettivi gradi di libertà:
X 1 g1
2
X 2 g2
2
Fg1, g 2
X 1 / g1
X 2 / g2
dove g1 e g2 sono i gradi di libertà di numeratore e di denominatore.
La funzione di densità ha la forma
[( g1 g 2) / 2
f ( x, g1, g 2)
( g1 / g 2) 2
( g1 / 2)( g 2 / 2)
x ( g1 / 2 ) 1
g1
(1
g1
x)( g1 g 2) / 2
g2
e valor medio e varianza sono
E( X )
g2
g2 2
Var ( X )
per
g2 2
2( g 2) 2 ( g1 g 2 2)
g1( g1 2) 2 ( g 2 4)
per
g2 4
Asimmetria e curtosi hanno espressioni complesse.
La F di Fisher si usa per confrontare la variabilità di due insiemi di dati, ed è fondamentale
nell’analisi della varianza.
In fondo è riportata la tavola dei quantili della v.a. di Fisher .
LA VARIABILE ALEATORIA LOGNORMALE
Si tratta della trasformazione logaritmica della distribuzione normale.
Se X è una v.a. con distribuzione lognormale, la v.a. Y=log X è una variabile con
distribuzione normale.
La distribuzione dà luogo ad una curva con coda allungata a destra (asimmetria sinistra).
Si adotta nel caso di distribuzioni di probabilità in cui si registra addensamento su valori
medio bassi e rarefazione di probabilità all’aumentare dei valori: ad esempio nel caso del
reddito o della dimensione dei nuclei familiari.
La funzione di densità ha la forma
f ( x)
(ln x ) 2
exp
2
x 2
2
1
Dove e sono valore atteso e scarto quadratico medio del logaritmo della v.a. X, che
come si è detto ha distribuzione gaussiana.
X ha ovviamente la limitazione di assumere solo valori positivi.
La funzione di distribuzione cumulativa si ottiene integrando la funzione
F ( x) (
ln x
2
)
e media e varianza sono
E ( X ) exp(
2
)
2
Var ( X ) exp( 2 2 )(exp( 2 ) 1)
Tutte queste distribuzioni derivate dalla normale assumono importanza nella statistica
inferenziale perché vengono utilizzate nei test di significatività che verranno esposti
successivamente.












