IL TEOREMA DI PITAGORA
Questo teorema era già noto ai babilonesi, ma fu il matematico greco Pitagora, intorno al 500 a.C., a darne una
descrizione precisa.
ENUNCIATO: la somma dei quadrati costruiti sui cateti è equivalente al quadrato costruito sull’ipotenusa.
AB 2 + AC 2 = BC 2
Q1 + Q2 = Q3
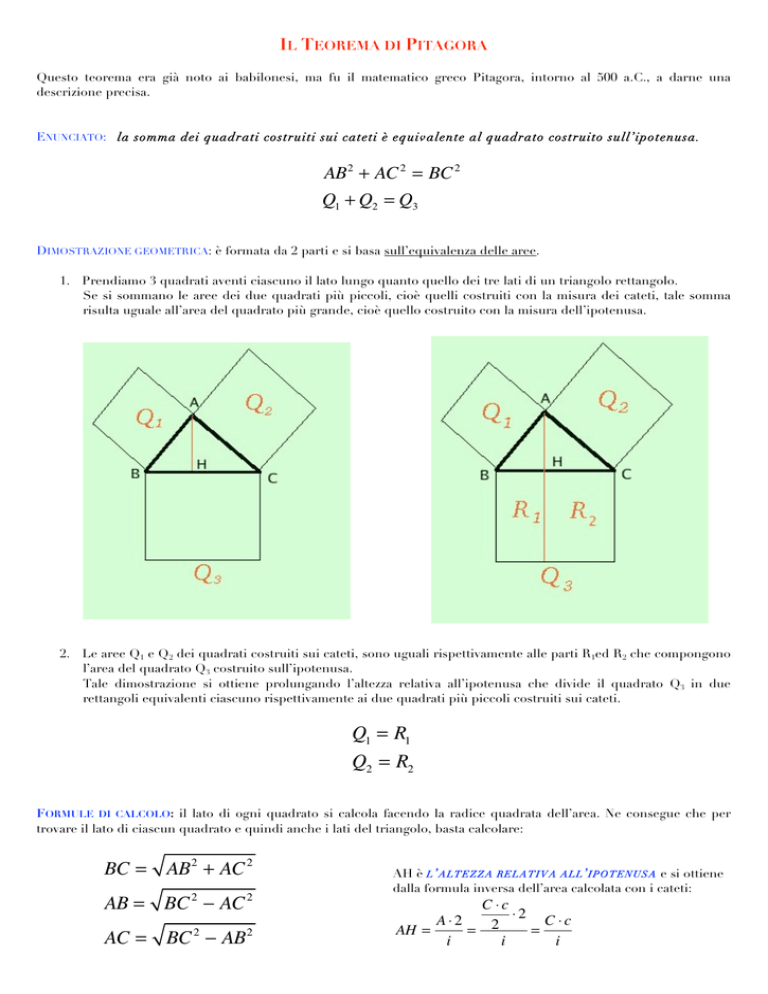
DIMOSTRAZIONE GEOMETRICA: è formata da 2 parti e si basa sull’equivalenza delle aree.
1. Prendiamo 3 quadrati aventi ciascuno il lato lungo quanto quello dei tre lati di un triangolo rettangolo.
Se si sommano le aree dei due quadrati più piccoli, cioè quelli costruiti con la misura dei cateti, tale somma
risulta uguale all’area del quadrato più grande, cioè quello costruito con la misura dell’ipotenusa.
2. Le aree Q1 e Q2 dei quadrati costruiti sui cateti, sono uguali rispettivamente alle parti R1ed R2 che compongono
l’area del quadrato Q3 costruito sull’ipotenusa.
Tale dimostrazione si ottiene prolungando l’altezza relativa all’ipotenusa che divide il quadrato Q3 in due
rettangoli equivalenti ciascuno rispettivamente ai due quadrati più piccoli costruiti sui cateti.
Q1 = R1
Q2 = R2
FORMULE DI CALCOLO: il lato di ogni quadrato si calcola facendo la radice quadrata dell’area. Ne consegue che per
trovare il lato di ciascun quadrato e quindi anche i lati del triangolo, basta calcolare:
BC = AB 2 + AC 2
AB = BC 2 − AC 2
AC = BC 2 − AB 2
AH è L ’ ALTEZZA RELATIVA ALL ’ IPOTENUSA e si ottiene
dalla formula inversa dell’area calcolata con i cateti:
A⋅2
AH =
=
i
C ⋅c
⋅2 C ⋅c
2
=
i
i
ES: Un triangolo rettangolo ha l’ipotenusa che misura 30 cm e il cateto minore che misura 18 cm. Calcola l’altezza
relativa all’ipotenusa, il perimetro e area del triangolo.
DATI
AB = 30 cm
BC = 18 cm
INCOGNITA
? = A ABC
? = P ABC
? = AH
RISOLVO
AC = AB 2 − BC 2 = 30 2 − 18 2 = 900 − 324 = 576 = 24cm
AH = C ⋅ c = 24 ⋅18 = 14, 4cm
i
30
PABC= 30 + 18 + 24 = 72 cm
AABC= C ⋅ c = 18 ⋅ 24 = 216cm 2
2
2
oppure
AABC = i ⋅ AH = 30 ⋅14, 4 = 216cm 2
2
2
TERNE PITAGORICHE
Una terna pitagorica è una serie di tre numeri differenti (tutti interi o in parte decimali limitati) che rappresentano i
tre valori dei lati di un triangolo rettangolo e che soddisfano il teorema di Pitagora.
Se uno dei numeri è un decimale illimitato, la terna non è pitagorica: (Es: se i cateti sono 5 e 6, l’ipotenusa è 7,8103...)
Se la terna è pitagorica abbiamo:
Il numero più piccolo rappresenta il cateto minore ( a );
Il numero medio rappresenta il cateto maggiore ( b );
Il numero più grande rappresenta l’ipotenusa ( c ).
Le terne possono essere:
•
P RIMITIVE - formate da numeri primi fra loro.
(Es: 3; 4 ; 5)(5; 12; 13)(14; 48; 50)(6; 17,5; 18,5)
•
M ULTIPLE - si ottengono moltiplicando una terna primitiva per un multiplo comune.
(Es: 3; 4 ; 5) x 2 = 6; 8; 10
COSTRUZIONE DI UNA TERNA PRIMITIVA: è necessario partire dal cateto minore. E’ importante capire se il cateto minore
è un numero pari o dispari, per ottenere terne primitive da differenti formule:
TRIANGOLI RETTANGOLI CON ANGOLI ACUTI PARTICOLARI
I problemi con tali triangoli presentano una quantità di dati inferiore rispetto a un problema con altri triangoli
rettangoli, poiché i lati sono uno sottomultiplo dell’altro:
•
UNO DA 30° E UNO DA 60°
(metà di un triangolo equilatero ABC)
Il lato opposto all’angolo da 30° (AH o cateto minore) è la metà dell’ipotenusa (AC)
Esistono delle formule per calcolare i lati che derivano dal teorema di Pitagora. Se chiamo l’ipotenusa con
ottengo:
a
ip = a
cat min =
a
2
cat magg = a
•
3
2
2 ANGOLI DA 45° (TRIANGOLO RETTANGOLO ISOSCELE)
(metà di un quadrato)
I due cateti hanno la stessa misura(AC e CB) e l’ipotenusa (AC) si trova come la diagonale di un
quadrato costruito su un cateto
Esistono delle formule per calcolare i cateti o l’ipotenusa che derivano dal teorema di Pitagora. Se chiamo
l’ipotenusa con a ottengo:
ip = cat 2
ip
cat =
2
Es: Un triangolo equilatero ha il lato di 12 cm. Trova l’area di un triangolo rettangolo isoscele avente l’ipotenusa
congruente all’altezza del triangolo equilatero.
DATI
AB = 12 cm
AH = A’C’
INCOGNITA
? = A’ABC
RISOLVO
BH = 1/2 AB = 12 : 2 = 6 cm
AH = AB 2 − BH 2 = 12 2 − 6 2 = 144 − 36 = 108 = 10, 39 = 10, 4cm
AC = AH = 10,4 cm
A’B’ = ip = 10, 4 = 7, 4cm
2 1, 414
AABC= l 2 = 7, 4 2 = 54, 76cm 2
APPLICAZIONE DEL TEOREMA DI PITAGORA ALLE ALTRE FIGURE
Alcune figure composte possono avere costruiti al loro interno triangoli rettangoli più piccoli, sui quali è possibile
applicare il teorema di Pitagora e calcolare così parti mancanti della figura composta.
ES: Un quadrato ha il perimetro di 48 cm. Esso è equivalente ai 12/35 di un trapezio isoscele avente l a base
maggiore tripla del perimetro del quadrato e la base minore metà del perimetro del quadrato.
Un parallelogramma con un angolo alla base che misura 30° ha il lato obliquo che misura 2/3 del lato del
quadrato e la base congruente al lato del quadrato.
Calcola:
• la misura della diagonale del quadrato;
• il perimetro del trapezio,dopo aver approssimato il lato obliquo allo 0,1;
• l’area del parallelogramma.












