Esercitazione di Analisi dei Sistemi 2

Analisi dei sistemi e Fisiologia – mod. Elementi di Analisi dei Sistemi
Esercitazione n°3
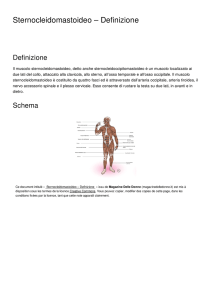
Il riflesso miotatico, quale quello rotuleo, può essere rappresentato come un sistema dinamico in retroazione
secondo lo schema seguente dove:
L0:
lunghezza del muscolo a riposo,
L:
lunghezza del muscolo,
∆Lm:
accorciamento del muscolo,
di:
sollecitazione impulsiva esterna,
Fm:
forza esercitata dalle fibre muscolari,
Fd:
forza esterna esercitata sul muscolo,
Ftot:
forza complessiva esercitata sul muscolo,
fe:
frequenza dello stimolo del neurone efferente,
fa:
frequenza dello stimolo del neurone afferente,
Gm(s):
funzione di trasferimento della dinamica del muscolo,
Gf(s):
funzione di trasferimento dei fusi del muscolo,
Kc:
coefficiente di guadagno del midollo spinale,
Km:
coefficiente di guadagno del muscolo,
L0
Fd
Km
fe
Fm
Kc
+
_
Ftot
fa
∆ Lm
Gm(s)
_
+
L
+
di
Gf(s)
+
La dinamica di allungamento/accorciamento del muscolo deve tenere conto della sua massa, dello
scorrimento delle fibre muscolari e dell'azione dei muscoli antagonisti. In prima approssimazione si può
rappresentare come un sistema meccanico caratterizzato da massa (m), attrito (b) e richiamo elastico (k),
rispettivamente:
G m  s=
K1
2
ms bsk
I fusi muscolari reagiscono ad allungamenti rapidi proporzionalmente all'allungamento ed alla sua velocità di
variazione; pertanto in prima approssimazione la loro funzione di trasferimento può caratterizzarsi da una
coppia zero-polo:
G f s =
K f 11 s 
1 2 s
Ipotizzando che i parametri del modello assumano i seguenti valori:
Kc· Km = 0.2;
Kf = 1
τ1 = 10;
τ2 = 0.1;
K1 = 0.5;
m= 1
b = 0.8;
k = 4;
Tracciare i diagrammi di Bode delle funzioni di trasferimento del muscolo e del fuso muscolare. Valutare
quindi la stabilità del sistema a ciclo chiuso attraverso il calcolo dei margini di stabilità della funzione di
trasferimento a ciclo aperto.
Calcolare infine la trasferimento tra l'uscita impulsiva di e la lunghezza del muscolo L.
Bozza soluzione esercitazione n° 3 di Elementi di analisi dei sistemi
Bozza soluzione esercitazione n° 3 di Elementi di analisi dei sistemi
Diagramma di Bode di Gm(s)
S ys te m : G m
F req u e nc y (rad /s e c): 1 .92
M ag n itud e (d B ): -9.9 4
0
B o d e D ia g r a m
M a g n itu d e ( d B )
-2 0
S ys te m : G m
F req u e nc y (rad /s e c ): 0 .11 4
M a g n itu d e (d B ): -1 8
-4 0
S ys te m : G m
F req u e nc y (rad /s e c): 1 0
M a g n it u d e (d B ): -4 5 . 7
-6 0
S ys te m : G m
F req u e nc y (rad /s e c ): 9 9.6
M a g n itud e (d B ): -8 6
-8 0
-1 00
0
S ys te m : G m
F req u e nc y (rad /s e c): 1
P ha s e (de g ): -1 5
P h a s e (d e g )
-4 5
-9 0
S ys te m : G m
F req u e nc y (rad /s e c ): 4
P ha s e (de g ): -1 6 5
-1 35
-1 80
-1
10
10
0
10
1
10
2
F r e q u e n c y ( ra d / s e c )
Diagramma di Bode di Gf(s)
B o d e D ia g r a m
40
35
M a g n itu d e ( d B )
30
25
20
15
10
5
P h a s e (d e g )
0
90
60
30
0
10
-3
10
-2
10
-1
10
0
F r e q u e n c y ( ra d / s e c )
10
1
10
2
10
3
Bozza soluzione esercitazione n° 3 di Elementi di analisi dei sistemi
Composizione diagrammi di Bode
B o d e D ia g r a m
40
20
G f( s )
K
M a g n itu d e ( d B )
0
c
Km
-2 0
-4 0
F(s)
-6 0
G
-8 0
m
(s )
-1 00
-1 20
-1 40
90
P h a s e (d e g )
45
0
-4 5
-9 0
-1 35
-1 80
-3
10
10
-2
10
-1
10
0
10
1
10
2
10
F r e q u e n c y ( ra d / s e c )
Risposta alla sollecitazione impulsiva
Im p u ls e R e s p o n s e
0 .6
0 .4
0 .2
a s s e s ta m e n t o
rip o s o
A m p lit u d e
0
-0 .2
-0 .4
-0 .6
c o n tr a z io n e r a p id a
-0 .8
0
1
2
3
4
T im e (s ec )
5
6
7
8
3