V - Gino Giusi

Contenuti del corso
Parte I: Introduzione e concetti fondamentali
richiami di teoria dei circuiti
la simulazione circuitale con SPICE
elementi di Elettronica dello stato solido
Parte II: Dispositivi Elettronici
il diodo a giunzione
transistori ad effetto di campo (FETs)
il transistore bipolare (BJT)
Parte III: Circuiti amplificatori a transistori discreti
amplificatori a BJT e FETs
Il transistore bipolare (BJT)
Il BJT (Bipolar Junction Transistor) è un dispositivo a tre terminali costituito
dall’adiacenza di due giunzioni pn. Sono quindi possibili due configurazioni:
transistore PNP
E
transistore NPN
C
p
emettitore
C
n
collettore
JBE: giunzione
base-emettitore
E
p
n
base
JBC: giunzione
base-collettore
B
p
emettitore
collettore
JBE: giunzione
base-emettitore
C
base
n
p
E
B
C
p
B
n
n
B
p
n
E
JBC: giunzione
base-collettore
Il transistore bipolare (BJT)
Primo dispositivo a stato solido di ampio successo
commerciale a causa del processo di fabbricazione più
semplice e affidabile rispetto a quello dei MOSFETs.
• inventato alla fine dei ‘40 da Bardeen, Brattain e Shockley (Nobel nel ‘56) ai Bell Labs.
• reso disponibile nel ’52 dietro una licenza di 25000$
• il primo BJT al silicio fu sviluppato presso la Texas da Gordon Teal
• la Tokyo Tsushin Kogyo compra la licenza del transistor e nel ‘55 diventa la SONY.
• alla fine dei ‘50 inizia la produzione di massa di radio a BJT
• all’inizio dei ‘60 vengono realizzati i primi IC basati su BJTs
Anche se il MOSFET rappresenta oggi la tecnologia
dominante degli IC, il BJT è largamente utilizzato in
applicazioni ad alte frequenze e ad alte correnti.
Il transistore bipolare (BJT)
• il BJT sembra costituito semplicemente da due giunzioni pn.
• se la larghezza della regione di base è sufficientemente piccola (tipicamente
0.1 µm-100µm), le due giunzioni interagiscono.
•4 regioni di funzionamento in funzione delle 4 possibili combinazioni sullo
stato delle 2 giunzioni.
Il transistore bipolare (BJT)
• nella principale regione di funzionamento, detta regione attiva (JBE-ON, JCB-OFF), l’E
inietta elettroni nella regione di B. La maggior parte vengono raccolti dal C, mentre una
minoranza (se la base è stretta) si ricombinano in base e generano la IB.
• il rapporto IC/IB è molto alto se la base è stretta e il BJT può essere usato come
amplificatore.
• la base agisce come terminale di controllo, modulando la frazione di elettroni raccolti
dal collettore. Il BJT è un dispositivo controllato in corrente (di base), a differenza dei
FETs che sono controllati in tensione (gate-source). Mentre iG = 0, iB è significativa.
Il transistore bipolare (BJT)
• a differenza dei FETs in cui la conduzione è unipolare, ovvero dovuta principalmente
ad un solo tipo di portatore (elettroni negli nFETs, lacune nei pFETs), nei BJT la
conduzione avviene in modo bipolare.
• il funzionamento è basato sul trasporto dei minoritati nella base e quindi i BJT npn
sono preferiti ai pnp a causa della maggiore mobilità degli elettroni rispetto alle lacune.
• struttura non simmetrica: per massimizzare il numero di portatori raccolti dal
collettore l’emettitore è più drogato del collettore
Il modello di Ebers-Moll (npn)
•αF,αR <1: modellizzano
l’effetto
reciproco
delle
giunzioni
I
•il BJT non è simmetrico:
emettitore più drogato del
collettore αR<αF
I
F
=
0.95<αF<1
0<αR<0.95
•IS : corrente di saturazione
I
R
=
IS
α
F
IS
α
R


e
− 1




 VVBC

 e T − 1




V BE
VT
S
α
R
I
S
α
F
10-18A≤ IS≤10-9 A
• il modello DC è definito completamente da 3 parametri (IS, αF, αR)
Il modello di Ebers-Moll (pnp)
I
I
I
F
R
V EB

I S  V T
=
e
− 1

α F 

=
I
α
S
R
 VVCB

 e T − 1




S
α
R
I
S
α
F
Il modello di Gummel-Poon (npn)
iBC
i BE
V BE

I S  V T
=
e
− 1

β F 

i BC
V BC

I S  V T
=
− 1
e

β R 

iT= FiBE- RiBC
iBE
• i modelli di Ebers-Moll e Gummel-Poon sono
αR
equivalenti una volta che β F = α F
βR =
1−αF
• αF ≈ 1
1−αR
βF >> 1
• αF> αR βF > βR
• 3 parametri per descrivere completamente il modello in DC (IS, βF, βR)
Il modello di Gummel-Poon (pnp)
i EB
V EB

I S  V T
=
e
− 1

β F 

i CB
V CB

I S  V T
=
e
− 1

β R 

Esempio 1
Problema: Con riferimento al circuito in
figura determinare il punto di lavoro del
bjt caratterizzato dai parametri IS = 10-16 A,
βF = 50, βR = 1.
Soluzione:
VBE =VBB= 0.75 V
VBC = VBB - VCC = 0.75 V-5V = -4.25 V
Utilizzando la rappresentazione di Gummel-Poon
I BE
V BE
 10 − 16 A
I S  V T
=
− 1 =
e


50
βF 

. 75
 0 .00259

e
 = 7 . 53 µA
−
1




V BC
 10 − 16 A  − 4 . 25

I S  V T
 e 0 .0259 − 1  = − 10 −16 A
I BC =
e
− 1 =



β R 
1



I C = β F I BE − β R I BC − I BC = 376 µA
I B = I BE + I BC = 7 . 53 µA
I E = I B + I C = 384 µA
Esempio 2
Problema: Con riferimento al circuito in
figura determinare il punto di lavoro del
bjt caratterizzato dai parametri IS = 10-16 A,
αF = 0.95, αR = 0.5.
Soluzione:
IE = 100 µA
VBC = 0-5V = -5 V
Utilizzando la rappresentazione di Ebers-Moll
C
IR
IF
IF
IC
V BC
 10 −16 A  − 5

I S  V T
 e 0 .0259 − 1  = − 5 ⋅ 10 − 17 A
=
− 1 =
e


0.5 
α R 


= I E + α R I R ≈ I E = 10 − 4 A
V BE


I S  V T
α I
=
e
− 1  → V BE = V T ln  1 + F F

IS
α F 


= − I R + α F I F ≈ α F I F = 95 µA
I B = I E − I C = 5 µA

 = 0 . 71 V

iC
iR
FiF
B
iB
iF
RiR
iE
E
Regioni di funzionamento
Regione attiva diretta (JBE ON, JBC OFF)
modello di EbersEbers-Moll
modello equivalente
a base comune
IC
C
E
IE
B
VCB
IC ≈ α F I F ≈ α F I E
α F ≅< 1 → I C ≅< I E
αF : guadagno di corrente
diretto a base comune
Regione attiva diretta (JBE ON, JBC OFF)
modello di GummelGummel-Poon
modello equivalente
a emettitore comune
VBE ,ON
IC = β F I B
β F >> 1 → I C >> I B
βF : guadagno di corrente
diretto ad emettitore comune
il BJT può essere usato come
amplificatore di segnale (corrente)
Regione attiva inversa (JBE OFF, JBC ON)
modello di EbersEbers-Moll
modello equivalente
a base comune
I E ≈ −α R I R ≈ α R I C
α R < 1 → I E < IC
αR : guadagno di corrente
inverso a base comune
Regione attiva inversa (JBE OFF, JBC ON)
modello di GummelGummel-Poon
modello equivalente
a collettore comune
VBC ,ON
− IE = βRIB
βR > 1 → IE > IB
βR : guadagno di corrente
inverso a collettore comune
• il BJT potrebbe essere usato come
amplificatore
• si preferisce la zona attiva diretta
(β
βF>>β
βR)
• VBC, ON < VBE,ON (E più drogato di C)
Regione di interdizione (JBE OFF, JBC OFF)
modello di EbersEbers-Moll
IB ≅ 0
IC ≅ 0
IE ≅ 0
poiché tutte le correnti sono nulle il BJT si
comporta da circuito aperto tra C ed E
Regione di saturazione (JBE ON, JBC ON)
modello di Gummel
Gummel--Poon
• poiché le due giunzioni sono polarizzate
in
diretta,
esse
possono
essere
modellizzate
con
una
caduta
costante(VBE,SAT>VBE,ON,VBC,SAT>VBC,ON)
• a causa del diverso drogaggio di E e C le
VON
sono
leggermente
diverse
(VBE,SAT>VBC,SAT)
iC = β F iBE − (β R + 1)iBC

β F iB = β F iBE + β F iBC
in sat. iBE ,iBC > 0 → β F iB > iC
•VCE,SAT=VBE,SAT - VBC,SAT >≈ 0 quindi il
BJT è approssimabile ad un cortocircuito tra C ed E
•le correnti ai terminali sono determinate
dal circuito esterno: aumenti di IB non
risultano in aumenti di IC.
Riferimenti di corrente a BJT
VCC
rete di
polarizzazione
RL
RB
VBB
RE
VEE
• in zona attiva la corrente sul carico RL è costante
• se VBB>0, VEE≥0
VCC > 0 (cond. necessaria)
• se RL ha bisogno del riferimento a massa (VCC=0)
VBB<0, VEE<0 (cond. necessaria)
• per evitare tensioni negative è possibile usare
riferimenti con PNP
il BJT come driver di corrente
•la max corrente erogabile dalla sorgente è VS/RS
•la corrente ILED è limitata da RS
• IB<<IC=ILED
I LED
VS − VLED
=
RS
VS deve erogare poca corrente
• la corrente ILED è fornita
da VCC e non da VS
I LED =
VCC − VLED − VCE
RC
• Q1 tipicamente si polarizza in saturazione:
la più bassa VCE consente di avere una più
bassa VCC (minore potenza dissipata)
la VCE non dipende da βF
il BJT come driver di corrente
Problema: dimensionare RB e RC in modo che ILED=20mA,
IS,max=0.5mA
DATI: VS=5V, RS=5kΩ, VCC=10V, VLED,ON=1.1V
Q1: (βF=100,VBE,SAT=0.8V, VCE,SAT=50mV)
Hp Q1: SAT, D ON
I LED
βF
< IB =
VS − VBE , SAT
I S ,max
VS − VBE , SAT
RB + RS
− RS ≤ RB <
≤ I S ,max
β F (VS − VBE , SAT )
3.4kΩ ≤ RB < 16.25kΩ
RC =
VCC − VLED ,ON − VCE , SAT
I LED
I LED
− RS
Es: RB=4.7 kΩ
= 442.5Ω
Hp OK
Il BJT come interruttore
• in interdizione il bjt si comporta come un interruttore aperto tra C ed E
• in saturazione il bjt si comporta come un interruttore chiuso tra C ed E
C
C
B
B
E
E
• il bjt si comporta come un interruttore controllato dalla corrente di
la quale agisce come terminale di controllo
base,
• a differenza dei FETs dove IG=0, nel caso del BJT è necessario spendere
potenza (IB≠0) per il controllo (maggiore potenza dissipata in applicazioni
digitali).
Regioni di funzionamento
Caratteristiche IV del BJT
caratteristica di uscita ad
emettitore comune
I C = f (V CE , I B )
IC
caratteristica di uscita a
base comune
I C = f (V CB , I E )
caratteristica di trasferimento
I C = f (V BE , V BC
C
E
)
IE
B
VCB
Caratteristiche IV di uscita a emettitore comune
I C = f (V CE , I B )
•iB = 0: BJT OFF
•vCE > vBE (vBC<0), iB >0 : regione attiva diretta, iC = βF iB (indipendente da vCE)
•vCE < vBE (vBC>0), iB >0 : saturazione (il valore limite vBE tra saturazione e
regione attiva aumenta leggermente all’aumentare di iB )
•vCE < 0 : i ruoli di collettore e emettitore si invertono
Caratteristiche IV di uscita a base comune
I C = f (V CB , I E )
• vCB > 0, iE >0: regione attiva diretta, iC ≈ iE è indipendente dalla tensione
• vCB < 0, iE >0: il diodo base collettore viene polarizzato direttamente e iC
cresce esponenzialmente (in direzione negativa) non appena il diodo basecollettore entra in conduzione (saturazione)
Caratteristica di trasferimento a emettitore comune
I C = f (V BE , V BC
)
Es:
I
C
(V BC
 VVBE

T

= 0) = I
− 1
e
S



stessa forma dell’equazione di un
diodo.
transconduttanza
dI
g
m
=
C
I
= C
V
dV
BE Q
T
BJT reali : resistenze serie
Problema: Con riferimento al circuito in
figura determinare il punto di lavoro del
bjt caratterizzato dai parametri IS = 10-16 A,
βF = 50, βR = 1.
Soluzione:
VBE =VBB= 10 V
VBC = VBB - VCC = 0.75 V-5.00V = -4.25 V
Utilizzando la rappresentazione di Gummel-Poon
I BE
V
 10 −16 A
I S  VBET
=
e
− 1 =

β F 
50

10
 0 .0259

e
 = 10 150 A! !!!
−
1




10V
BJT reali : resistenze serie
C
• come nel diodo, è necessario tenere in
considerazione la resistenza delle regioni
neutre
• le correnti ai terminali devono attraversare
regioni di lunghezza non trascurabile per
arrivare nelle zone attive del dispositivo
RC
iC
iBC
B
RBB’
FiBE- RiBC
iB
iBE
RE
iE
E
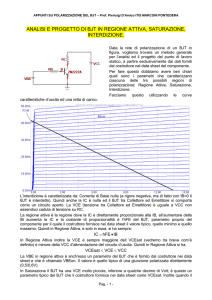
BJT reali : effetto Early
In zona attiva al crescere di VCE lo spessore della SCR di JBC aumenta e lo
spessore della base diminuisce (modulazione dello spessiore di base)
Le IV di uscita hanno una pendenza positiva
nella regione attiva diretta la IC (βF) non è
indipendente da VCE


V
CE
1 +

β ≈β
F
FO 
V

A 
Tensione di Early (VA=10÷150V): le IV di uscita sono estrapolate fino al
punto in cui IC è uguale a zero.
Modello SPICE per il BJT
Sintassi:
Q<name> < collector node> <base node> <emitter node>
+ [substrate node] <model name> [area value]
.MODEL <model name> NPN [model parameters]
.MODEL <model name> PNP [model parameters]
Esempio:
Q1 1 2 3 BC107 10
.MODEL BC107 NPN BF=30
BJT: modello in continua (Gummel-Poon)
I BE =
I BC
I CC
βF
VBE


IS  NF⋅VT
e
=
− 1

BF 

I CT = (I CC − I EC ) / Kqb
VBC


I EC
IS  NR ⋅VT
=
=
e
− 1

β R BR 

I GRE
VBE
 NE

⋅VT

= ISE e
− 1




VBC
 NC

⋅
V
I GRC = ISC e T − 1




NK
Kqb = Kq1 1 + (1 + 4 Kq 2 ) / 2
Kq1 = 1 / (1 − VBC / VAF - VBE / VAR )
[
]
Kq 2 = β F I BE / IKF + β RI BC / IKR
•RBB’, RC, RE: resistenze di accesso
• IGRE, IGRC : correnti dovute a
fenomeni di G-R nelle regioni
svuotate
• Kqb: parametro che tiene conto di
effetti reali tra cui l’effetto Early
BJT: modello in continua
BJT: modello per ampi segnali
I CT = (I CC − I EC ) / Kqb
Esempio
Problema: simulare le caratteristiche di uscita di un BJT npn (parametri IS =
10-16 A, βF = 50, βR = 1) nell’intervallo 0≤VCE≤15V, per 0 ≤ IB≤ 10µA.
caratteristiche di uscita bjt npn
1
IB 2 0 DC 0
VCE 1 0 DC 0
Q1 1 2 0 bjtmodel
.MODEL bjtmodel NPN BF=50 BR=1
+IS=1e-16
.DC VCE 0 15 0.1 IB 0 1e-5 1e-6
.PROBE IC(Q1)
.END
2
Q1
IB
0
VCE
Analisi in DC di circuiti con BJT
RC
risoluzione analitica
IC
VCC
RB
VBB
IB
V BB = R B I B + V BE
V = R I + V
 CC
C C
CE

 I C = f (V BE , V CE )
 I B = g (V BE , V CE )
risoluzione grafica (nota IB)
risoluzione analitica
V CC = R C I C + V CE

 I C = f (V BE , V CE )
Analisi in DC di circuiti con BJT
RC
risoluzione analitica
IC
VCC
RB
VBB
IB
V BB = R B I B + V BE
V = R I + V
 CC
C C
CE

 I C = f (V BE , V CE )
 I B = g (V BE , V CE )
risoluzione approssimata
risoluzione analitica
V CC = R C I C + V CE

 I C = f (V BE , V CE )
1. ipotesi su f, g (OFF, attiva diretta, attiva
inversa o saturazione)
2. si risolve il circuito e si determina Q
3. si verifica l’ipotesi 1
Analisi in DC di circuiti con BJT: Esempio
Problema: Calcolare il punto di lavoro di Q.
Dati noti: VBB= 3V, VCC=5V, RB=1MΩ, RC=1kΩ,
Q: (βF = 100, βR = 1, VBE,ON=0.7, VBC,ON=0.5, VCE,SAT=0.2V)
Soluzione: VCC e VBB tendono a pol. dir. JBE
VBB tende a pol. dir. JBC, VCC tende a pol.
inv. JBC
Hp ZONA ATTIVA
(VBE=VBE,ON=0.7V, IC=βFIB)
IB =
3 − 0 .7
V BB − V BE
= 2 . 3 µA
=
10 3
RB
I C = β F I B = 230 µA
V BC = V BE − V CC + R C I C = − 4 . 53 V
I E = I B + I C = 232 . 3 µA
 I B = 2 . 3 µA ≥ 0
Hp OK

V BC = − 4 . 53 V ≤ V BC ,ON = 0 . 5 V
RC
IC
VCC
RB
VBB
IB