proprietà della derivata

proprietà della derivata ­ punti stazionari PROPRIETA' DELLA FUNZIONE DERIVATA
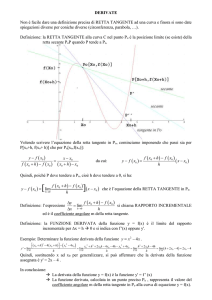
Data una funzione y=f(x) e la sua funzione derivata y '=f '(x).
La derivata per definizione esprime la pendenza della funzione in ogni suo punto.
Ad esempio se y=f(x)=x3­5x+1 e y '=f '(x)=3x2­5
la pendenza della funzione in x=2 è y'= f '(2) = 3(2)2­5 = 7
la pendenza della funzione in x=­1 è y'= f '(­1) = 3(­1)2­5 = ­2
graficamente la pendenza si rappresenta come il coefficiente angolare della retta tangente
1
­2
7
1
y=x3­5x+1 Da questi risultati si può ricavare che
nei punti in cui la derivata è positiva l'andamento della funzione è crescente
nei punti in cui la derivata è negativa l'andamento della funzione è decrescente
Studiando quindi il segno della derivata possiamo ricavare le seguenti informazioni
se y'=f '(x)<0 allora y=f(x) è decrescente
se y'=f '(x)>0 allora y=f(x) è crescente
se y'=f '(x)=0 allora y=f(x) si mantiene orizzontale
1
proprietà della derivata ­ punti stazionari PUNTI STAZIONARI ( pag.194)
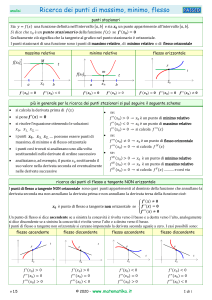
Data una funzione y=f(x), un punto x0 si dice stazionario se f '(x0) =0 . I punti stazionari possono essere di quattro tipi in base al segno della funzione derivata nell'intorno del punto x0:
1° caso: x0 è un punto di massimo
x0
segno di f '(x)
­
+
si dispone
la funzione f(x) : cresce in modo
orizzontale
decresce
x0 è un punto di massimo
2° caso: x0 è un punto di minimo
x0
segno di f '(x)
­
la funzione f(x) : decresce
+
si dispone
in modo
orizzontale
cresce
x0 è un punto di minimo
3° caso: x0 è un punto di flesso ascendente
x0
segno di f '(x)
+
la funzione f(x) : cresce
+
si dispone
in modo
orizzontale
cresce
x0 è un punto di flesso a tangente orizzontale ascendente
4° caso: x0 è un punto di flesso discendente
x0
segno di f '(x)
­
la funzione f(x) : decresce
­
si dispone
in modo
orizzontale
decresce x0 è un punto di flesso a tangente orizzontale discendente
2
proprietà della derivata ­ punti stazionari ESEMPI DI STUDIO DI FUNZIONI CON IL SEGNO DELLA DERIVATA
y=(x+1)3
1) dominio D: (­∞;+∞)
2) intersezioni con gli assi: A(­1;0) e B(0;1)
3) segno: x> ­1
4) lim y = ­∞
x ­∞
5) y'=3(x+1)2
lim y = +∞
x +∞
B
­1
+
segno di f '(x)
A
+
x=­1 è un punto di flesso a tangente orizzontale ascendente
y=x4­2x3
1) dominio D: (­∞;+∞)
2) intersezioni con gli assi: A(0;0) e B(2;0)
3) segno: x3(x­2)>0
4) lim y = +∞
lim y = +∞
x ­∞
x +∞
2
2
3
(2x­3)
5) y'=4x ­6x =2x
0
segno di 2x2
segno di 2x­3
segno di f '(x)
+
­
­
3/2
+
­
­
x=0 è un punto di flesso a tangente orizzontale discendente
+
+
+
x=3/2 è un punto di minimo
B
A
minimo
3 ; ­ 27
2 16
3