caricato da
lucia.minchielli
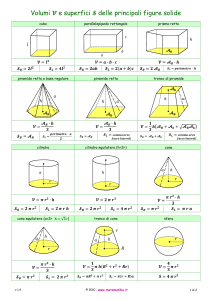
Poliedri Platonici: Geometria e Storia

15/02/23, 18:21 www.manuelacasasoli.altervista.org/pagine/matematica/poliedri_platonici.html I cinque poliedri platonici I "magnifici sette" della classe 3a C (2011-2012) di Casacastalda vogliono saperne di più sui poliedri regolari. Chiedono, infatti, a gran voce: "Perché sono solo cinque?" Come al solito la curiosità di questi bravi ragazzi non è sempre soddisfatta dai loro libri di testo!!! Un poliedro è regolare quando tutte le sue facce sono poligoni regolari uguali e in ogni vertice insiste lo stesso numero di spigoli. Gli antichi greci avevano già scoperto che di poliedri regolari ce ne sono solo cinque, chiamati poliedri platonici. Tre di questi hanno come facce dei triangoli equilateri, : il tetraedro (4 facce), l'ottaedro (8 facce) e l'icosaedro (20 facce). Uno solo ha 6 facce quadrate, il cubo o esaedro, mentre l'ultimo, il dodecaedro, ha 12 facce costituite da pentagoni regolari. Tutti possono essere inscritti in una sfera, nella quale tutti i vertici giacciono sulla superficie della sfera stessa. www.manuelacasasoli.altervista.org/pagine/matematica/poliedri_platonici.html 1/3 15/02/23, 18:21 www.manuelacasasoli.altervista.org/pagine/matematica/poliedri_platonici.html Nella Grecia classica ognuno di questi poliedri veniva associato ad uno degli elementi naturali. Il cubo rappresentava la Terra; il tetraedro il fuoco; l'ottaedro l'aria, l'icosaedro l'acqua e il dodecaedro era il simbolo del cosmo, dell'Universo preso nella sua totalità, come disse Platone: "La divinità lo utilizzò per tessere le costellazioni per tutto il cielo". La grande attrazione che gli antichi greci, e soprattutto i pitagorici, provavano nei confronti dei poliedri derivava probabilmente dall'osservazione di minerali cristallizzati, molto diffusi nella Magna Grecia, come ad esempio gli spettacolari cristalli di pirite a forma di dodecaedro. Cristalli di pirite. (http://farm7.static.flickr.com/6176/6258830343_3eaf032dbe.jpg) Ora cerchiamo di capire perché questi poliedri regolari sono solo cinque. In ogni poliedro la parte di spazio compresa tra gli angoli delle facce che hanno un vertice in comune si chiama angoloide. L'angoloide è formato da almeno 3 facce, perché altrimenti non si chiude. Inoltre la somma degli angoli con il vertice in comune deve essere minore di 360°. Se fosse, infatti, maggiore o uguale a 360°, l'angoloide "si schiaccerebbe" sul piano o addirittura si "ribalterebbe" come un ombrello. In un poliedro regolare gli angoloidi sono tutti congruenti, quindi ciascuno di essi deve essere formato da almeno tre facce che sono poligoni regolari e tali che la somma degli angoli con il vertice in comune www.manuelacasasoli.altervista.org/pagine/matematica/poliedri_platonici.html 2/3 15/02/23, 18:21 www.manuelacasasoli.altervista.org/pagine/matematica/poliedri_platonici.html sia minore di 360°. Ora potete cominciare a riflettere... Supponiamo che le facce del poliedro regolare siano triangoli equilateri: l'ampiezza dell'angolo di una faccia è di 60°...Allora con tre facce per vertice (3 x 60 = 180°) si ottiene un tetraedro, con quattro facce per vertice (4 x 60 = 240°) si ottiene un ottaedro e infine con cinque facce per vertice (5 x 60 = 300°) si ottiene un icosaedro. Non si possono avere sei facce per vertice perché la somma degli angoli per vertice sarebbe uguale a 360° e l'angoloide si schiaccerebbe sul piano. Ora provate voi... Se la faccia è un quadrato: 3 x 90° = ......... Chi è? E 4 x 90° = ......... Esiste? Se la faccia è un pentagono regolare: 3 x 108° = ......... Chi è? E 4 x 108° = ........ Esiste? Se la faccia è un esagono regolare: 3 x 120° = ......... Esiste? Quanti sono i poliedri regolari che siete riusciti ad ottenere? Perché, allora, non possono esistere poliedri regolari delimitati da poligoni regolari con un numero di lati superiore a cinque? Buon divertimento!!! Referenze M. Zarattini (2010) "Matematica intorno a te". Quaderno operativo 3. Edizioni Scolastiche Bruno Mondadori. Fernando Corbalàn (2011) La sezione aurea. Il linguaggio matematico della bellezza. Mondo Matematico. RBA Italia S.r.l. Ciao, Manuela ([email protected]). www.manuelacasasoli.altervista.org/pagine/matematica/poliedri_platonici.html 3/3