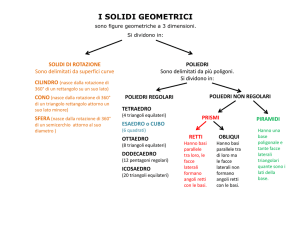
POLIEDRI REGOLARI
- PLATONICI -
Proclo, storico della matematica del V secolo dopo Cristo, legato alla filosofia neo-platonica,
attribuisce a Pitagora la scoperta dei 5 poliedri regolari, ma la mancanza di frammenti attribuibili a
Pitagora rende difficilmente dimostrabile questa tesi.
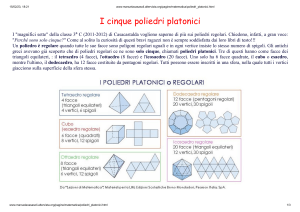
Nel Timeo di Platone, di poco successivo a Pitagora, troviamo una descrizione precisa dei 5 corpi
regolari, cioé dei possibili solidi sfaccettati che abbiano le facce, gli spigoli e gli gli angoli, uguali
tra loro. Platone userà questa straordinaria scoperta come simbologia dell'universo e dei suoi
elementi base:
il fuoco (tetraedro)
la terra (cubo)
l'aria (ottaedro)
l'acqua (l'icosaedro)
il quinto poliedro regolare, il dodecaedro, era a simboleggiare la quinta essenza che tutto
avvolge e comprende.
La dimostrazione che sono possibili al massimo 5 corpi regolari si trova anche nel Timeo di Platone
(e in tutti i testi di divulgazione su questo argomento) e non è difficile: dato che in ogni vertice del
poliedro si deve creare un angoloide, ci vogliono almeno tre facce ed in più deve accadere che la
somma degli angoli delle facce che concorrono a quel vertice deve essere minore di 360 gradi;
in caso contrario infatti le facce si appiattirebbero in uno stesso piano.
Per comprendere che i poliedri regolari sono solo 5, dobbiamo conoscere l’ampiezza degli angoli
dei poligoni regolari:
triangolo equilatero
60°
quadrato
90°
pentagono regolare
108°
Si = 180°x (5-2) =180°x3 = 540°
α = 540° : 5 = 108°
esagono regolare 120°
Si = 180°x (6-2) =180°x4 = 720°
α = 720° : 6 = 120°
Questo implica che non è possibile avere facce esagonali o con un numero
maggiore di lati dato che questi poligoni hanno angoli maggiori di 120°.
Restano dunque possibili solo 5 casi:
3 facce pentagonali concorrenti in un vertice (108ox3= 324o< 360o)
3 facce quadrate concorrenti in un vertice (90ox3=270o<360o)
3 facce triangolari concorrenti in un vertice (60ox3=180o<360o)
4 facce triangolari concorrenti in un vertice(60ox4=240o<360o)
5 facce triangolari concorrenti in un vertice(60ox5=300o<360o)
Non è possibile avere in angoloide con facce esagonali perché 120°x3= 360°
Si vede quindi facilmente che non possono esistere più di 5 poliedri regolari.
L'effettiva costruzione di questi poliedri, che è patrimonio distintivo della cultura scientifica
occidentale, si trova nel tredicesimo libro degli Elementi di Euclide e rappresenta in un certo senso
il punto di arrivo della geometria classica. Queste costruzioni nei libri di divulgazione sono
generalmente omesse, trascurando in questo modo proprio gli aspetti più ingegnosi e stimolati della
geometria euclidea.
Una delle possibili costruzioni dell’ICOSAEDRO