1 - I numeri complessi

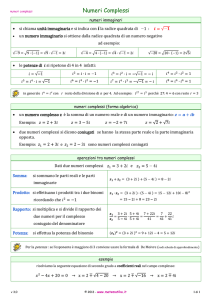
1 – I numeri complessi
http://www.sandroronca.it/matematica/NumeriComplessi/NumeriComplessi1.html
1. I numeri complessi
Vedremo definizioni e proprietà di una importante categoria di numeri inizialmente introdotta per
risolvere il problema dell’estrazione di radici quadrate di numeri negativi e rivelatasi uno strumento
matematico potentissimo per la descrizione dei fenomeni fisici e lo sviluppo stesso della
Matematica.
Introduzione e cenni storici
La prima fugace comparsa dei numeri complessi avviene nella prima metà del XVI secolo. In Italia
Gerolamo Cardano (1501, 1576), poliedrico medico e matematico, trattando del metodo della falsa
posizione, propone un problema, manifestamente impossibile (Ars Magna o Artis Magnae, 1545):
“ Dividi 10 in due parti che moltiplicate tra loro diano 40 “, che possiamo anche enunciare così:
“ trovare due numeri x , y tali che x + y = 10 e x  y = 40 “.
Seguiamo il ragionamento di Cardano. Facendo riferimento alla figura, immaginiamo che il
segmento ab sia lungo 10 (non importa l’unità di misura), il quadruplo di ab , che possiamo
rappresentare con il rettangolo tratteggiato, vale 40 .
Il punto c divide ab in due parti x , y il cui prodotto deve dare 40 .
Inizialmente (falsa posizione) Cardano fa coincidere c con il punto medio di ab e quindi
x = y = x0 = 5 . L’area del rettangolo ad (così lo identifica), che in questo caso è un quadrato, è pari
a xy = 𝑥02 = 25 , ovviamente diversa da 40.
La soluzione, se esiste, si può ottenere solo spostando c di una quantità r dalla posizione iniziale,
ma è chiaro che se, ad esempio, x diminuisce di r , allora y dovrà aumentare della stessa quantità,
cioè se x = x0 - r allora y = x0 + r . Questo perché la somma x + y deve essere uguale alla
lunghezza di ab (10).
Se x = x0 - r e y = x0 + r sono la suddivisione cercata, dovrà essere vero che (x0 - r) (x0 + r) = 40 ,
nel caso specifico (5 - r) (5 + r) = 40 . Svolgendo il prodotto notevole si ha 25 - r2 = 40 , che
implica la negatività di r2 : r2 = - 15 .
A questo punto Cardano introduce la quantità √−15 (“ ideo immaginaberis R. m. 15 “, nel testo e
con la notazione di allora), da sottrarre e aggiungere a 5 per avere la soluzione cercata:
“ 5. p. R. m. 15 e 5. m. R. m. 15.” che significa 5 + √−15 e 5 - √−15 . Quindi dimostra che
effettivamente queste entità costituiscono una soluzione del problema, dato che
5 + √−15 + 5 - √−15 = 10
,
(5 + √−15) (5 - √−15) = 52 - (√−15))2 = 25 - (-15) = 40 .
Giordano però non riesce a trovare una giustificazione per queste strane quantità. Ne attribuisce la
comparsa alla diversa natura di ad (il quadrato), che non è la stessa di 40 (che considera una linea):
“ essendo una superficie più lontana dal numero e una linea più vicina ad esso “. Alla fine, non
riconoscendo il “ tesoro matematico “ che aveva a portata di mano, ritiene questi ragionamenti
essere capziosi (sofistici) e tanto sottili quanto inutili.
Radici quadrate negative comparivano anche nelle formule risolutive di alcune equazioni di terzo
grado, ad esempio x3 - 15x = 4 , di cui si conosceva, per sostituzione diretta, la radice reale x = 4 .
3
3
La formula risolutiva di Dal Ferro dava x = √2 + √−121 + √2 − √−121 .
Raffaele Bombelli (1526-1573) cercò di dare alle radici cubiche della formula precedente
un’espressione formalmente simile a quella dei radicandi, quindi del tipo a  √−𝑏 . Secondo la
notazione moderna deve essere allora (a + √−𝑏)3 = 2 + √−121 e (a - √−𝑏)3 = 2 - √−121 .
Sapendo che si deve avere x = 4 , si può facilmente dimostrare che x = 2 + √−1 + 2 – √−1 .
Descartes (Cartesio, 1596-1650) per primo chiamò “ numeri immaginari “ entità quali √−121 o
√−1 ed Eulero (1707-1783) nel 1777 introdusse il simbolo “ i “ per designare la radice quadrata di
-1 , i = √−1 .
Ciò che sembrava quasi un incidente matematico, qualcosa in cui non credere veramente (numeri
immaginari in contrapposizione con i numeri reali), si è poi rivelata una delle più feconde scoperte
della Matematica. Accade spesso così. I numeri complessi, le strutture e i concetti matematici che
da essi derivano sono ora uno strumento irrinunciabile per la conoscenza scientifica e per la stessa
Matematica.
Numeri immaginari
Se nel campo (in Algebra è una particolare struttura dotata delle proprietà di un anello
commutativo, ovvero di un insieme in cui sono definite somma e moltiplicazione, e sono valide la
legge associativa e commutativa oltre all’esistenza del reciproco di ogni elemento diverso da zero)
dei numeri reali tentiamo di risolvere equazioni come x2 + 1 = 0 andiamo incontro ad una difficoltà
insormontabile: l’equazione può essere scritta come x2 = -1 , ma sappiamo che non esiste alcun
numero reale il cui quadrato sia negativo.
Non siamo in grado di eseguire l’operazione di estrazione di radice quadrata di numeri negativi in
campo reale, per cui una soluzione come x = √−1 viene considerata priva di senso. Per molto
tempo si è evitato il problema semplicemente ammettendo che l’equazione x2 + 1 = 0 non possiede
soluzioni in campo reale.
Il problema viene risolto introducendo la quantità i = √−1 (in alcuni casi, ad esempio in
elettrotecnica ed in elettronica, per evitare confusione con il simbolo dell’intensità di corrente, si
preferisce utilizzare il simbolo “ j “) detta “ unità immaginaria “.
Una prima evidente proprietà dell’unità immaginaria è la seguente:
i2 = i  i = (√−1)2 = - 1 .
Conseguentemente abbiamo che:
i3 = i  i  i = - i
,
i4 = i  i  i  i = 1 .
Più avanti vedremo una interpretazione geometrica di questi risultati.
Le soluzioni della precedente equazione sarebbero allora x1 = + i e x2 = - i .
x2 + 4 = 0 , ad esempio, darebbe come soluzioni x1 = + 2i e x2 = - 2i .
Oggetti di questo tipo prendono il nome di numeri immaginari e sono formati dal “ prodotto “ di un
numero reale per l’unità immaginaria stessa.
In realtà per affermare che si tratta di numeri bisogna provarlo, cioè si deve verificare che siano
soddisfatte le proprietà tipiche dei numeri, in particolare deve essere possibile definire le operazioni
che si possono eseguire tra numeri, tra cui, ovviamente, somma e prodotto. Possiamo creare nuovi
numeri immaginari sommando (o sottraendo) ripetutamente i a sé stessa: i + i + i = 3i , o
5
moltiplicando i per un numero reale: 2,718 i , - i , - √2 i , ecc.
3
In generale sarà possibile sommare due numeri immaginari applicando le regole algebriche (nel
caso di generalizzazioni si cerca di applicare regole e definizioni già utilizzate per altri tipi di
numeri) per i monomi, così 2i + 3i = 5i . Analogo discorso per la moltiplicazione, tenendo presente
la proprietà di i prima enunciata: 2i  3i = 6i2 = 6 (-1) = -6 .
Dunque il prodotto di due numeri immaginari è sempre un numero reale, ciò significa che l’insieme
dei numeri immaginari non è chiuso rispetto alla moltiplicazione (il risultato non è più un numero
immaginario). Questa situazione rende necessaria la generalizzazione che porta alla definizione di
“ numero complesso “.
Somma, differenza e prodotto
Possiamo sommare numeri reali e numeri immaginari, ottenendo oggetti del tipo a + i b (oppure
a + j b). Per queste entità definiamo somma, prodotto e differenza sulla scorta di quanto fatto in
algebra per i binomi (nel caso di generalizzazioni si cerca di applicare regole e definizioni già
utilizzate per altri tipi di numeri), ricordando la proprietà di i prima enunciata.
Somma:
(a + i b) + (c + i d) = (a + c) + i (b + d)
Differenza:
(a + i b) - (c + i d) = (a - c) + i (b - d)
Prodotto:
(a + i b)  (c + i d) = (ac - bd) + i (ad + bc)
Con queste definizioni è possibile dimostrare che oggetti matematici come a + i b godono
effettivamente di tutte le proprietà caratteristiche dei numeri e quindi sono da considerarsi numeri a
tutti gli effetti. Essi prendono il nome di numeri complessi.
Il numero a (oppure c) è detto “ parte reale “ del numero complesso, mentre b (oppure d) è la
“ parte immaginaria “. Se z = a + i b , allora Re(z) = a , Im(z) = b .
Notiamo che per indicare un numero complesso utilizziamo un carattere tipografico in grassetto, z ,
oppure 𝑧̇ , carattere puntato.
Esiste un numero complesso che sommato a qualsiasi numero complesso z = a + ib dia il numero
z stesso? Si, è il numero 0 = 0 + i 0 , infatti (a + i b) + (0 + i 0) = (a + 0) + i (b + 0) = a + i b .
Questo numero è l’elemento neutro per la somma di numeri complessi.
Esiste un numero complesso che moltiplicato per qualsiasi altro numero complesso z = a + i b dia
il numero z stesso? Si, è il numero 1 = 1 + i 0 , infatti
(a + i b)  (1 + i 0) = (a  1 - b  0) + i (a  0 + b  1) = a + i b .
Il numero 1 = 1 + i 0 è l’elemento neutro per il prodotto di numeri complessi.
Numeri complessi coniugati
Abbiamo appena visto che i 2 = i  i = -1 e di conseguenza che i  (-i) = 1 : il risultato è un numero
reale positivo. Ciò si verifica per qualsiasi prodotto di numeri immaginari, ad esempio
i 7  (-i 7) = - i 2 49 = 49 .
Numeri di questo tipo si dicono numeri “ immaginari coniugati “. Differiscono solo per il segno e
moltiplicati tra loro danno sempre un numero reale positivo, che è il quadrato della parte
immaginaria del numero immaginario stesso: i b  (-i b) = b2 .
Generalizzando: a + i b e a - i b sono numeri complessi coniugati. Essi differiscono solo per il
segno della parte immaginaria. Se moltiplichiamo due numeri complessi coniugati otteniamo
(a + i b) (a - i b) = a2 - i ab + i ab - i2 b2 = a2 + b2 .
La radice quadrata di questa grandezza, che è un numero reale sempre positivo, √𝑎2 + 𝑏 2 , è detta
“ modulo “ del numero complesso:
|a| = |a + i b| = √𝑎2 + 𝑏 2 .
Se z = a + ib , indichiamo il suo complesso coniugato con 𝒛 = a - i b . Avremo quindi
z = |z| = √𝒛  𝑧 = √𝑎2 + 𝑏 2 .
A volte il modulo è indicato con la lettera “ r “: |z| = r = √𝑎2 + 𝑏 2 .
Divisione
𝑎+𝑖𝑏
Dovendo eseguire ad esempio l’operazione
per evitare la complicazione di un denominatore
𝑐+𝑖𝑑
complesso, si sfrutta la proprietà dei complessi coniugati e si assume che una frazione complessa
(come una frazione algebrica) non cambi moltiplicando numeratore e denominatore per lo stesso
numero (complesso). In questo caso moltiplicheremo numeratore e denominatore per il complesso
coniugato del denominatore:
𝑎+𝑖𝑏
𝑐+𝑖𝑑
=
𝑎+𝑖𝑏 𝑐−𝑖𝑑
𝑐+𝑖𝑑 𝑐−𝑖𝑑
=
(𝑎𝑐 + 𝑏𝑑) + 𝑖 (𝑏𝑐 − 𝑎𝑑)
𝑐2
+ 𝑑2
=
𝑎𝑐 + 𝑏𝑑
𝑐2
+ 𝑑2
+i
𝑏𝑐 − 𝑎𝑑
𝑐 2 + 𝑑2
,
ottenendo così un denominatore reale, che sappiamo facilmente trattare.
In seguito dimostreremo che è possibile elevare a potenza ed estrarre radice dai numeri complessi e
che valgono tutte quelle proprietà (commutativa, associativa, distributiva) che ci assicurano che i
numeri complessi sono numeri a tutti gli effetti.
Definizione formale di numero complesso
Vediamo adesso una definizione formale di numero complesso.
“ I numeri complessi sono costituiti da coppie ordinate di numeri reali “ .
Tra tali coppie è definita un’operazione somma
(a, b) + (c, d) = (a + c, b + d) ,
e un’operazione prodotto
(a, b)  (c, d) = (ac - bd, ad + bc) .
Date queste definizioni si può facilmente dimostrare che l’elemento neutro per la somma è (0, 0) ,
(a, b) + (0, 0) = (a + 0. b + 0) = (a, b) ,
l’elemento opposto di (a, b) è (-a, -b) ,
(a, b) + (-a, -b) = (a - a, b - b) = (0, 0) ,
l’elemento neutro per la moltiplicazione è (1, 0) ,
(a, b)  (1, 0) = (a  1 - b  0, a  0 + b  1) = (a, b) .
Dimostrazione
Il reciproco di un numero complesso (a, b) , indichiamolo con
1
(𝑎,𝑏)
=(
𝑎
𝑎2
+ 𝑏2
,
−𝑏
𝑎2
+ 𝑏2
1
(𝑎,𝑏)
,è
).
Infatti, detto (a, b) un numero complesso qualsiasi, e (r, s) il suo reciproco, per definizione di
reciproco deve essere (a, b)  (r, s) = (ar - bs, as + br) = (1, 0) .
Per determinare r ed s basta risolvere il sistema
𝑎𝑟 − 𝑏𝑠 = 1
{
𝑎𝑠 + 𝑏𝑟 = 0
ricaviamo r dalla prima equazione e sostituiamola nella seconda
r=
1 + 𝑏𝑠
𝑎
 as + b
s=
1 + 𝑏𝑠
𝑎
−𝑏
𝑎2
+ 𝑏2
=0 
 r=
𝑎2 𝑠
𝑎
1 + 𝑏𝑠
𝑎
+
𝑏 + 𝑏2 𝑠
𝑎
=0 
−𝑏
=
1+𝑏 2
𝑎 + 𝑏2
Possiamo quindi definire l’operazione divisione
𝑎
(𝑎,𝑏)
(𝑐,𝑑)
=
𝑠 (𝑎2 + 𝑏2 ) + 𝑏
𝑎
𝑎2 + 𝑏2 − 𝑏2
𝑎2 + 𝑏2
𝑎
=
= 0  Num = 0 
𝑎
𝑎2
+ 𝑏2
come prodotto (a, b) 
.
1
(𝑐,𝑑)
.
I numeri reali sono tutte le coppie del tipo (a, 0) con parte immaginaria nulla. Tutte le coppie del
tipo (0, b) , cioè con parte reale nulla, rappresentano i numeri immaginari.
Applicando le definizioni:
i 2 = (0, 1)  (0, 1) = (0  0 - 1 1, 0  1 + 1  0) = (-1, 0) = -1 .
Il prodotto di due numeri reali è un numero reale:
(a, 0)  (c, 0) = (a  c - 0  0, a  0 + 0  c) = (ac, 0) = ac .
Il prodotto di due numeri immaginari è un numero reale:
(0, b)  (0, d) = (0  0 - b  d, 0  d + b  0) = (- bd, 0) = - bd .
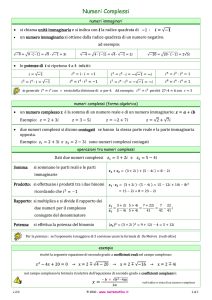
2. La geometria dei numeri complessi
Abbiamo visto come si eseguono le operazioni fondamentali con i numeri complessi, ma questo non
ci fa ancora comprendere quale sia la loro vera potenza. Perciò è opportuno ricorrere ad una loro
rappresentazione geometrica.
Il piano di Argand-Gauss
I numeri reali vengono normalmente rappresentati come punti di una retta, una volta fissata la
posizione dello zero e determinato il verso positivo.
Questa retta viene chiamata retta reale. Ad ogni suo punto (i punti sono infiniti) viene associato,
senza possibilità di ambiguità, uno ed un solo numero reale. Si dice che esiste una corrispondenza
biunivoca tra i numeri reali e i punti della retta.
E’ possibile una rappresentazione analoga per i numeri complessi?
Sorge subito la difficoltà di rappresentare i = √−1 .
Semplicemente non esiste alcun punto della retta a cui associare l’unità immaginaria i , dal
momento che i non è un numero reale.
Se moltiplichiamo 1 per i 2 otteniamo -1 , che è reale ed è rappresentato da un punto sulla retta.
Potremmo dunque pensare che i 2 trasformi 1 nel suo opposto -1 , che geometricamente
corrisponde ad una rotazione di 180° del segmento 0, 1 . In questo senso, moltiplicare 1 per i
potrebbe significare ruotare il segmento 0, 1 di 90° e dunque i = √−1 sarebbe rappresentabile
da un punto su una retta perpendicolare all’asse reale.
Caspar Wessel (1798), Argand (1806) e infine Gauss (1831) ebbero appunto la geniale idea di
rappresentare i , e tutti gli altri numeri immaginari, su di un’altra retta perpendicolare alla retta
reale.
Questa retta prende il nome di retta immaginaria o asse immaginario.
Nel piano di Gauss ogni numero complesso z = a + ib è rappresentato da un punto, identificato da
una coppia ordinata di numeri reali, z = (a, b) in cui il primo elemento della coppia è la parte reale
ed il secondo la parte immaginaria di z . I numeri reali sono rappresentati da tutte le coppie del tipo
(a, 0) , i numeri immaginari da tutte le coppie (0, b) . In particolare l’unità immaginaria i è
rappresentata dalla coppia (0, 1) , quindi i = √−1 = (0, 1) .
Numeri complessi e vettori
Abbiamo evidenziato che il prodotto di un numero complesso per il suo coniugato fornisce una
grandezza reale, sempre positiva, z  𝒛 = a2 + b2 , la cui radice quadrata r = |z| = √𝑎2 + 𝑏 2 abbiamo
chiamato modulo del numero complesso.
Nel piano di Gauss |z| rappresenta la distanza (euclidea) del punto z dall’origine. Questo conduce
a pensare al numero complesso non solamente come ad un punto nel piano di Gauss, ma come ad
un vettore di modulo |z| che rappresenta la posizione del punto z rispetto all’origine degli assi.
Anche qui però dobbiamo fare attenzione al fatto che non basta semplicemente dare un nome ad una
grandezza : se affermiamo che z è un vettore dobbiamo provare che si comporta effettivamente
come un vettore. Ad esempio dovremmo verificare che i vettori rappresentativi di numeri complessi
si sommano secondo la regola del parallelogrammo.
Questo si può facilmente vedere nelle seguenti figure. Dato allora un numero z e un numero w ,
visualizziamo il numero z + w ed i vettori corrispondenti. Anche la differenza d = z - w ha il suo
corrispondente nella differenza tra vettori. Il vettore differenza d è semplicemente il vettore
differenza (tratteggiato) trasposto ed applicato all’origine.
Interpretazione geometrica del prodotto e della divisione di numeri complessi
Sulla pagina del sito è presente una lavagna interattiva. Se visualizziamo il prodotto p = z  w e
teniamo fisso z facendo variare il punto w , si osserva che il vettore p oltre a subire una
variazione del modulo viene ruotato di un certo angolo.
Possiamo evidenziare meglio questo fatto immaginando di vincolare il punto z a muoversi lungo
una circonferenza. Consideriamo un secondo numero w e supponiamo che il suo punto
rappresentativo a sua volta si muova lungo una circonferenza, ciò equivale a far variare z e w
mantenendo costante il loro modulo.
Osserviamo il comportamento del prodotto p = z  w , portiamo w sull’asse reale e notiamo che il
vettore prodotto giace cioè sulla stessa retta di z e quindi forma con l’asse reale un angolo uguale a
quello formato da z (in effetti abbiamo moltiplicato per un numero reale - ndmax)
Ora ruotiamo w ad esempio in senso antiorario: il vettore prodotto ruota anch’esso mantenendo
costante il modulo. Cerchiamo di apprezzare l’angolo tra p e z , confrontiamolo con l’angolo che
w forma con l’asse reale: questi due angoli sono evidentemente uguali.
L’angolo che il vettore rappresentativo di un numero complesso forma con l’asse reale è detto
“ argomento “ del numero complesso. L’argomento  di p allora è la somma tra  , argomento di
z , e  , argomento di w :  =  +  (abbiamo appena visto che  -  =  quindi  =  +  - ndmax).
Se spostiamo w nel quadrante IV questa relazione è ancora vera? Sembrerebbe di dover eseguire
una differenza tra angoli, questo perché l’angolo  in questo caso è negativo: la relazione
 =  +  è quindi ancora valida, e lo è anche per gli altri quadranti.
Siamo nel quadrante IV, la differenza tra p e z è -  +  quindi abbiamo che -  +  = -  ovvero  =  +  .
(ndmax)
Cosa possiamo dire della divisione q =
𝒛
𝒘
?
Anche qui poniamo w sull’asse reale, poi ruotiamo w in senso antiorario: sembra chiaro che
l’angolo  , argomento di q , corrisponde alla differenza tra  e  :  =  -  .
Potremo dimostrare questi fatti dopo aver introdotto la forma trigonometrica dei numeri complessi.
Nella seconda figura abbiamo che l’angolo tra q e z è nullo così come è nullo l’angolo tra w e l’asse reale, dunque
questi due angoli sono uguali. Nella prima figura si nota che l’angolo tra q e z è uguale all’angolo tra w e l’asse
reale, ovvero  -  = -  ovvero  =  -  . Nella terza figura abbiamo che  -  = -  ovvero  =  -  , gli angoli
nel terzo e quarto quadrante sono considerati negativi perché si considerano convessi. Nella quarta figura infatti la
situazione è -  +  =  ovvero  =  -  . (ndmax)
L’unità immaginaria come operatore di rotazione
Particolarmente importante e interessante è il ruolo geometrico che riveste l’unità immaginaria i , la
quale è a sua volta rappresentata da un vettore di modulo unitario, |i| = √12 + 02 = 1 .
Osserviamo cosa accade quando moltiplichiamo un numero complesso qualsiasi per i .
Ad esempio, consideriamo z = 3 + i 2 , applicando la definizione di prodotto e la proprietà
dell’unità immaginaria i 2 = 1 :
(3 + i 2)  i = 3i + i 2 2 = - 2 + 3i .
Notiamo che il modulo resta invariato (parte reale e parte immaginaria si scambiano di ruolo) ma il
vettore z  i risulta ruotato di 90° in senso antiorario rispetto a z .
Cosa succede se dividiamo z per i ?
Otteniamo
3+𝑖2
𝑖
=
(3 + 𝑖 2)  (−𝑖)
𝑖  (−𝑖)
=
−3𝑖− 𝑖 2 2
−𝑖 2
=
−3𝑖 + 2
1
= 2 - 3i .
𝒛
In questo caso il vettore ha ancora lo stesso modulo di z ma è ruotato di 90° in senso orario,
𝒊
ovvero una rotazione di - 90° .
Da ciò possiamo dedurre che dividere per i equivale a moltiplicare per - i :
1
𝑖
=
1  (−𝑖)
𝑖  (−𝑖)
=
−𝑖
−𝑖 2
=
−𝑖
1
=-i.
In conclusione: dal punto di vista geometrico l’unità immaginaria i si comporta a tutti gli effetti
come un operatore di rotazione di 90° : moltiplicare per i ruota il vettore prodotto di 90° in senso
antiorario, moltiplicare per - i ruota il vettore prodotto di 90° in senso orario.
Moltiplicazioni multiple portano a multiple rotazioni: moltiplicando 2 volte per i si ottiene una
rotazione del vettore prodotto di 180° (z  i  i = z  i 2 = z  (-1) = - z , insomma si ottiene il vettore
opposto al vettore dato.
Ancora: z  i  i  i = z  (- i) = (a + i b)  (- i) = - i a + b = b - i a equivale ad una rotazione di - 90°
ovvero di 270° che sono tre rotazioni consecutive di 90° .

Infine: z  i  i  i  i = z  i 2  i 2 = z  (-1)  (-1) = z , ovvero il vettore prodotto coincide con il vettore
dato: la rotazione è nulla, indistinguibile dalla rotazione di 360° e dunque coerente con
l’interpretazione geometrica attribuita alla moltiplicazione per i .
3. Forma trigonometrica e polare dei numeri complessi
Oltre alla forma algebrica a + i b di un numero complesso sono possibili altre due importanti
forme rappresentative dei numeri complessi: la forma trigonometrica e la forma polare.
La forma trigonometrica dei numeri complessi
Dato il numero complesso z = a + i b la grandezza rz = √𝑎2 + 𝑏 2 rappresenta sia il modulo del
numero complesso che il modulo del vettore corrispondente nel piano di Gauss. Il modulo rz
coincide con il raggio della circonferenza su cui muoviamo il punto z . Immaginiamo adesso di
proiettare il vettore z sull’asse reale. Il vettore z forma l’angolo  con l’asse reale, tale angolo è
detto “ argomento “ del numero complesso z , si indica con “ Arg(z) “ e a volte è anche detto
angolo di fase o semplicemente fase.
La proiezione, grazie alle relazioni trigonometriche tra lati e angoli di un triangolo rettangolo, è data
da rz  cos() . Allo stesso modo la proiezione di z sull’asse immaginario è data da rz  sin() .
Evidentemente da rz  cos() = a costituisce la parte reale del numero complesso mentre
rz  sin() = b costituisce la parte immaginaria del numero complesso.
Abbiamo quindi
z = a + i b = rz  cos() + i rz  sin() = rz  cos() + i sin() .
La rappresentazione trigonometrica dei numeri complessi non è univoca a causa della periodicità
delle funzioni seno e coseno, si ha anche:
z = rz  cos( + 2k) + i sin( + 2k) con kZ .
Se si vuole evitare questa ambiguità è possibile considerare -  <    , nel qual caso  prende il
nome di determinazione principale di Arg(z) e talvolta si indica con arg(z) .
Il complesso coniugato di z è 𝒛 = rz  cos() - i sin() .
Possiamo adesso dimostrare quanto visto nel precedente paragrafo relativamente a prodotto e
divisione. La forma trigonometrica per il numero w di modulo w = rw e argomento  è
w = rw  cos() + i sin() .
Prodotto di numeri complessi in forma trigonometrica
Il prodotto z  w si ottiene applicando le definizioni viste precedentemente:
z  w = rz  cos() + i sin()  rw  cos() + i sin() =
= rz  rw  cos() cos() + i cos() sin() + i sin() cos() - sin() sin() =
= rz  rw  cos( + ) + i sin( +  .
Il prodotto di due numeri complessi è rappresentato da un vettore che ha come modulo il prodotto
dei moduli e come argomento la somma degli argomenti dei numeri dati.
Divisione di due numeri complessi in forma trigonometrica
Per eseguire il quoziente
𝒛
𝒘
=
𝑟𝑧 cos() + 𝑖 sin()
𝑟𝑤 cos() + 𝑖 sin()
moltiplichiamo numeratore e denominatore per il complesso coniugato del denominatore a meno
del modulo, ovvero cos() - i sin() . A numeratore si ottiene
rz cos() + i sin()  cos() - i sin() =
= rz cos() cos() - i cos() sin() + i sin() cos() + sin() sin() =
= rz cos( - ) + i sin( - ) .
A denominatore si ottiene
rw cos() + i sin()  cos() - i sin() = rw 𝑐𝑜𝑠 2 () - i 2 𝑠𝑖𝑛2 () =
= rw 𝑐𝑜𝑠 2 () + 𝑠𝑖𝑛2 () = rw .
Abbiamo ottenuto che
𝒛
𝒘
=
𝑟𝑧 cos( − ) + 𝑖 sin( − )
𝑟𝑤
=
𝑟𝑧
𝑟𝑤
cos( - ) + i sin( - ) .
Il quoziente di due numeri complessi è rappresentato da un vettore che ha come modulo il quoziente
dei moduli e come argomento la differenza degli argomenti dei numeri dati.
Forma polare dei numeri complessi
Le considerazioni svolte nel paragrafo precedente ci consentono di individuare un’altra modalità di
rappresentazione dei numeri complessi, la cosiddetta “ forma polare “, in cui vengono messi in
evidenza il modulo e l’argomento secondo la notazione “ modulo  argomento “, dove il simbolo
“  “ sta ad indicare che quella che segue è la misura di un angolo (in gradi o radianti): ad esempio
2,85  43° oppure 7,2  1,2 .
Dalla forma algebrica alla forma polare e viceversa
Se il numero complesso è espresso in forma algebrica, ad esempio z = 4 + i 3 , bisogna calcolare il
modulo , rz = √42 + 32 = 5 , e l’argomento. Per quest’ultima operazione notiamo che la tangente
dell’argomento  è data dal rapporto tra parte immaginaria e parte reale del numero complesso,
3
nel nostro caso tan() = = 0,75 e dunque arctan(0,75) = 36,87° = 0.64 rad .
4
In forma polare avremo: z = 5  36,87° oppure z = 5  0,64 .
Quindi per passare dalla forma algebrica alla forma polare:
𝑏
a + i b  √𝑎2 + 𝑏 2  arctan( ) .
𝑎
𝑏
Riguardo all’argomento  = arctan( ) è opportuna una considerazione.
𝑎
Come si vede in nella seconda figura il codominio della funzione arcotangente è l’intervallo aperto
 
(- , ) .
2 2
La prima figura è la definizione di tangente, si vede che la funzione tangente, di periodo  e definita nell’intervallo
 
(- , ) : presenta stessi valori per angoli nei quadranti I-III e nei quadranti II-IV . (ndmax)
2 2
Non vi è alcun problema nel calcolo dell’angolo se il numero complesso si trova nel primo
(a > 0, b > 0) o nel quarto quadrante (a > 0, b < 0) .
𝑏
Se il vettore si trova nel secondo quadrante (a < 0, b  0) il risultato di arctan( ) sarà un valore
negativo (-2 + i 3 , arctan(
3
−2
𝑎
) = - 56,31°), chiaramente non corretto: in tal caso è necessario
aggiungere  all’angolo trovato.
Analogamente se ci troviamo nel terzo quadrante (a < 0, b < 0) (-2 - i 3 , arctan(
−3
) = 56,31°)
−2
aggiungeremo  se vogliamo l’angolo concavo (angolo positivo, 56.31° + 180° = 236,31°) oppure
toglieremo  se desideriamo la rappresentazione con angolo convesso (angolo negativo,
56,31° - 180° = - 123,69°).
𝑏
Se la parte reale è nulla, non è possibile il calcolo dell’angolo con arctan( ) , ma è chiaro che in
0
questo caso l’argomento sarà  90° , a seconda del segno della parte immaginaria.
Il numero z = 0 rappresenta un unicum in termini di rappresentazione polare, infatti è l’unico valore per cui il modulo è
nullo e l’argomento non è definito. La scelta di dotarlo di questa proprietà è imposta per far si che la corrispondenza
biunivoca modulo-argomento con i punti del piano di Gauss venga rispettata, se così non fosse il numero complesso
z = 0 verrebbe individuato da una infinità di valori dell’argomento. (YouMath)
Riassumendo:
se z = a + i b = rz  cos() + i sin() la sua forma polare è
z = rz   ,
e la forma polare del suo complesso coniugato 𝒛 = a - i b = rz  cos() - i sin() , poiché è anche
𝒛 = rz  cos(-) + i sin(-) è data da
𝒛
= rz  -  ,
dove -  <    è la determinazione principale di Arg(z) .
Spesso, soprattutto nell’uso tecnico, l’argomento è espresso in gradi, allora - 180° <   180° .
Per la trasformazione inversa, da forma polare ad algebrica, si usa la forma trigonometrica:
rz    rz  cos() + i sin() .
Moltiplicazione e divisione in forma polare
Grazie alla forma trigonometrica abbiamo già messo in evidenza che il prodotto di due numeri
complessi è un numero complesso che ha come modulo il prodotto dei moduli e come argomento la
somma degli argomenti. Questo si traduce direttamente nella regola per il prodotto in forma polare:
rz   rw   = rz rw   +  .
Analoghe considerazioni per la divisione:
𝑟𝑧  
𝑟𝑤  
=
𝑟𝑧
𝑟𝑤
- .
Dal punto di vista dei calcoli è conveniente moltiplicare e dividere numeri in forma polare, ma
somma e sottrazione possono essere eseguite solamente in forma algebrica.
4. Elevamento a potenza di numeri complessi.
Dopo aver preso in considerazione le operazioni fondamentali tra numeri complessi ci chiediamo
ovviamente se e in che modo sia applicabile ad essi il concetto di elevamento a potenza.
Potenza con esponente intero di un numero complesso
Elevare un numero reale a alla potenza n significa moltiplicare a per se stesso n volte.
Estendiamo questa definizione ai numeri complessi:
(a + i b)n = (a + i b)  (a + i b)  …  (a + i b)
n volte ,
e supponiamo valide le note proprietà delle potenze
1.
zn  zm = zn+m
2.
zn / zm = zn–m
3.
(z n) m = z n  m
4.
𝒛 𝑛 = √𝒛
5.
z n  w n = (z  w) n
1
𝑛
Tutto ciò diviene particolarmente interessante se il numero complesso è espresso in forma
trigonometrica e applichiamo la proprietà 5 delle potenze:
z n = 𝑟𝑧𝑛  cos() + i sin() n .
Una interessante proprietà del numero cos() + i sin()
Il numero cos() + i sin() che chiamiamo u (u per unità) gode di alcune proprietà interessanti
sulle quali vale la pena di soffermarsi. Intanto rappresenta, al variare di  , qualsiasi numero
complesso di modulo unitario, infatti cos2() + sin2() = 1 . Per tale motivo, se moltiplicato per
un’altro numero, va a modificare solamente l’argomento e quindi agisce come un vero e proprio
operatore di rotazione di  radianti.



1
3
3
3
2
Verifichiamolo con un esempio. Sia  = (= 60°) , quindi cos( ) + i sin( ) = + i
√3
.
2
Moltiplichiamo ora un qualsiasi altro numero complesso w , ad esempio 3 + i 2 , per questo
numero:
1
(3 + i 2)  ( + i
2
√3
)
2
3
= +i
2
3√3
2
3
3 √3 + 2
2
2
+ i + i 2 √3 = - √3 + i
= - 0,232 + i 3,6 ,
in forma polare - 0,232 + i 3,6  3,61  93,69° (attenzione alla parte reale negativa, si
aggiungono 180°). Se calcoliamo la forma polare di w otteniamo 3 + i 2  3,61  33,69° :

osserviamo che 93.69° - 33,69° = 60° (= ) , mentre ovviamente il modulo non è variato.

3


La moltiplicazione per cos( ) + i sin( ) ha provocato la rotazione di
radianti del vettore 3 + i 2
3
3
3
in senso antiorario.


3
3
L’operazione inversa, cioè la divisione per cos( ) + i sin( ) ha invece l’effetto di provocare una
rotazione di

3
radianti in senso orario, come è facile verificare. In questo caso, assunto come di
norma il verso antiorario come positivo per gli angoli, si può dire che la divisione provoca una

rotazione di - radianti.
3
La cosa è del tutto generale: il prodotto di cos() + i sin() (in forma polare , 1  ) per un
qualsiasi vettore, ne provoca la rotazione in senso antiorario di  radianti se  è positivo,
altrimenti in senso orario se  è negativo.
La divisione di un vettore qualsiasi per cos() + i sin() ne provoca la rotazione in senso orario di
 radianti se  è positivo, altrimenti in senso orario se  è negativo. Infatti
1
cos() + 𝑖 sin()
=
1

cos() − 𝑖 sin()
cos() + 𝑖 sin() cos() − 𝑖 sin()
=
cos() − 𝑖 sin()
𝑐𝑜𝑠 2 () + 𝑠𝑖𝑛2 ()
= cos() + i sin() ,
e visto che il coseno è una funzione dispari ed il seno una funzione pari, si può scrivere
1
cos() + 𝑖 sin()
= cos(- ) + i sin(- ) .
Ovvero, dividere un numero complesso per cos( ) + i sin() equivale a moltiplicarlo per
cos(- ) + i sin(- ) , ottenendo quindi una rotazione oraria di un angolo  . (ndmax)
Formula di De Moivre
La formula afferma che, dato un intero n :
cos() + i sin()n = cos(n) + i sin(n) .
Consideriamo il vettore ua = cos() + i sin() e proviamo a calcolarne il quadrato:
cos() + i sin()2 = cos2() + i 2 sin() cos() - sin2() = cos(2) + i sin(2) ,
dove abbiamo utilizzato le formule trigonometriche di duplicazione per seno e coseno. Si nota
subito che l’argomento di cos() + i sin()2 è il doppio di  . Abbiamo dimostrato la formula di
De Moivre almeno per il caso n = 2 . E’ relativamente semplice dimostrarla anche per n = 3, 4, …,
tuttavia non possiamo procedere indefinitamente con queste verifiche, dobbiamo cercare una
dimostrazione generale della formula.
Dimostrazione per induzione
Esiste una tecnica di dimostrazione matematica molto potente: la dimostrazione per induzione.
Si procede così:
a. si dimostra l’affermazione per un caso particolare, ad esempio n = 1 (base dell’induzione);
b. si dimostra che se l’affermazione vale per un generico caso n , allora sarà valida anche per
n + 1 (passo induttivo);
c. si conclude che, potendo essere n qualsiasi, l’affermazione è vera in generale e con ciò essa
risulta dimostrata (conclusione).
Applichiamo la procedura al nostro caso. Dobbiamo dimostrare che
cos() + i sin()n = cos(n) + i sin(n) .
a. BASE
per n = 1 , cos() + i sin()1 = cos(1) + i sin(1) è banalmente vera.
b. Supponiamo ora che cos() + i sin()n = cos(n) + i sin(n) sia vera per un n qualsiasi,
dimostriamo che allora lo è anche per n + 1 , cioè
PASSO INDUTTIVO:
se è vera cos() + i sin()n = cos(n) + i sin(n) allora è vera
cos() + i sin()n+1 = cos(n + 1)  + i sin(n + 1)  .
Per una proprietà delle potenze
cos() + i sin()n+1 = cos() + i sin()n  cos() + i sin() ,
ma per ipotesi cos() + i sin()n = cos(n) + i sin(n) quindi, ponendo per semplicità
n =  abbiamo che
cos() + i sin()n+1 = cos() + i sin()  cos() + i sin() =
= cos() cos() + i cos() sin() + i sin() cos() - sin() sin() =
= cos( + ) + i sin( + ) = cos(n + ) + i sin(n + ) =
= cos(n + 1) + i sin(n + 1) ,
c. Dato che non abbiamo posto nessuna limitazione per n , n può assumere qualsiasi valore e
dunque la formula di De Moivre è dimostrata.
In generale la potenza n-esima, con n intero, di un numero complesso può essere espressa
come:
rz (cos() + i sin())n = 𝑟𝑧𝑛 (cos(n) + i sin(n)) .
Radici di un numero complesso
L’operazione inversa dell’elevamento a potenza è l’estrazione di radice.
Il numero w è la radice n-esima di z se wn = z , con n intero.
Come è noto l’operazione estrazione della radice n-esima equivale all’elevamento a potenza con
esponente
1
𝑛
:
1
1
𝑛
1
1
(𝒘𝑛 )𝑛 = 𝒛 𝑛  𝒘 𝑛 = 𝒛 𝑛  w = 𝒛 𝑛  w = √𝒛 .
Radice quadrata di un numero complesso in forma algebrica
Se w = a + i b e z = u + i v dalle precedenti relazioni abbiamo (a + i b)2 = u + i v cioè
a2 - b2 + i 2ab = u + i v .
Due numeri complessi sono uguali se sono rispettivamente uguali la parte reale e la parte
immaginaria, dunque (abbiamo c + i d , vogliamo la sua radice quadrata a + i b , quindi le incognite sono a, b
- ndmax):
2
2
{𝑎 − 𝑏 = 𝑢 ,
2𝑎𝑏 = 𝑣
a soluzione del sistema è
√𝒛 = a + i b =  √
𝑢 + √𝑢2 + 𝑣 2
2
Soluzione
i√
− 𝑢 + √𝑢2 + 𝑣 2
2
.
E’ interessante calcolare la radice quadrata per alcuni particolari numeri.
Per z = 4 + i 0 , sostituendo nella precedente formula, abbiamo la radice quadrata
8
√𝒛 = a + i b =  (√2 + i √0 =  2 , come ci aspettavamo.
4
4
Proviamo ora con z = 0 + i 4 , otteniamo √𝒛 = a + i b =  (√2 + i √2) =  (√2 + i √2) : fatto
interessante, la radice quadrata del numero immaginario i 4 (argomento 90°) non è data da un
numero immaginario (ad esempio i 2) ma dal numero complesso  (√2 + i √2) .
La forma polare della radice positiva ci indica chiaramente che l’argomento è dimezzato rispetto a
quello del radicando √2 + i √2 ovvero 2  45° .
Esempio di radice cubica (n = 3) di un numero complesso
Supponiamo di voler trovare la radice cubica di 8 . Nel campo reale abbiamo un’unica soluzione:
3
√8 = 2 . Tuttavia ora sappiamo che un numero reale altro non è che un numero complesso con parte
immaginaria nulla: 8 = 8 + i 0 . Cosa succede se estraiamo la radice cubica di questo numero,
3
√8 + 𝑖 0 ? Avremo ancora un’unica soluzione?
Seguendo la linea di ragionamento del paragrafo precedente, se il numero a + i b è la radice cubica
cercata allora (a + i b)3 = u + i v , cioè
a3 - i b3 + i 3a2b - 3ab2 = u + i v  (a3 - 3ab2) + i (3a2b - b3) = u + i v .
Nel nostro caso particolare (a3 - 3ab2) + i (3a2b - b3) = 8 + i 0 , dobbiamo eguagliare parti reali e
parti immaginarie:
3
2
{𝑎 2− 3𝑎𝑏 3 = 8 .
3𝑎 𝑏 − 𝑏 = 0
La seconda equazione, raccolto il fattore comune b e risolta fornisce tre soluzioni (legge
annullamento del prodotto):
3a2b - b3 = 0  b (3a2 - b2) = 0  b = 0  3a2 - b2 = 0  b =  a √3 .
 Per b = 0 la seconda equazione degenera nell’identità 0 = 0 , e ciò vale anche per gli altri
due casi:
3
2
3
𝑎=2
{𝑎 2− 3𝑎𝑏 3 = 8  {𝑎 = 8  {
,
0=0
3𝑎 𝑏 − 𝑏 = 0
0=0
otteniamo la soluzione 2 + i 0 .
 Per b = a √3 :
3
2
3
𝑎 = −1
𝑎 = −1
{𝑎 2− 3𝑎𝑏 3 = 8  {−8𝑎 = 8  {
 {
,
0=0
𝑏 = − √3
3𝑎 𝑏 − 𝑏 = 0
0=0
otteniamo la soluzione - 1 - i √3 .
 Per b = - a √3 :
3
2
3
𝑎 = −1
𝑎 = −1
{𝑎 2− 3𝑎𝑏 3 = 8  {−8𝑎 = 8  {
 {
,
0=0
𝑏 = √3
3𝑎 𝑏 − 𝑏 = 0
0=0
otteniamo la soluzione - 1 + i √3 .
3
La radice √8 + 𝑖 0 ha allora tre soluzioni nel campo complesso: 2 + i 0 , - 1 - i √3 , - 1 + i √3 .
Radici ed equazioni algebriche
Nel campo dei complessi il numero di radici (dall’esempio almeno fino a n = 3) sembra essere
𝑛
uguale all’indice della radice stessa, ovvero data √𝑥 con x complesso e n intero avremo per
n = 2 , 2 radici, per n = 3 , 3 radici.
Se così fosse e se questa congettura fosse vera per ogni n , la situazione sarebbe più soddisfacente
𝑛
rispetto a quanto accade in campo reale, in cui √𝑥 non ha soluzioni se n è pari e x < 0 , oppure
ha 1 soluzione se n è dispari e x < 0 e 2 soluzioni se n è pari e x > 0 .
L’estrazione di radice di ordine n è in qualche modo correlata all’esistenza di soluzioni (che non a
caso chiamiamo radici) di equazioni algebriche di grado n , come
an xn + an-1 xn-1 + an-2 xn-2 + … + a2 x2 + a1 x1 + a0 = 0 ,
dove i coefficienti ai e la variabile x sono, nel caso più generale, numeri complessi.
Ad esempio, √4096 equivale a risolvere l’equazione di secondo grado x2 = 4096 , da cui si
ottengono le due soluzioni reali x1 = - 64 e x2 = 64 .
3
Estrarre la radice cubica di 4096 , √4096 , significa risolvere l’equazione di terzo grado x3 = 4096
la cui unica soluzione reale è x = 16 .
3
Estrarre la radice quarta di 4096 , √4096 , significa risolvere l’equazione di quarto grado
x4 = 4096 : è una biquadratica, effettuiamo la sostituzione t = x2 , otteniamo t2 = 4096 da cui
t =  64  x2 = - 8  x2 = 8 . La prima equazione non ha soluzioni nel campo dei numeri reali,
mentre la seconda equazione ha due soluzioni reali , x1 = - 8 e x2 = 8 .
La chiusura algebrica, ovvero quanti tipi di numeri ci vogliono?
Il fatto che esistano equazioni non risolubili, o operazioni non eseguibili, all’interno di una certa
struttura algebrica (in linguaggio tecnico si dice che la struttura non è algebricamente chiusa)
costituisce una forte motivazione per l’introduzione di nuovi tipi di numeri. Il campo dei reali non è
chiuso per l’estrazione di radice quadrata perché questa operazione non è eseguibile per numeri
reali negativi. Il campo complesso è invece chiuso per questa operazione.
Nuovi tipi di numero sono stati introdotti nel tempo per risolvere problemi di chiusura algebrica.
I numeri interi relativi Z risolvono il problema di sottrazioni tipo 3 - 5 , impossibili all’interno
dell’insieme dei numeri naturali.
I razionali Q permettono la divisione tra interi non divisibili, ad esempio 3 : 5 .
I reali R si affrontano questioni più delicate quali l’esistenza di numeri irrazionali (come √2) e
di numeri trascendenti come e , numero di Nepero, o  , pi-greco (rapporto tra circonferenza e
diametro), funzioni goniometriche, logaritmi naturali, ecc.
Numeri
trascendenti
I numeri complessi C sono la chiusura algebrica dei numeri reali. Un teorema la cui dimostrazione
esula dallo scopo di questa lezione, detto teorema fondamentale dell’algebra, assicura che tutte le
operazioni e tutte le equazioni algebriche sono risolubili in campo complesso e quindi non è e non
sarà più necessario ricorrere a nuovi tipi di numeri.
Radice n-esima di un numero complesso
Cerchiamo ora di dimostrare che è possibile estrarre la radice di indice n intero di un numero
complesso con n qualsiasi e che il numero di queste radici coincide con l’indice n . E’ utile
ricorrere alla rappresentazione trigonometrica dei numeri complessi. Abbiamo in precedenza
dimostrato la validità della formula di De Moivre:
cos() + i sin() n = cos(n) + i sin(n) ,
grazie ad essa è possibile esprimere la potenza n-esima intera di un numero complesso come
z cos() + i sin() n = z n cos(n) + i sin(n) ,
dove z = rz è il modulo del numero complesso ed è sempre positivo.
Immaginiamo ora di calcolare la radice n-esima di w = w cos() + i sin() e che questa radice sia
𝑛
1
z = √𝒘 = 𝒘 𝑛 , allora z n = w e cioè:
z n cos(n) + i sin(n) = w cos() + i sin() .
Perché questa uguaglianza sia verificata è necessario che
𝑧𝑛 = 𝑤
{ cos(𝑛) = cos() .
sin(𝑛) = sin()
Sappiamo che le funzioni trigonometriche seno e coseno sono periodiche con periodo 2 , per cui
dovremo avere n =  + 2k con kZ .
Da questa equazione ricaviamo:
=

𝑛
+
2𝑘
con kZ .
𝑛
Se kZ avremo valori di  che si ripetono, e quindi radici non distinte.
Se, ad esempio, diamo a k il valore n , abbiamo  =
uguale a

𝑛

𝑛
+
2𝑛
𝑛
e quindi  =

𝑛
+ 2 che è ancora
.
Per avere radici distinte il valore massimo di k sarà n - 1 , dato che per k = n avremmo una radice
già trovata con k = 0 .
Se consideriamo i valori negativi, ad esempio k = - 1 , avremo  =

2
𝑛
𝑛
=( -

𝑛−1
𝑛
𝑛
) + 2 = + 2
=

𝑛
+
2(𝑛 − 1)
𝑛

𝑛
-
2
𝑛
, che però è uguale a
, valore che otterremmo quindi anche con k = n - 1 .
Proseguendo si può facilmente verificare che il valore di  per k = - 2 si può ottenere anche per
k = n - 2 . Quindi possiamo limitarci ai valori positivi di k .
Ogni numero complesso possiede allora n radici distinte, così espresse:
1
 + 2𝑘
√𝒘 = 𝑤 𝑛 cos(
𝑛
𝑛
) + i sin(
 + 2𝑘
𝑛
) con k = 0, 1, 2, …, n - 1 .
Le radici dell’unità
L’unità in campo complesso è il numero 1 = 1 + i 0 oppure la coppia (1, 0) .
Se z n = 1 allora z rappresenta le radici n-esime dell’unità.
In questo caso ( = 0) la formula precedente dà
2𝑘
√1 + 𝑖 0 = cos(
𝑛
𝑛
) + i sin(
2𝑘
𝑛
) con k = 0, 1, 2, …, n – 1 .
Nel caso n = 2 abbiamo (come ci aspettavamo):
2 0  
√1 + 𝑖 0 = cos(
2
2
2 1  
√1 + 𝑖 0 = cos(
2
2
) + i sin(
) + i sin(
2 0  
2
2 1  
2
) = cos(0) + i sin(0) = 1 + i 0 ,
) = cos() + i sin() = -1 + i 0 .
Nel caso n = 4 abbiamo
2 0  
√1 + 𝑖 0 = cos(
4
4
2 1  
√1 + 𝑖 0 = cos(
4
√1 + 𝑖 0 = cos(
4
4
2 2  
4
2 3  
√1 + 𝑖 0 = cos(
4
) + i sin(
4
2 0  
) + i sin(
) = cos(0) + i sin(0) = 1 + i 0 ,
4
2 1  
4


2
2
) = cos( ) + i sin( ) = 0 + i 1 ,
2 2  
) + i sin(
) = cos() + i sin() = -1 + i 0 ,
) + i sin(
) = cos( ) + i sin( ) = 0 - i 0 .
4
2 3  
4
3
3
2
2