Equazioni di I° grado
Un’equazione di I° grado è un’equazione che, ridotta a forma normale, è del tipo ax + b = 0 .
b
a
Se il coefficiente a = 0 e b = 0 l’equazione ammette infinite soluzioni
Se il coefficiente a = 0 e b ≠ 0 l’equazione non ammette soluzioni
Se il coefficiente a ≠ 0 l’equazione ammette l’unica soluzione x = −
(equazione determinata)
(equazione indeterminata)
(equazione impossibile)
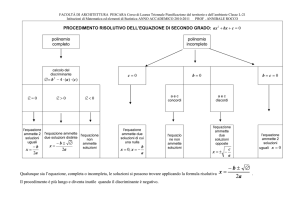
Equazioni di II° grado
Un’equazione di II° grado è un’equazione che, ridotta a forma normale, è del tipo ax 2 + bx + c = 0 .
Per risolverla occorre calcolare il discriminante dell’equazione ∆ = b 2 − 4 ⋅ a ⋅ c .
−b± ∆
Se ∆ > 0 l’equazione ammette due soluzioni reali e distinte x1,2 =
2 ⋅a
−b
Se ∆ = 0 l’equazione ammette due soluzioni reali e coincidenti x1,2 =
2 ⋅a
−b±i −∆
Se ∆ < 0 l’equazione ammette due soluzioni complesse x1,2 =
.
2 ⋅a
Formula Ridotta
Nel caso in cui il coefficiente b dell’equazione è un numero pari si può applicare la formula ridotta:
2
∆ ⎛b⎞
= ⎜ ⎟ −a⋅c
1. Si calcola il discriminante
4 ⎝2⎠
∆
b
− ±
2
4
2. Si applica la formula x1,2 =
a
Caso b = 0 - Equazione Incompleta Pura
2
L’equazione diventa ax + c = 0 .
Se a e c sono discordi, l’equazione ammette due soluzioni reali e opposte x = ± −
Se a e c sono concordi, l’equazione ammette due soluzioni complesse x = ±
c
.
a
c
i.
a
Caso c = 0 - Equazione Incompleta Spuria
L’equazione diventa ax 2 + bx = 0 . Essa ammette sempre una soluzione x = 0 .
Per risolverla occorre raccogliere a fattor comune l’incognita x , ed in seguito applicare la legge dello
x =0
x
0
=
b .
;
annullamento del prodotto:
x ⋅ ( ax + b ) = 0 ;
ax + b = 0
x=−
a
Matematica
www.mimmocorrado.it
1
Esempi di equazioni di I° grado
5
7
2x −7 = 0 ; 2x = 7 ; x = .
1. 3 x + 5 = 0 ; 3 x = −5 ; x = − .
2
3
2. 2 x − 7 = 2 ⋅ ( x − 3 ) ; 2 x − 7 = 2 x − 6 ; 2 x − 2 x = 7 − 6 ; 0 = 1 equazione impossibile.
3. 3 x − 6 = 3 ⋅ ( x − 2 ) ; 3 x − 6 = 3 x − 6 ; 3 x − 3 x = 6 − 6 ; 0 = 0 equazione indeterminata.
Esempi di equazioni di II° grado
x =0
2
1. 5 x − 2 x = 0
x ⋅ (5x − 2 ) = 0 ;
2. 4 x 2 − 3 = 0 ; 4 x 2 = 3 ; x 2 =
5x − 2 = 0 ;
5x = 2 ;
x=
2
5
3
3
3
; x=±
; x=±
4
4
2
2
3. 4 x 2 + 3 = 0 ; 4 x 2 = −3 ; x = −
3 ⋅ −1
3
3
3
i
; x=± −
; x=±
; x=±
4
2
4
4
4. 2 x 2 − 3 x + 1 = 0 ;
∆ = b 2 − 4 ⋅ a ⋅ c = ( −3 )2 − 4 ⋅ 2 ⋅ 1 = 9 − 8 = 1 .
3 −1 2
1
x1 =
= =
4
4
2
3 ±1
− ( −3 ) ± 1
x1,2 =
=
=
2 ⋅2
4
3 +1 4
x2 =
= = 1
4
4
5. 3 x 2 − 5 x + 4 = 0 ;
∆ = b 2 − 4 ⋅ a ⋅ c = ( −5 )2 − 4 ⋅ 3 ⋅ 4 = 25 − 48 = − 23 < 0
x1 =
5 ± 23 i
− ( −5 ) ± − 23
x1,2 =
=
=
6
2 ⋅3
x2 =
6. 4 x 2 − 12 x + 9 = 0 ;
2
7. 3 x − 8 x + 5 = 0 ;
Matematica
5 − 23 i
6
5 + 23 i
6
∆ = b 2 − 4 ⋅ a ⋅ c = ( −12 )2 − 4 ⋅ 4 ⋅ 9 = 144 − 144 = 0 ;
−b
12
3
x1,2 =
=
=
2 ⋅a 2 ⋅4
2
2
2
∆ ⎛b⎞
⎛−8⎞
= ⎜ ⎟ −a⋅c = ⎜
⎟ − 3 ⋅ 5 = 16 − 15 = 1 ;
4 ⎝2⎠
⎝ 2 ⎠
4 −1
=1
x1 =
∆
b
−8
− ±
3
−
± 1
4 ±1
4
2
x1,2 = 2
=
=
=
3
3
a
4 +1 5
=
x2 =
3
3
www.mimmocorrado.it
2