caricato da
common.user2490
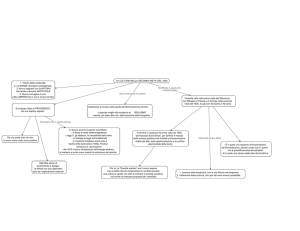
Esercizi di Matematica: Equazioni e Teorema di Pitagora

Nr. 662 X = nr. Di partecipanti quindi la quota procapite è diventa 1800 Se aumentano di 5 persone la quota x 1800 1800 1800 Quindi abbiamo = − 5 che essendo sicuramente x ≠ 0 e x ≠ −5 diventa x +5 x+5 x 1800 x = 1800( x + 5) − 5 x ( x + 5) 5 x 2 + 25 x − 9000 = 0 x 2 + 5 x − 1800 = 0 ∆ = 25 + 7200 = 7225 ≥ 0 − 5 ± 25 + 7200 2 − 5 + 85 80 naturalmente la seconda x1 = = = 40 2 2 − 5 − 85 90 x2 = =− = −45 2 2 x1, 2 = soluzione va scartata Nr. 666 Applicando il Teorema di Pitagora otteniamo (24 − x )2 = x 2 + (x + 3)2 576 + x 2 − 48 x = x 2 + x 2 + 9 + 6 x 576 − 9 − x 2 − 54 x = 0 x 2 + 54 x − 567 = 0 ∆ = 2916 + 2268 = 5184 ≥ 0 − 54 ± 2916 + 2268 2 − 54 ± 5184 x1, 2 = 2 − 54 + 72 18 x1 = = =9 2 2 − 54 − 72 126 x2 = =− = −63 2 2 x1, 2 = Nr.692 D R 3x C Dai teoremi sulle equivalenze sappiamo che 1) Area PRQ = Area ABCD − (Area APRD + Area RCQ + Area PBQ ) Q 2x 4 B A x P Area PRQ = 8*4=32 Area APRD = ( B + b)h (8 − 3x + x )4 = = 2 2 32 − 8 x 2 bh 3 x ( 4 − 2 x ) 12 x − 6 x 2 = = 2 2 2 bh 2 x (8 − x ) 16 x − 2 x 2 Area PBQ = = = 2 2 2 Dobbiamo trovare x in modo che Area PRQ = 10 Allora sostituendo mella 1) otteniamo 32 − 2 x 12 x − 6 x 2 16 x − 2 x 2 10 = 32 − + + 2 2 2 Area RCQ = 8 AB = 8 AP = x AC = 4 QB = 2x RC = 3x 20 = 64 − 32 + 2 x − 12 x + 6 x 2 − 16 x + 2 x 2 2 x 2 − 5x + 3 = 0 ∆ = 25 − 24 = 1 ≥ 0 5 ± 25 − 24 4 5± 1 x1, 2 = 4 5 +1 6 3 x1 = = = 4 4 2 5 −1 4 x2 = = =1 4 4 x1, 2 = Nr. 721 Dobbiamo trovare p in modo tale che PM 2 = 21l 2 Gli unici triangoli rettangoli che possiamo ottenere sono quelli che si ottengono tracciando la proiezione di M su AB e cioè AMH e MHP; nel primo abbiamo che l’angolo in H è 90° l’angolo in A è 60° e l’angolo in M è 30° in questo caso l particolare si ha AH = e 2 3l MH = ora se pongo BP = x 2 e applicando il Teorema di Pitagora al triangolo MHP PM 2 = PH 2 + MH 2 Sostitiuendo e ricordando che l 3 PH = x + 2l − = x + l 2 2 2 3 3 21l = x + l + l 2 2 4 2 Nr. 722 Dobbiamo trovare p in modo tale che PH 2 + PB 2 = 6a 2 Essendo AB = AC per ipotesi abbiamo che ( 2a 2) 2 = AB 2 + AC 2 = 2 AC 2 8a 2 = 2 AC 2 AC = 2a Poniamo AP = x e Consideriamo il triangolo isoscele CHP in 2a − x e considerando il questo caso PH = 2 triangolo PAB si ottiene che PB 2 = x 2 + 4a 2 Sostitiuendo