30.-Geometria euclidea

annuncio pubblicitario

Dispense di Geometria Euclidea
1
Il Teorema di Pitagora
Una volta introdotti i concetti di triangolo e le relative notazioni, uno dei primi problemi che è naturale porsi, e che
ragionevolmente si sono posti tutti geometri - nel senso più letterale del termine - dell’antichità più remota, riguarda
i triangoli rettangoli, ossia i triangoli che presentano un angolo di 90◦ . Ricordiamo che in tali triangoli si dicono
cateti i lati adiacenti all’angolo retto e ipotenusa il lato opposto. Supponiamo che le lunghezze dei cateti di un
triangolo rettangolo siano state assegnate (o esplicitamente calcolate/misurate) e siano pari ad a e b. Nel piano, tutti
i triangoli rettangoli aventi tali quantità come lunghezze dei cateti risulteranno sovrapponibili tra loro attraverso una
traslazione (eventualmente preceduta o seguita da una riflessione), ne consegue che esiste essenzialmente un unico
triangolo rettangolo avente tali caratteristiche. In virtù di ciò, è unica la lunghezza dell’ipotenusa c associata alle
lunghezze dei cateti a e b, ossia:
La lunghezza c dell’ipotenusa è funzione delle lunghezze a, b dei cateti, cioè dipende da a e b attraverso un preciso
meccanismo, che rappresentiamo come c = f (a, b).
Come è facile presumere, la domanda più spontanea a riguardo è quale funzione/meccanismo. Di certo, una funzione
simmetrica di a e di b (ossia tale per cui i ruoli di a e di b possano essere scambiati senza alterare il valore della
funzione in corrispondenza di tali lunghezze), che restituisca metri se supponiamo di prendere il metro come unità
di misura delle lunghezze. Una relazione come c = a3 + b3 non è ragionevole, in quanto c si misura in metri mentre
sia a3 che b3 si misurano in metri cubi. Tuttavia, neppure la relazione c = a + b è ragionevole, in quanto viola la
disuguaglianza triangolare: l’ipotenusa non può essere lunga quanto la somma dei cateti, dev’essere necessariamente
più corta, altrimenti si avrebbe un triangolo con tre vertici allineati (dunque degenere, di certo non rettangolo). Una
relazione che non viola (almeno apparentemente) alcun vincolo di ragionevolezza è invece c2 = a2 + b2 . Di fatto, tale
uguaglianza descrive esattamente quello che accade:
Teorema 1 (Pitagora). Se ABC è un triangolo con un angolo retto in C e indichiamo (come siamo soliti) con le
lettere a, b, c le lunghezze rispettivamente di CB, CA, AB (ossia dei due cateti e infine dell’ipotenusa), si verifica:
p
c 2 = a 2 + b2 ,
che è equivalente a:
c = a2 + b2 .
L’usuale formulazione è “in un triangolo rettangolo, l’area del quadrato costruito sull’ipotenusa è pari alla somma
delle aree dei quadrati costruiti sui cateti ”. Tale risultato è di importanza cruciale per il calcolo della lunghezza di
particolari segmenti, dunque della distanza tra punti, dunque per tutta la geometria euclidea. Prima di passare alla
dimostrazione di tale pietra miliare, introduciamo però una piccola digressione di carattere storico/epistemologico.
L’attribuzione del precedente Teorema alla figura di Pitagora, matematico e filosofo vissuto nella Grecia del
quinto secolo a.C., ha il carattere di un ormai tradizionale falso storico. È accertato infatti che sia i Babilonesi
che gli Egizi, già in epoche molto antecedenti al quinto secolo a.C., fossero a conoscenza del risultato, oltre che
per ovvie esigenze ingegneristiche, anche per il ritrovamento di tavolette recanti calcoli relativi alla misurazione
di terreni agricoli. L’attribuzione a Pitagora è dovuta probabilmente al fatto che egli è stato uno dei primi
uomini, attestati dalla storia, a svincolare lo studio della matematica (a partire dallo studio delle proporzioni, fino
√
alla dimostrazione dell’irrazionalità di 2, dovuta all’allievo Ippaso di Metaponto) dalle questioni prettamente
ingegneristiche, avvicinandola alla concezione metafisica di pensiero allo stato puro.
Passiamo ora alla dimostrazione vera e propria, o meglio, ad una delle numerosissime dimostrazioni possibili. Quella
che riportiamo, ad esempio, è sostanzialmente più semplice di quella riportata da Euclide negli Elementi. Dato il
triangolo ABC, retto in C, ne produciamo tre copie e disponiamo questi quattro triangoli rettangoli come in figura:
Dimostrazione. Vengono a determinarsi due quadrilateri, uno interno ed uno esterno. Questi quadrilateri sono certamente rombi, in quanto hanno quattro lati di uguale lunghezza (quello interno ha lati di lunghezza c, quello esterno di
lunghezza a + b). Il quadrilatero esterno ha inoltre quattro angoli retti, dunque è un rettangolo, ma gli unici quadrilateri che sono simultaneamente sia rombi che rettangoli sono i quadrati. Poiché la somma degli angoli interni di un
triangolo è un angolo piatto, α e β in figura sono angoli complementari. Ne segue che anche gli angoli del quadrilatero
interno sono tutti retti, dunque anche il quadrilatero interno è un quadrato.
Il quadrato esterno è costituito dal quadrato interno e da quattro triangoli uguali a quello di partenza. Segue che se
indichiamo con Q l’area del quadrato più grande, con q l’area del quadrato più piccolo e con T l’area del triangolo
iniziale, si ha:
Q = q + 4 × T.
Chiaramente, Q = (a + b)2 e q = c2 . Per quanto concerne l’area del triangolo rettangolo, se scegliamo un cateto come
base abbiamo che l’altro cateto ne è l’altezza relativa, dunque T = a×b
2 , anche perché il triangolo iniziale è metà di
un rettangolo di dimensioni a e b. La precedente uguaglianza può essere perciò espressa, in maniera perfettamente
equivalente, come:
a×b
(a + b)2 = c2 + 4 ×
.
2
Tuttavia, per effetto della proprietà distributiva e di quella commutativa:
(a + b)2 = (a + b) × (a + b) = a × (a + b) + b × (a + b)
= a×a+a×b+b×a+b×b
= a2 + a × b + a × b + b2
= a2 + 2 × a × b + b2 ,
e poiché 4 ×
a×b
2
= 2 × a × b, la precedente uguaglianza può essere espressa come:
a2 + b2 + 2 × a × b = c2 + 2 × a × b.
Sottraendo ad ambo i membri la stessa quantità, 2 × a × b, otteniamo:
c2 = a2 + b2
che è esattamente quello che volevamo provare.
Una sigla frequentemente usata in queste situazioni è CVD, che sta per come volevasi dimostrare.
Pagina 2 di 55
1
IL TEOREMA DI PITAGORA
Riportiamo anche una dimostrazione grafica del fatto che (a + b)2 = a2 + b2 + 2 × a × b:
L’area del quadrato in figura è pari al quadrato del lato, ossia a
(a + b)2 . D’altro canto tale quadrato può essere decomposto in
due quadrati più piccoli e due rettangoli, aventi le aree riportate.
√
Abbiamo ora un modo di calcolare la lunghezza dell’ipotenusa date le lunghezze dei cateti, attraverso c = a2 + b2 .
Più in generale, date le lunghezze di due lati di un triangolo rettangolo, la lunghezza del lato rimanente può essere
calcolata attraverso una delle seguenti tre formule, tutte equivalenti:
c=
p
a2 + b2 ,
b=
p
c2 − a2 ,
a=
p
c2 − b2 .
Vediamo inoltre, attraverso un esercizio, come il Teorema di Pitagora ci permetta di calcolare la distanza tra due punti
qualunque del piano cartesiano.
Esercizio 2. Nel piano cartesiano sono dati due punti A(2, 4), B(3, 1).
Qual è la loro distanza, ossia la lunghezza del segmento AB?
Tracciando delle parallele agli assi possiamo determinare un punto C come in figura. A questo punto AB
risulta essere l’ipotenusa di un triangolo rettangolo
ABC. Poiché CB = 1 e CA = 3, dal Teorema di
Pitagora segue:
p
√
AB = 12 + 32 = 10.
In generale, la distanza tra un punto A di coordinate A(x1 , y1 ) e un punto B di coordinate B(x2 , y2 ) risulterà pari a:
AB =
p
(x1 − x2 )2 + (y1 − y2 )2 .
Pagina 3 di 55
2
Il Teorema di Pitagora “inverso”
In questa sezione riportiamo un risultato che molto spesso i libri di testo non menzionano,
ma che ha un’importanza pari a quella del suo parente più stretto.
Teorema 3 (Pitagora “inverso”).
Dato un triangolo ABC, denotiamo con a, b, c le lunghezze dei lati opposti ai vertici A, B, C.

2
2
2

 acuto se c < a + b ,
L’angolo in C risulta
retto se c2 = a2 + b2 ,


ottuso se c2 > a2 + b2 .
La dimostrazione è lasciata al lettore.
3
Verso i Teoremi di Euclide ed Erone
Una volta compreso che le lunghezze dei cateti determinano univocamente la lunghezza dell’ipotenusa, e tramite quale
meccanismo, c’è un terzo segmento all’interno di un triangolo rettangolo riguardo il quale vale la pena porsi qualche
interrogativo. Ricordiamo che in un generico triangolo l’altezza relativa ad un lato è quel segmento perpendicolare
al lato scelto che passa per il vertice opposto. Ricordiamo inoltre che il piede dell’altezza è il punto di intersezione
tra l’altezza e il lato scelto (o il suo prolungamento). In un triangolo rettangolo, l’altezza relativa ad un cateto è
semplicemente l’altro cateto. Ma per quanto riguarda l’ipotenusa?
Esercizio 4. Sia ABC un triangolo retto in C con cateti aventi lunghezze a = 4, b = 3.
Qual è la lunghezza dell’altezza relativa all’ipotenusa?
Denotiamo con hC l’altezza relativa all’ipotenusa e con D il piede di tale
altezza. Scelta una base (cioè un lato), l’area di un triangolo è data dal
semiprodotto tra la lunghezza di tale base e la lunghezza dell’altezza
relativa, indipendentemente dalla base scelta. Le nostre premesse
comportano allora:
2 × [ABC] = a × b = c × hC ,
da cui segue:
a×b
.
c
Il Teorema di Pitagora ci garantisce che se i cateti hanno lunghezze 3
√
√
√
e 4, l’ipotenusa ha lunghezza 32 + 42 = 9 + 16 = 25 = 5.
Ma allora:
a×b
4×3
12
hC =
=
=
= 2, 4.
c
5
5
hC =
Notiamo ora che anche il triangolo ACD è retto (in D), e di tale triangolo conosciamo la lunghezza dell’ipotenusa
AC = 3 e quella di un cateto CD = 12
5 . Possiamo allora applicare il Teorema di Pitagora al fine di calcolare la
lunghezza di AD, proiezione di AC su AB:
s
r
r
2 r
p
12
144
225 − 144
81
9
AD = AC 2 − CD2 = 32 −
= 9−
=
=
= .
5
25
25
25
5
Pagina 4 di 55
3
VERSO I TEOREMI DI EUCLIDE ED ERONE
Una volta nota la lunghezza di AD, lo è anche quella di BD, per differenza:
BD = AB − AD = 5 −
9
25 − 9
16
=
=
.
5
5
5
Rimpiazzando 4 e 3 con delle quantità generiche a e b, quindi ripetendo il medesimo ragionamento passo per passo,
abbiamo che:
Teorema 5. In un triangolo ABC, retto in C, l’altezza relativa all’ipotenusa ha lunghezza:
hC =
a×b
a×b
=√
c
a2 + b2
e detto D il piede dell’altezza uscente da C, le proiezioni dei cateti sui lati risultano avere lunghezze pari a:
AD =
b2
,
c
BD =
a2
.
c
L’ultima affermazione riguardo le lunghezze delle proiezioni dei cateti è altresı̀ nota come primo Teorema di Euclide.
L’affermazione nota invece come secondo Teorema di Euclide è conseguenza del Teorema appena dimostrato:
Teorema 6 (Secondo Teorema di Euclide). Se in un triangolo ABC, retto in C, il punto D risulta piede dell’altezza
uscente da C, si verifica:
DA × DB = DC 2 .
e può essere enunciato anche come: “in un triangolo rettangolo, l’altezza relativa all’ipotenusa è media geometrica
delle proiezioni dei cateti sui lati”, in quanto la media geometrica tra due quantità positive u e v è semplicemente
√
definita come la radice quadrata del loro prodotto, u × v.
Questo excursus mostra perciò che entrambi i Teoremi di Euclide possono essere dedotti dal Teorema di Pitagora.
È importante sottolineare che è possibile fare anche il contrario, ossia dimostrare i Teoremi di Euclide da considerazioni
di similitudine di triangoli, per poi dedurne il Teorema di Pitagora. Per questa ragione i Teoremi di Euclide e il
Teorema di Pitagora risultano enunciati equivalenti (diciamo che due affermazioni sono equivalenti se la prima ha
come conseguenza la seconda e viceversa).
Torniamo alla configurazione rappresentata nella pagina
precedente, considerando come noti solo a, b e CD = hC =
a×b
c . Notiamo che i triangoli ACB e ADC sono entrambi
rettangoli e condividono l’angolo in A. Poiché la somma
degli angoli interni di un triangolo è un angolo piatto, due
triangoli aventi due angoli uguali hanno necessariamente
anche il terzo angolo in comune. Segue perciò che ACB
e ADC hanno gli stessi angoli, dunque la stessa “forma”,
dunque i lati in proporzione. Rappresentiamoli uno accanto
all’altro, per chiarezza:
Pagina 5 di 55
2
e consideriamo che poiché hanno i lati in proporzione, si ha z : b = b : c, dunque AD = z = bc .
2
Allo stesso modo, BD = ac , dunque è immediato che si abbia DC 2 = DA × DB. A questo punto, i due Teoremi
di Euclide sono dimostrati senza ricorrere al Teorema Pitagora. D’altro canto è chiaro che valga AB = AD + DB,
dunque:
b2
a2
a2 + b2
c = AB = AD + DB =
+
=
c
c
c
ec=
a2 +b2
c
comporta c2 = a2 + b2 , che è quanto asserito dal Teorema di Pitagora.
Una possibile rappresentazione grafica del fatto che il primo Teorema di Euclide dimostra il Teorema di Pitagora
è la seguente, dove regioni con lo stesso colore risultano equiestese:
Tre esercizi importanti prima di passare alla prossima sezione.
Esercizio 7. (F) Sui cateti e sull’ipotenusa di un triangolo rettangolo vengono costruiti dei triangoli equilateri.
È vero o è falso che l’area del triangolo equilatero più grande è la somma delle aree dei triangoli equilateri più piccoli?
In ogni caso, perché?
Esercizio 8. (F) P è un punto dello spazio cartesiano con coordinate (3, 4, 12). Qual è la sua distanza dall’origine,
ossia dal punto (0, 0, 0)?
Esercizio 9. (FFF) In virtù del Teorema di Pitagora “inverso”, un triangolo che ha lati proporzionali a 3, 4, 5 è
rettangolo, tanto quanto un triangolo che ha lati proporzionali a 5, 12, 13. Chiamiamo terna pitagorica primitiva
un insieme di tre numeri interi e positivi con le seguenti proprietà:
• il quadrato del numero più grande è uguale alla somma dei quadrati degli altri due numeri;
• i due numeri più piccoli non hanno divisori comuni eccetto 1 (ossia sono coprimi).
È vero o è falso che esistono infinite terne pitagoriche primitive? E in ogni caso, perché?
Pagina 6 di 55
4
4
IL TEOREMA DI ERONE
Il Teorema di Erone
Affrontiamo ora un problema sostanzialmente analogo al problema che ha dato inizio a queste dispense. Un triangolo
è univocamente determinato dalle lunghezze di due lati e dall’ampiezza dell’angolo compreso, ma è altrettanto vero
che un triangolo è univocamente determinato dalle lunghezze dei tre lati. Dati tre numeri positivi a, b, c che rispettino
la disuguaglianza triangolare, ossia che verifichino tutte le seguenti condizioni:
a + b > c,
a + c > b,
b + c > a,
a meno di traslazioni (ed eventualmente riflessioni) esiste un unico triangolo ABC avente a, b, c come lunghezze dei
lati. Questo triangolo ha una certa area, [ABC]. Si presenta immediatamente un problema spinoso:
In che modo [ABC] dipende da a, b, c ?
Analogamente alla situazione esaminata nella prima sezione, l’area dovrà essere una funzione simmetrica di a, b, c
(ossia tale da non risentire dell’eventuale scambio di a con b, a con c o b con c) tale da restituire metri quadri se
supponiamo che l’unità di misura delle lunghezze sia il metro. Inoltre, nei casi in cui valga a + b = c, a + c = b o
b + c = a, l’area deve risultare nulla, in quanto area di un triangolo degenere. Non ci sono molte candidate funzioni
che rispettino tutti questi vincoli. Una delle poche è:
f (a, b, c) = K ×
p
(a + b + c) × (a + b − c) × (a + c − b) × (b + c − a),
per una non specificata costante K. D’altro canto, sappiamo già che l’area del triangolo avente lati 3, 4, 5 è 6; se dunque
l’area si comporta secondo le nostre previsioni, la costante K deve valere necessariamente 41 . Ed è effettivamente vero
che:
[ABC]
=
=
1 p
× (a + b + c) × (a + b − c) × (a + c − b) × (b + c − a)
4
p
p × (p − a) × (p − b) × (p − c),
dove abbiamo posto p = a+b+c
(ebbene sı̀, non è troppo conforme al buon senso, ma in genere la lettera p indica il
2
semiperimetro di un triangolo, anziché il perimetro). Tale uguaglianza è conosciuta come Teorema (o formula) di
Erone.
Non ci resta che dimostrarla, ma non è un compito da poco. Fortunatamente abbiamo già acquisito gli strumenti per
farlo, ma anche se il punto di partenza e il punto di arrivo sono chiari, può non essere affatto chiaro quale percorso
intraprendere per riuscire ad andare dal primo al secondo. Adottiamo allora un approccio “zen” e cerchiamo di
effettuare un passo alla volta, limitandoci innanzitutto allo studio di un caso concreto.
Esercizio 10. Un triangolo ha lati di lunghezza 4, 5, 6. Qual è la sua area?
Rammentando che il doppio dell’area è pari al prodotto tra una base e la relativa altezza, ci rendiamo conto che per
rispondere alla domanda posta dall’esercizio è sufficiente capire qual è la lunghezza di un’altezza - una qualsiasi, ad
esempio quella relativa al lato più lungo. A questo punto rappresentiamo la nostra configurazione e, in uno slancio di
genio, battezziamo x, y, z le lunghezze di certi segmenti perché confidiamo che ci condurranno in porto.
Pagina 7 di 55
Notiamo che non conosciamo direttamente i valori di x, y, z. Tuttavia, l’aver tracciato un’altezza ci ha permesso di
dividere il triangolo di partenza in due triangoli rettangoli, e giunti a questo punto dei triangoli rettangoli conosciamo
vita, morte e miracoli. In particolare, il Teorema di Pitagora ci comunica che si ha:
x2 + z 2 = 42 = 16,
y 2 + z 2 = 52 = 25,
e piuttosto banalmente abbiamo x + y = 6. Date queste tre informazioni (riguardo le tre quantità incognite x, y, z),
possiamo ricostruire esplicitamente i valori di x, y e z nel seguente modo. Consideriamo che:
y 2 − x2 = (y 2 + z 2 ) − (x2 + z 2 ) = 25 − 16 = 9.
D’altro canto,
y 2 − x2 = (y − x) × (y + x) = 6 × (y − x),
per cui y − x =
9
6
= 32 . Ci siamo quasi, di x e y ora conosciamo sia la somma che la differenza, e
2 × y = y + y = (y − x) + (y + x) =
ci dice che y =
15
4 .
15
3
+6=
2
2
A questo punto dovremmo intravedere il traguardo. Applicando di nuovo il Teorema di Pitagora,
r
p
z = 52 − y 2 =
225
=
25 −
16
r
400 − 225
=
16
r
175
=
16
r
5 √
7 × 25
= × 7.
16
4
A questo punto, l’aver calcolato z ci permette di concludere:
[ABC] =
1
15 √
×6×z =3×z =
× 7.
2
4
Vittoria, abbiamo risolto un caso particolare, ma la risoluzione di questo caso particolare non ha sfruttato alcuna
peculiarità tipica dei numeri 4, 5, 6. Lo stesso ragionamento può essere ripetuto sostituendo 4, 5, 6 con dei generici
c, b, a e i calcoli, portati in fondo, dimostrano la veridicità del Teorema di Erone.
È importante anche sottolineare certi aspetti concettuali legati all’argomentazione presentata:
• In alcuni problemi geometrici (ma anche in molti problemi aritmetici) risulta particolarmente efficace introdurre
degli elementi ausiliari e lavorare con questi assieme ai dati forniti dal problema medesimo. Purtroppo (o
per fortuna) non c’è alcuna ricetta o oracolo che ci comunichi in anticipo quale sia l’approccio più efficace
(ammettendo che il termine “efficace” possa avere connotazioni oggettive) per la risoluzione di un problema; un
bravo risolutore di problemi ha bisogno sia di esperienza (si può costruire) che di una certa dose di intuizione (si
può costruire anche questa, anche se è un processo più complesso). L’aspetto interessante è che, all’occorrenza,
l’una può rimpiazzare l’altra: cercate perciò di far leva sul vostro punto forte, qualunque esso sia;
Pagina 8 di 55
5
IL BARICENTRO E LA LUNGHEZZA DELLE MEDIANE
• Notate cosa abbiamo fatto: abbiamo introdotto tre quantità, inizialmente incognite, ma legate da tre relazioni.
Queste relazioni ci hanno permesso, attraverso certe manipolazioni, di ricostruire i valori delle quantità introdotte.
Quello che abbiamo fatto è dunque risolvere un sistema di equazioni. Trascurata la natura delle equazioni
e delle manipolazioni coinvolte, ciò è analogo a comprendere quanto vale x sapendo, ad esempio, che si ha
x + y + 2 × z = 10, x + 2 × y + z = 11 e 2 × x + y + z = 13 - vi ricorda niente?
• La stessa tecnica (quella di introdurre non una quantità ausiliaria ma ben tre, legate da certi vincoli) ci permette
anche di calcolare la lunghezza di particolari segmenti all’interno di un triangolo, come ad esempio le mediane.
Studieremo questo problema nel seguito.
5
Il baricentro e la lunghezza delle mediane
Dato un triangolo ABC, denotiamo con MA , MB , MC i punti medi dei lati BC, AC, BC e con mA , mB , mC i segmenti
AMA , BMB , CMC . Diamo a questi ultimi segmenti il nome di mediane. Un primo importante risultato è il seguente:
In un triangolo, le tre mediane risultano sempre concorrenti, ossia passanti per un punto comune.
Chiamiamo questo punto baricentro del triangolo; siamo soliti indicarlo con la lettera G.
Possiamo dimostrare tale risultato immaginando che A, B, C siano punti del piano cartesiano aventi coordinate
A(xA , yA ), B(xB , yB ), C(xC , yC ). In tali ipotesi i punti medi dei lati risultano avere coordinate:
xB + xC yB + yC
xA + xC yA + yC
xA + xB yA + yB
MA
,
,
,
, MB
, MC
2
2
2
2
2
2
e il punto
G
xA + xB + xC yA + yB + yC
,
3
3
risulta appartenere simultaneamente ad AMA , BMB , CMC , in quanto:
3 × G = A + 2 × MA + B + 2 × MB = C + 2 × MC .
Abbiamo dunque che le coordinate del baricentro G sono la media aritmetica delle coordinate dei vertici di ABC.
Abbiamo inoltre che:
Il baricentro G divide ogni mediana in due parti, dove quella che contiene un vertice del triangolo di partenza
ha lunghezza doppia rispetto all’altra.
Abbiamo inoltre che le mediane dividono ABC
in sei triangoli aventi tutti la stessa area.
Pagina 9 di 55
Sorge una nuova questione: come calcolare la lunghezza delle mediane, note le lunghezze a, b, c dei lati BC, AC, AB?
Per venire a capo di tale interrogativo, denotiamo con HA , HB , HC i piedi delle altezze passanti per A, B, C (vedi
x+y
figura), e poniamo x = BHA , y = HA C, z = AHA . Poiché BMA = BC
2 = 2 , si ha:
HA MA2
2
= (BMA − BHA ) =
x+y
−x
2
2
=
1
× (y − x)2 ,
4
e in virtù del Teorema di Pitagora:
2
2
AMA2 = AHA
+ MA HA
= z2 +
1
× (y − x)2 .
4
Considerato però che, sempre in virtù del Teorema di Pitagora,
c2 = x 2 + z 2 ,
b2 = y 2 + z 2 ,
BC 2 = (x + y)2 = x2 + y 2 + 2 × x × y,
non è difficile verificare che si ha:
m2a = AMA2 =
2 × b2 + 2 × b2 − a2
,
4
e analogamente:
m2b = BMB2 =
2 × a2 + 2 × c2 − b2
,
4
m2c = CMC2 =
2 × a2 + 2 × b2 − c2
.
4
Esercizio 11. Un triangolo ABC ha i lati di lunghezze 4, 5, 6. Quali sono le lunghezze delle mediane?
Dimostrazione. Supponendo che a = 4, b = 5, c = 6, per quanto appena provato si ha:
m2a =
106
2 × 52 + 2 × 62 − 42
=
,
4
4
m2b =
2 × 42 + 2 × 62 − 52
79
=
,
4
4
√
Da ciò segue che le lunghezze delle mediane sono
106
2 ,
√
79
2 ,
m2c =
2 × 42 + 2 × 52 − 62
46
=
.
4
4
√
46
2 .
Esercizio 12. Si dimostri che in un triangolo ABC con lati di lunghezze a, b, c e mediane di lunghezze ma , mb , mc
si ha sempre:
a2 + b2 + c2
4
= .
2
2
2
ma + mb + mc
3
Esercizio 13. Dato un triangolo ABC, siano MA , MB , MC i punti medi dei lati BC, AC, AB. Si dimostri che
il baricentro di ABC è anche il baricentro del triangolo mediale di ABC, ossia del triangolo avente vertici in
MA , MB , MC .
Pagina 10 di 55
6
ALTEZZE E ORTOCENTRO
È interessante constatare che:
Le lunghezze delle mediane di un triangolo soddisfano sempre
la disuguaglianza triangolare.
La dimostrazione è interamente racchiusa nella figura a lato: assemblando sei copie del triangolo di partenza si può ottenere un
esagono con lati opposti paralleli. In questo esagono, i segmenti
che congiungono un vertice ad un vertice né adiacente né opposto
hanno lunghezza pari al doppio della lunghezza delle mediane del
triangolo originale.
Esercizio 14. (FFF) Un triangolo ABC ha lati di lunghezze a, b, c e mediane di lunghezze ma , mb , mc .
Un triangolo DEF ha lati di lunghezze ma , mb , mc . Si dimostri che:
[DEF ]
3
= .
[ABC]
4
6
Altezze e ortocentro
Abbiamo visto che le mediane di un triangolo sono sempre concorrenti, ossia passanti per uno stesso punto. La stessa
situazione si verifica per altre triple di rette passanti per i vertici di un triangolo (dette, in generale, ceviane): il
caso che analizziamo in questa sezione è quello delle altezze, ossia delle tre perpendicolari ai lati passanti per i vertici
opposti. Richiamiamo dapprima un po’ di terminologia: dato un triangolo ABC, chiamiamo piede dell’altezza
uscente da A l’unico punto HA sul lato BC (o sul suo prolungamento) tale per cui AHA risulta perpendicolare
a BC, AHA ⊥ BC. Tale punto è anche detto proiezione (ortogonale) di A su BC. Le lunghezze dei segmenti
AHA , BHB , CHC (cioè delle altezze) sono di solito indicate con hA , hB , hC , e per quanto visto sull’area del triangolo
si ha:
2 × [ABC] = a × hA = b × hB = c × hC .
In particolare la lunghezza di un’altezza risulta inversamente proporzionale alla lunghezza del lato relativo.
Ciò comporta che:
• tre quantità positive hA , hB , hC sono effettivamente le altezze di un qualche triangolo se e solo se
rispettano la disuguaglianza triangolare;
1
1
1
hA , hB , hC
• note le lunghezze dei lati, le lunghezze delle altezze possono essere calcolate attraverso la formula di Erone:
hA =
2 × [ABC]
2 p
= × p × (p − a) × (p − b) × (p − c).
a
a
Esercizio 15. (FFF) Si calcoli l’area del triangolo ABC, sapendo che le sue altezze misurano 20, 24 e 30 cm.
Vediamo ora una proprietà (in realtà, una caratterizzazione) delle altezze che permette immediatamente di provare
che queste sono concorrenti.
Pagina 11 di 55
Consideriamo un triangolo ABC e tracciamo le due altezze per B e per C.
Presi due punti P ∈ BHB e Q ∈ CHC , si ha che:
P C 2 − P A2 = a2 − c2 ,
QB 2 − QA2 = a2 − b2 .
Infatti, in virtù del Teorema di Pitagora:
P C 2 − P A2
=
2
2
(P C 2 − P HB
) − (P A2 − P HB
)
=
2
2
CHB
− AHB
=
2
2
2
2
(CHB
+ BHB
) − (AHB
+ BHB
)
=
BC 2 − BA2 = a2 − c2
e possiamo ragionare analogamente per Q. Inoltre i singoli passaggi sono reversibili, ossia:
Un punto P appartiene all’altezza BHB se e solo se P C 2 − P A2 = (a2 − c2 ).
Consideriamo dunque il punto H, intersezione di BHB e CHC . Questo punto verifica sia HC 2 − HA2 = a2 − c2 che
HB 2 − HA2 = a2 − b2 , dunque, per differenza, HC 2 − HB 2 = b2 − c2 . Segue che H appartiene anche ad AHA , dunque
le tre altezze concorrono. Il punto H è detto ortocentro di ABC.
Notiamo che, mentre il baricentro di un triangolo è sempre un punto interno al triangolo, dato che le mediane sono
sempre segmenti interni al triangolo, non è detto che l’ortocentro di un triangolo sia un punto interno; è semplice però
dimostrare che se ABC è acutangolo il suo ortocentro è interno, se ABC è rettangolo il suo ortocentro è il vertice
dell’angolo retto, se ABC è ottusangolo il suo ortocentro è esterno. Vale inoltre che:
Se H è ortocentro di ABC, A è ortocentro di HBC, B è ortocentro di HAC e C è ortocentro di HAB.
Il triangolo HA HB HC è detto triangolo ortico di ABC: torneremo a parlarne più avanti. Nella prossima sezione
introdurremo due punti notevoli che sono i centri di particolari circonferenze, il circocentro e l’incentro.
Pagina 12 di 55
7
7
ASSI, BISETTRICI, CIRCOCENTRO E INCENTRO
Assi, bisettrici, circocentro e incentro
Prima di introdurre i risultati di questa sezione, è importante definire accuratamente cosa intendiamo con il termine
luogo geometrico.
Definizione 16. Diciamo che un certo sottoinsieme E del piano cartesiano è il luogo geometrico dei punti che
verificano una certa proprietà P se si verificano entrambe le seguenti condizioni:
• ogni punto del piano appartenente ad E soddisfa la proprietà P;
• ogni punto del piano che soddisfa la proprietà P appartiene ad E.
Possiamo ad esempio definire la circonferenza in questi termini:
La circonferenza di centro O e raggio r è il luogo geometrico dei punti P tali per cui P O = r.
Rimarchiamo il fatto che un simile enunciato racchiuda in sé due enunciati: il fatto che ogni punto della circonferenza
abbia la stessa distanza da O e il fatto che ogni punto a distanza r da O appartenga alla circonferenza. Oltre alla
circonferenza, due luoghi geometrici di cruciale importanza sono l’asse e la bisettrice. Vediamone le definizioni.
Definizione 17. Dato un segmento AB, la perpendicolare ad AB passante per il suo punto medio è il luogo geometrico
dei punti del piano che verificano P A = P B. Tale retta è detta asse di AB.
Definizione 18. Dato un angolo delimitato da due semirette r ed s, la bisettrice di tale angolo è il luogo dei punti
P interni all’angolo per cui la distanza di P da r eguaglia la distanza di P da s.
Pagina 13 di 55
Esercizio 19. Dati tre punti del piano A, B, C non allineati (ossia non tutti appartenenti ad una stessa retta)
si provi che esiste un’unica circonferenza passante per A, B, C.
Dimostrazione. Chiediamoci dapprima se esiste un qualche punto O per cui si ha OA = OB = OC. Da OA = OB
segue che tale punto deve necessariamente appartenere all’asse di AB, e da OB = OC segue che tale punto deve
appartenere anche all’asse di BC. Dunque O non può essere altro che l’intersezione tra l’asse di AB e l’asse di BC.
Per proprietà transitiva dell’uguaglianza, tale punto realizza anche OA = OC, dunque appartiene anche all’asse di
AC. Abbiamo dunque provato che:
I tre assi di un triangolo (ossia le perpendicolari per i punti medi dei lati) sono sempre concorrenti, e il loro punto di
comune intersezione, detto circocentro, è il centro dell’unica circonferenza passante simultaneamente per tutti e tre
i vertici del triangolo. Quest’ultima è anche detta circonferenza circoscritta al triangolo.
Come nel caso dell’ortocentro, dato un triangolo ABC il suo circocentro non è sempre un punto interno:
lo è se e solo se ABC è acutangolo. Date le lunghezze a, b, c dei lati di un triangolo, il raggio della circonferenza
circoscritta ad ABC è usualmente indicato con la lettera R e talvolta detto circoraggio (calco dall’inglese circumradius).
R può essere calcolato attraverso l’identità:
4 × R × [ABC] = a × b × c,
verificata in virtù del Teorema del seno, che vedremo più avanti.
Pagina 14 di 55
8
8
BISETTRICI E INCENTRO
Bisettrici e incentro
Prima di approcciare il problema di determinare se esista una circonferenza tangente ai tre lati di un triangolo,
è opportuno richiamare il concetto di tangente. Una retta ed una circonferenza, nel piano, possono trovarsi soltanto
in una delle seguenti situazioni:
• La retta e la circonferenza non hanno punti in comune, ossia sono oggetti disgiunti, esterni uno all’altro;
• La retta e la circonferenza hanno due punti di intersezione e si dicono perciò secanti;
• La retta e la circonferenza hanno un unico punto di intersezione: in tal caso si dicono tangenti una all’altra
e il loro punto di intersezione è detto punto di tangenza.
In generale, dato un punto P esterno ad una circonferenza di centro O, esistono due rette passanti per P
che risultano tangenti alla circonferenza:
Denominati T1 e T2 i punti di tangenza, si verifica che:
◦
\
\
OT
1 P = OT2 P = 90
e
OT1 = OT2 ,
in particolare P T2 O e P T1 O, avendo l’ipotenusa P O in comune, risultano due triangoli rettangoli sovrapponibili.
Da ciò segue che:
P T1 = P T2 ,
\
T\
1 P O = T2 P O,
dunque il centro della circonferenza considerata giace sulla retta che divide in due parti uguali l’angolo T\
1 P T2 ,
ossia sulla bisettrice di T\
P
T
.
Ricordiamo
la
definizione
di
bisettrice
come
luogo
geometrico:
1
2
Date due semirette r, s aventi comune origine, la bisettrice dell’angolo delimitato da r ed s è il luogo geometrico
dei punti P del piano aventi la stessa distanza da r e da s.
Pagina 15 di 55
Analogamente al caso del circocentro, tale caratterizzazione ci permette facilmente di dedurre l’esistenza e l’unicità
della circonferenza inscritta di un triangolo, ossia della circonferenza che risulta tangente a tutti e tre i lati del
triangolo assegnato. Il centro di tale circonferenza è detto incentro del triangolo, ed è usualmente indicato con la
lettera I. Il raggio della circonferenza inscritta è detto inraggio ed è usualmente indicato con la lettera r.
Dato un triangolo ABC, supponiamo che una circonferenza di centro P sia tangente sia ad AB che ad AC. Per
quanto visto a inizio sezione, in tali ipotesi P deve appartenere alla bisettrice uscente dal vertice A. Consideriamo
allora il punto di intersezione Q tra la bisettrice uscente da A e la bisettrice uscente da B: per la caratterizzazione
della bisettrice come luogo geometrico, si ha che la distanza di Q da AB uguaglia la distanza di Q da AC, come
d’altronde la distanza di Q da BC uguaglia la distanza di Q da BC. Per transitività dell’uguaglianza, si ha che la
distanza di Q da CA uguaglia la distanza di Q da CB, dunque Q appartiene anche alla bisettrice uscente da C. Ciò
dimostra che:
Le tre bisettrici di un triangolo concorrono in un punto che è il centro dell’unica circonferenza inscritta.
Contrariamente al caso del circocentro (o dell’ortocentro), ma analogamente al caso del baricentro, l’incentro è sempre
un punto interno al triangolo di partenza. È a questo punto interessante considerare le proiezioni IA , IB , IC dell’incentro
I sui lati di un triangolo:
Notiamo che sempre per quanto visto a inizio sezione, AIB = AIC , BIA = BIC e CIA = CIB .
Denotando con ra , rb , rc le lunghezze di AIB , BIC , CIA 1 abbiamo:
ra + rb = c,
ra + rc = b,
rb + rc = a,
e da ciò segue che:
1 Questi
segmenti sono a volta detti segmenti di Soddy, dal nome del chimico (!) inglese Frederick Soddy, 1877-1956,
cui dobbiamo diversi risultati interessanti in geometria euclidea.
Pagina 16 di 55
8
BISETTRICI E INCENTRO
ra =
−a + b + c
= p − a,
2
rb =
a−b+c
= p − b,
2
rc =
a+b−c
= p − c.
2
Notiamo che la formula di Erone assume un aspetto più compatto se espressa in termini di queste quantità:
[ABC]2 = ra × rb × rc × (ra + rb + rc ).
Possiamo inoltre decomporre ABC nei triangoli IAB, IAC, IBC deducendo che:
2 × [ABC] = a × r + b × r + c × r = r × (a + b + c),
da cui [ABC] = p × r. Tale identità può anche essere espressa come:
r
r=
ra × rb × rc
.
ra + rb + rc
Riportiamo ora un risultato importante riguardo le bisettrici.
Teorema 20 (della bisettrice). Se in un triangolo ABC il punto L è piede della bisettrice uscente da A,
\ si ha:
ossia L ∈ BC e AL è bisettrice di BAC,
BL
AB
=
.
CL
AC
Dimostrazione. Indichiamo con LB e LC le proiezioni di L
sui lati AC ed AB, rispettivamente. Indichiamo con HB
e HC i piedi delle altezze uscenti da B e da C. In virtù
del Teorema di Talete si ha:
CL
CB
=
,
LLB
BHB
BL
BC
=
,
LLC
CHC
ma LLB = LLC per definizione di bisettrice come luogo
geometrico. Segue:
BHB
BL
=
=
CL
CHC
Pagina 17 di 55
2∆
AC
2∆
AB
=
AB
.
AC
9
La shoelace formula
Esercizio 21. Un triangolo nel piano cartesiano ha vertici in A(1; 4),B(4; 1) e C(6; 6). Qual è la sua area?
Dimostrazione. Calcolando le lunghezze di CA e CB attraverso
√
il Teorema di Pitagora si ha CA = CB = 34, dunque CAB
è isoscele. Segue che l’altezza relativa ad AB è anche mediana:
detto M il punto medio di AB, le coordinate di M sono date
dalla media aritmetica delle coordinate di A e di B, dunque M
giace in 25 , 52 . Applicando nuovamente il Teorema di Pitagora,
√
√
abbiamo AB = 3 × 2 e CM = 72 × 2, dunque:
[ABC] =
AB × CM
21
=
.
2
2
Nel precedente esercizio, in un certo senso, siamo stati fortunati: calcolando le lunghezze dei lati attraverso il Teorema
di Pitagora ci siamo accorti che il triangolo di partenza era isoscele. Un altro caso “fortunato” sarebbe stato quello in
cui, una volta applicato il Teorema di Pitagora per calcolare le lunghezze dei lati, ci saremmo accorti della rettitudine
di uno degli angoli in A, B o C, in quanto in un triangolo rettangolo l’area è semplicemente data dal semiprodotto
delle lunghezze dei cateti. Ma come procedere nel caso generale? Esiste un modo “semplice” per calcolare l’area di un
triangolo date le coordinate dei suoi vertici? La risposta è affermativa, e risiede nella shoelace formula (“formula
dei lacci di scarpa”, vedremo più avanti che la nomenclatura è eloquente).
Esercizio 22. Un triangolo nel piano cartesiano ha vertici in A(1; 4),B(4; 1) e C(6; 7). Qual è la sua area?
Dimostrazione. Calcolando le lunghezze dei lati di ABC attraverso il Teorema di Pitagora ci accorgiamo che ABC è scaleno, siamo dunque in un caso “sfortunato”. Tuttavia, possiamo
procedere in questo modo: possiamo circoscrivere ad ABC un
rettangolo con vertici nei punti (1; 1), (6; 1), (6; 7), (1; 7), quindi
calcolare l’area di ABC come differenza tra l’area del rettangolo e le aree delle tre “linguette” colorate in figura. Ognuna di
queste “linguette” è un triangolo rettangolo, dunque:
3×3 2×6 5×3
[ABC] = 5 × 6 −
+
+
2
2
2
60 − (9 + 12 + 15)
=
= 12.
2
Notiamo che quest’ultimo approccio non ha sfruttato alcuna peculiarità del triangolo ABC, ed è perciò replicabile nel caso generale in cui i vertici A, B, C abbiano coordinate (a; b), (c; d), (e; f ). Assumendo che A, B, C siano stati
elencati seguendo il verso antiorario e replicando pedissequamente i passi della precedente dimostrazione, abbiamo
che:
Pagina 18 di 55
9
LA SHOELACE FORMULA
Teorema 23 (Shoelace formula). Se i vertici A(a; b), B(c; d), C(e; f ) si susseguono in senso antiorario, vale:
2 × [ABC] = (a × d + c × f + e × b) − (b × c + d × e + f × a).
Vediamo che gli addendi che compaiono all’interno della prima coppia di
parentesi corrispondono ai prodotti dei numeri che figurano agli estremi
di lacci neri (discendenti), mentre gli addendi che compaiono all’interno
della seconda coppia di parentesi corrispondono ai prodotti dei numeri che
figurano come estremi dei lacci rossi (ascendenti).
Nel caso in cui i vertici del triangolo di partenza siano stati elencati in senso orario anziché antiorario, la shoelace
formula ci darà non il doppio dell’area di ABC ma l’opposto. Segue che in ogni caso, il doppio dell’area del triangolo
di vertici A(a; b), B(c; d), C(e; f ) è pari al valore assoluto della differenza tra ad + cf + eb e bc + de + f a.
La shoelace formula ammette una immediata generalizzazione al caso dei poligoni. Supponiamo di avere un poligono
con vertici in A(0; 2), B(3; 0), C(6; 3), D(2; 6): la sua area sarà pari all’area del triangolo ABC sommata all’area del
triangolo ACD.
Applicando separatamente la shoelace formula per il calcolo dell’area di ABC e dell’area di ACD, è facile constatare
che il contributo complessivo dei lacci tra A e C è nullo. Di conseguenza il doppio dell’area di ABCD è pari alla
quantità che si ottiene applicando la shoelace formula ai quattro vertici A, B, C, D. In generale:
Pagina 19 di 55
Teorema 24. Se P1 , P2 , . . . , Pn sono i vertici di un poligono e sono elencati in senso antiorario, il doppio dell’area
del poligono è pari alla quantità che si ottiene applicando la shoelace formula alle coordinate dei vertici P1 , P2 , . . . , Pn .
Nel caso del precedente esercizio abbiamo perciò che l’area di ABCD è data da:
(0 × 0 + 3 × 3 + 6 × 6 + 2 × 2) − (2 × 3 + 0 × 6 + 3 × 2 + 6 × 0)
(9 + 36 + 4) − (6 + 6)
37
=
=
.
2
2
2
È interessante che esista un ulteriore modo per calcolare facilmente l’area di certi poligoni nel piano cartesiano:
Teorema 25 (Pick). Se P1 , P2 , . . . , Pn sono i vertici di un poligono nel piano ed hanno tutti coordinate intere,
l’area del poligono è data da:
P
I + −1
2
dove I è il numero di punti a coordinate intere contenuti strettamente all’interno del poligono e P è il numero di punti
a coordinate intere che giacciono sul perimetro del poligono.
Omettiamo la dimostrazione, ma menzioniamo il fatto che è essenzialmente analoga alla dimostrazione della shoelace
formula nel caso generale.
√ √ √
Esercizio 26. (FFF) Un triangolo ha lati di lunghezze 10, 13, 29. Qual è la sua area? Suggerimento:
è certamente possibile applicare la formula di Erone, ma onde evitare calcoli complicati, è meglio usarne la forma
equivalente, che dipende unicamente da a2 + b2 + c2 e a4 + b4 + c4 . In alternativa, si possono cercare tre punti nel
piano cartesiano che determinano le distanze volute: (0; 1), (3, 0) e (5; 3) sembrano degli ottimi candidati. Cosa ci dice
in tal caso la shoelace formula?
Esercizio 27 (Formula di Brahmagupta). (FFFFF) A partire dalla formula di Erone e dalle proprietà della
circonferenza (si veda più avanti), si dimostri che se a, b, c, d sono le lunghezze dei lati di un quadrilatero ciclico (ossia
inscrittibile in una circonferenza), l’area di quest’ultimo è data dall’espressione
p
1p 2
(p − a)(p − b)(p − c)(p − d) =
(a + b2 + c2 + d2 )2 − 2(a4 + b4 + c4 + d4 ) + 8abcd
4
dove p è il semiperimetro,
a+b+c+d
.
2
Pagina 20 di 55
10
10
LA CIRCONFERENZA E LE SUE PROPRIETÀ NOTEVOLI
La circonferenza e le sue proprietà notevoli
Definizione 28. Dato un punto O nel piano euclideo e una distanza R > 0, chiamiamo circonferenza
(di centro O e raggio R) il luogo dei punti P per cui P O = R.
Definizione 29. Dati due punti distinti A, B appartenenti a una circonferenza, chiamiamo corda il segmento AB e
arco ognuna delle due porzioni in cui A e B suddividono la circonferenza (arco maggiore o minore a seconda che tale
>
arco contenga una semicirconferenza oppure no). Un arco si indica con la notazione AB e, salvo dove diversamente
>
specificato, con l’espressione “l’arco AB” intendiamo l’arco minore tra A e B.
Definizione 30. Chiamiamo diametro di una circonferenza una qualunque corda passante per il centro della circonferenza. La lunghezza di un diametro è il doppio della lunghezza del raggio ed è la massima lunghezza di una
corda.
\e
Definizione 31. Dati tre punti distinti A, B, C appartenenti ad una circonferenza di centro O, diciamo che ABC
[ sono rispettivamente un angolo alla circonferenza e un angolo al centro che insistono sulla corda AC.
AOC
\
Nella medesima situazione, diciamo anche che il punto B vede il segmento AC sotto un angolo pari a ABC.
Teorema 32 (dell’angolo al centro - angolo alla circonferenza).
Se A, B, C sono tre punti distinti appartenenti a una circonferenza di centro O
>
e il punto B appartiene all’arco maggiore AC, si ha:
[ = 2 × ABC.
\
AOC
La tecnica che permette di dimostrare questo Teorema (e molti altri in geometria euclidea) è detta angle chasing,
che in italiano potremmo rendere con caccia all’angolo. Entriamo subito nel dettaglio.
Dimostrazione. I triangoli BOA e BOC sono entrambi isosceli, dun\ = OBA
\ e γ = CBO
\ = OCB.
\ Da ciò segue che gli
que α = BAO
\ e BOC
\ sono l’uno il supplementare di 2 · α e l’altro il
angoli AOB
[ è dato dalla somma tra il
supplementare di 2 · γ. L’angolo AOC
\ e il supplementare di BOC,
\ dunque ha amsupplementare di AOB
piezza pari a 2 · α + 2 · γ, che è esattamente il doppio dell’ampiezza
\ CVD.
dell’angolo ABC,
[ non dipende dalla posizione di B lungo l’arco maggiore >
Notiamo subito che l’angolo AOC
AC, dunque:
>
\ è la stessa.
Per qualunque punto B sull’arco maggiore AC, l’ampiezza dell’angolo ABC
Pagina 21 di 55
>
Ma cosa accade se un certo punto B 0 cade sull’arco minore AC?
>
In tal caso, il punto B 0 appartiene sia all’arco maggiore AB
>
che all’arco maggiore BC. Per il risultato precedente, l’ampiezza di
0 B è la metà dell’ampiezza di AOB
0 C è la
\
\ e l’ampiezza di BB
\
AB
\
metà dell’ampiezza di BOC.
0 C = AB
0 B + BB
0 C è la metà di AOB
\
\
\
\+
Segue che l’angolo AB
◦
\ = 360 − AOC,
[ cioè il supplementare dell’angolo ABC.
\
BOC
Riassumendo:
• Se due punti appartengono ad uno stesso arco di circonferenza,
vedono gli estremi dell’arco sotto lo stesso angolo;
• Se due punti su una circonferenza si trovano da parti opposte
rispetto ad una certa corda, vedono tale corda sotto angoli
supplementari.
In particolare, se 4 punti su una circonferenza sono i vertici di
un quadrilatero convesso, questo ha angoli opposti supplementari.
Viceversa:
• Un quadrilatero convesso può essere inscritto in una circonferenza se e solo se ha angoli opposti supplementari (una coppia
di angoli opposti supplementari è sufficiente, in quanto la somma degli angoli interni di un quadrilatero convesso è un angolo
giro).
Si ha inoltre che il luogo dei punti del piano che vedono un fissato segmento sotto un fissato angolo è dato dall’unione
di due archi di circonferenza, simmetrici rispetto al segmento dato. Si tratta di archi minori se l’angolo assegnato è
ottuso, archi maggiori se l’angolo assegnato è acuto. In particolare, nel caso “intermedio”:
• Il luogo dei punti che vedono un assegnato segmento sotto un angolo retto è la circonferenza
avente tale segmento come diametro;
• Un punto su una circonferenza vede gli estremi di un qualunque diametro sotto un angolo retto.
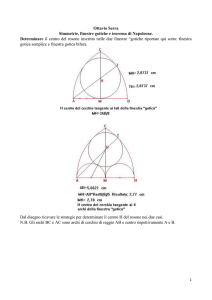
Esercizio 33. Si dimostri che il circocentro di un triangolo rettangolo è il punto medio dell’ipotenusa.
Esercizio 34. Tra tutti i triangoli rettangoli ABC aventi ipotenusa AC = 10 cm, quali sono quelli di area massima?
Pagina 22 di 55
10
LA CIRCONFERENZA E LE SUE PROPRIETÀ NOTEVOLI
Teorema 35 (della corda). Se AC e BD sono due corde di una circonferenza che si intersecano in P , si ha:
P A · P C = P C · P D.
Teorema 36 (della secante-tangente). Se ABCD è un quadrilatero inscritto in una circonferenza, le rette AB e CD
si intersecano in P e una retta per P tange la circonferenza nel punto T , si ha:
P A · P B = P C · P D = P T 2.
È interessante sottolineare che i due Teoremi hanno essenzialmente la stessa dimostrazione, in quanto corrispondono a
configurazioni molto simili, ad eccezione del fatto che il Teorema della corda tratta di rette che si intersecano internamente ad una circonferenza, mentre il Teorema della secante-tangente tratta di rette che si intersecano esternamente.
Entriamo nel dettaglio della dimostrazione del primo enunciato.
\ e P
\
Dimostrazione. Gli angoli CBP
AD sono uguali in quanto insistono sulla corda CD ed hanno vertici sull’arco
>
\
\
maggiore CD. Inoltre gli angoli BP C e DP
A sono uguali in quanto opposti al vertice, dunque supplementari del
medesimo angolo. Ciò comporta che i triangoli P BC e P AD abbiano gli stessi angoli, dunque siano simili. Il Teorema
di Talete garantisce però che triangoli simili abbiano le lunghezze dei lati in proporzione, dunque il rapporto tra P B e
B
PA
P C è uguale al rapporto tra P A e P D. Infine, l’uguaglianza P
P C = P D è equivalente alla tesi, P A·P C = P B ·P D.
Passiamo ora alla dimostrazione del secondo enunciato, trascurando momentaneamente il segmento P T .
\ e DCA
\ sono uguali in quanto insistono sulla corda AD ed hanno vertici sull’arco
Dimostrazione. Gli angoli DBA
>
\
[
maggiore AD. Inoltre gli angoli DP
B e CP
A sono uguali in quanto sono precisamente lo stesso angolo. Ciò comporta
che i triangoli P BD e P CA abbiano gli stessi angoli, dunque siano simili. Il Teorema di Talete garantisce però che
triangoli simili abbiano le lunghezze dei lati in proporzione, dunque il rapporto tra P B e P D è uguale al rapporto tra
B
P C e P A. Infine, l’uguaglianza PP D
= PP C
A è equivalente alla tesi, P A · P B = P C · P D.
Abbiamo dunque che, fissate le posizioni di P e della circonferenza, qualunque retta passante da P che tagli la
circonferenza in due punti E ed F realizza P E · P F = P C · P D = P A · P B (tale prodotto, avente le dimensioni
di un’area, è detto potenza del punto P rispetto alla circonferenza). Ciò resta vero anche nel caso in cui E ed F
siano lo stesso punto (caso limite), cioè nel caso in cui E ≡ F ≡ T , ossia nel caso in cui P T sia una tangente alla
circonferenza. Possiamo inoltre notare che, detto O il centro della circonferenza ed R il suo raggio, il triangolo P T O
Pagina 23 di 55
risulta retto in T . L’applicazione del Teorema di Pitagora ci fornisce allora la seguente versione “estesa”
del Teorema della secante-tangente:
Teorema 37 (della potenza di un punto rispetto ad una circonferenza).
P A · P B = P C · P D = P T 2 = OP 2 − R2 .
Esercizio 38. Nella configurazione rappresentata in figura,
qual è la lunghezza del segmento giallo?
Per il Teorema sulla potenza di un punto rispetto ad una circonferenza:
OP 2 = P A · P B + R2 = 4 · 7 + 9 = 37
dunque la lunghezza di OP è pari a
√
37.
Esistono molti altri risultati importanti riguardo la circonferenza: ne riportiamo ora i principali, senza dimostrazione.
Teorema 39 (Tolomeo). Se A, B, C, D sono i vertici di un quadrilatero convesso nel piano, si ha:
AB · CD + BC · DA ≥ AC · BD
e l’uguaglianza vale se e solo se ABCD è un quadrilatero ciclico, cioè inscrittibile in una circonferenza.
Teorema 40 (Apollonio). Dati nel piano due punti distinti A, B e una fissata quantità k > 0, il luogo dei punti P
A
del piano per cui PP B
= k è una circonferenza avente centro sulla retta AB.
Teorema 41 (Huygens-Steiner). Dati nel piano dei punti A1 , A2 , . . . , An e un ulteriore punto Q,
il luogo dei punti P del piano per cui
P A21 + P A22 + . . . + P A2n = QA21 + QA22 + . . . + QA2n
è una circonferenza passante per Q. La somma in questione, avente le dimensioni di un’area, è detta momento di
inerzia ed è minima in corrispondenza del baricentro di A1 , A2 , . . . , An , ossia in corrispondenza del punto avente
per coordinate la media aritmetica delle coordinate di A1 , A2 , . . . , An .
Pagina 24 di 55
10
LA CIRCONFERENZA E LE SUE PROPRIETÀ NOTEVOLI
Un’altra proprietà molto interessante della circonferenza è quella di essere soluzione di un problema isoperimetrico:
Teorema 42. Tra tutte le curve chiuse e rettificabili di assegnata lunghezza L, la circonferenza è quella che racchiude al
2
2
suo interno l’area maggiore, pari A = L
4π . La disuguaglianza 4πA ≤ L è nota come disuguaglianza isoperimetrica.
Notiamo che un enunciato perfettamente equivalente è tra tutte le porzioni di piano aventi un’area A assegnata,
√
il cerchio è la figura di perimetro minimo, 4πA. Il risultato appena riportato può sembrare piuttosto banale, ma una
sua dimostrazione rigorosa richiede in realtà strumenti di calcolo infinitesimale piuttosto avanzati (come moltiplicatori
di Lagrange o serie di Fourier). Tuttavia, è possibile darne una dimostrazione elementare supponendo che esista
un’unica soluzione al problema, costituita da una curva sufficientemente regolare. Le seguenti osservazioni sono
dovute a Steiner:
• (Mossa (2)) La curva che risolve il problema è di certo frontiera di una regione convessa, altrimenti potremmo
lasciare invariato il perimetro ma incrementare l’area attraverso un processo di simmetrizzazione;
• (Mossa (1)) Il seguente processo non altera né area né perimetro: possiamo staccare dalla nostra curva una
“corda” relativa a un certo arco e re-incollarla alla rovescia. Se la curva da cui siamo partiti è soluzione
del problema isoperimetrico, deve soddisfare il precedente punto anche quando una certa sua corda sia stata
re-incollata alla rovescia;
• Segue che se la curva γ è soluzione, questa deve essere simmetrica rispetto all’asse di una qualunque sua corda.
Segue che l’asse di una qualunque corda passa per un certo punto O, e tutti i punti di γ sono equidistanti da O.
Esempio: un’ellisse (in blu) non è di certo soluzione. Infatti, applicando nell’ordine la mossa (1) e la mossa (2)
possiamo ottenere, a partire dall’ellisse, una regione con
lo stesso perimetro ma che racchiude un’area maggiore.
Ci sono interessanti risultati riguardo piccole varianti del problema appena analizzato:
Teorema 43. Se A1 , A2 , . . . , An , An+1 ≡ A1 sono i vertici di una spezzata chiusa e le lunghezze dei lati
A1 A2 , A2 A3 , . . . , An An+1 sono fissate, l’area racchiusa dalla spezzata è massima quando tutti i suoi vertici giacciono
su una circonferenza.
Teorema 44 (Problema di Didone). Se realizziamo un recinto attraverso un segmento AB e una curva γ che congiunge
A a B di lunghezza assegnata, l’area racchiusa dal recinto è massima quando γ è un arco di circonferenza.
Pagina 25 di 55
Concludiamo questa sezione riportando un risultato assolutamente strabiliante, noto come Teorema di Feuerbach.
Teorema 45 (di Feuerbach). Dato un triangolo ABC, denotiamo con O, G, H circocentro, baricentro e circocentro.
Denotiamo inoltre con MA , MB , MC i punti medi dei lati, con HA , HB , HC i piedi delle altezze, con KA , KB , KC
i punti medi dei segmenti HA, HB, HC. Si verifica che:
• I nove punti MA , MB , MC , HA , HB , HC , KA , KB , KC appartengono tutti ad una stessa circonferenza,
detta circonferenza di Feuerbach o circonferenza dei nove punti di ABC;
• Il centro di tale circonferenza è il punto medio del segmento OH;
• Il raggio di tale circonferenza è la metà del raggio della circonferenza circoscritta;
• Tale circonferenza risulta tangente alla circonferenza inscritta e a tutte le circonferenze ex-inscritte ad ABC.
\ interseca
Esercizio 46. (FFF) Dato un triangolo acutangolo ABC, si dimostri che la bisettrice dell’angolo BAC
>
la circonferenza circoscritta ad ABC nel punto medio dell’arco minore BC.
Esercizio 47. (FFFFF) Dato un triangolo ABC con circocentro O, circoraggio R, ortocentro H
e lati di lunghezze a, b, c, si dimostri che vale:
OH 2 = 9R2 − (a2 + b2 + c2 ).
Pagina 26 di 55
11
11
ISOMETRIE E OMOTETIE
Isometrie e Omotetie
L’impostazione della geometria euclidea basata sui classici postulati (esistenza di punto, retta, piano e relazioni tra
questi, esistenza della circonferenza, esistenza di un’unica parallela/perpendicolare ad una retta data per un punto
esterno) è da sempre molto in voga a livello didattico, ma non è l’unica assiomatizzazione possibile e sperimentata. A
cavallo tra il diciannovesimo e il ventesimo secolo la comunità matematica avvertı̀ la necessità di una nuova sistematizzazione della conoscenza, e, all’interno del programma Erlangen, la figura di Felix Klein si distinse per la proposta
di fondare la geometria euclidea sulle trasformazioni degli oggetti, prima ancora che sugli oggetti stessi. In alcune
scuole francesi, la didattica della geometria è tuttora basata su tale impostazione, anziché su quella che ricalca quasi
fedelmente gli Elementi di Euclide. Di fatto, il germe di questa idea è già contenuto negli Elementi stessi, nel momento in cui l’autore si serve dei concetti di movimento rigido e di sovrapponibilità per dimostrare il primo criterio di
congruenza dei triangoli (riguardo due lati e l’angolo compreso, SAS). In questa sezione cercheremo di effettuare una
panoramica (non esaustiva) di alcune trasformazioni del piano, funzionali all’approccio di Klein, ma la cui conoscenza
è certamente di grande ausilio anche nel caso in cui la didattica della geometria elementare abbia seguito il solco di
Euclide.
Definizione 48. Dati due sottoinsiemi del piano A e B, definiamo la distanza tra questi, in simboli d(A, B), come
il più grande numero reale tale da essere minore o uguale della lunghezza di un qualunque segmento avente un estremo
in A e l’altro in B, in simboli:
d(A, B) =
inf
P Q.
P ∈A,Q∈B
Dalla definizione segue immediatamente che la distanza tra due punti è la lunghezza del segmento che li congiunge e
che la distanza tra due sottoinsiemi non disgiunti è zero. Il successivo caso interessante è quello in cui A sia un unico
punto P e B sia una retta r non passante da P .
In tal caso esiste un’unica perpendicolare ad r passante da P , e il
punto Q di intersezione tra r e la perpendicolare da P è anche detto
proiezione (ortogonale) di P su r. La lunghezza del segmento P Q
è proprio la distanza tra P ed r: infatti, preso un qualunque punto
Q0 ∈ r diverso da Q, il segmento P Q0 risulta essere ipotenusa di un
triangolo retto in Q. In virtù del Teorema di Pitagora, l’ipotenusa di
un triangolo rettangolo è sempre più lunga di un qualunque cateto,
dunque P Q0 > P Q.
Definizione 49. Una trasformazione del piano ϕ è semplicemente un’applicazione/funzione/mappa che associa ad
ogni punto P del piano un unico punto ϕ(P ) detto immagine di P .
Definizione 50. Una trasformazione del piano è detta isometria se conserva le distanze, ossia se, comunque presi
due punti A e B nel piano, la distanza tra l’immagine di A e l’immagine di B è uguale alla distanza tra A e B.
È immediato verificare che le isometrie del piano mandano rette in rette, segmenti in segmenti, punti medi in punti
medi, rette incidenti in rette incidenti, rette parallele in rette parallele. È inoltre semplice provare che le isometrie
sono anche mappe conformi, ossia preservano le ampiezze degli angoli (da intendersi non orientati).
Pagina 27 di 55
Definizione 51. Diciamo che una isometria del piano conserva l’orientazione se l’immagine di un qualunque
triangolo ABC, con i vertici che si susseguono in senso antiorario, è un triangolo con i vertici che si susseguono in
senso antiorario.
Chiamiamo movimento rigido una qualunque isometria che preservi l’orientazione, e punto fisso di una trasformazione qualunque punto che coincida con la sua immagine. Vediamo ora alcuni esempi di isometrie.
TRASLAZIONE. È una trasformazione che dipende da un vettore
e sposta ogni punto del piano nella direzione e nel verso del vettore
dato. Conserva l’orientazione e, tranne nel caso in cui il vettore di
traslazione sia il vettore nullo, non ha punti fissi. Nel piano cartesiano
applicare una traslazione ad un punto è equivalente a sommare alla
sua ascissa e alla sua ordinata due fissate quantità. Un segmento e il
suo traslato risultano sempre paralleli.
RIFLESSIONE o SIMMETRIA ASSIALE. È una trasformazione che dipende da una retta r e porta un punto P nel punto P 0 ,
dall’altra parte rispetto ad r, in modo che P P 0 risulti perpendicolare a r e d(P, r) = d(P 0 , r). È una trasformazione che non conserva
l’orientazione ed ha infiniti punti fissi, tutti i punti di r. Nel piano
cartesiano, riflettere un punto rispetto all’asse delle ascisse/ordinate
corrisponde a cambiare di segno l’ordinata/ascissa del punto. Una
retta non parallela ad r e la sua riflessa si intersecano sempre su r.
ROTAZIONE. È una trasformazione che dipende da un centro O,
un angolo α e un verso (orario o antiorario). Una rotazione porta un
punto P in un punto P 0 tale che OP 0 = OP e P\
OP 0 = α. È una
trasformazione che preserva l’orientazione e, tranne nel caso in cui
l’angolo di rotazione sia nullo, ha un unico punto fisso, il centro O.
Nel piano cartesiano, una rotazione attorno all’origine di 90◦ in senso
antiorario porta un punto di coordinate (x, y) nel punto di coordinate
(−y, x).
Abbiamo dunque che traslazioni e rotazioni sono movimenti rigidi, mentre le simmetrie assiali non lo sono.
È importante sottolineare il fatto che le trasformazioni appena descritte non sono soltanto esempi di isometrie,
ma di fatto esauriscono le isometrie del piano.
Pagina 28 di 55
11
ISOMETRIE E OMOTETIE
Teorema 52. Se due triangoli ABC e A0 B 0 C 0 sono isometrici ed hanno la stessa orientazione (ossia si corrispondono attraverso un movimento rigido), si corrispondono attraverso una traslazione seguita da una rotazione
(equivalentemente, una rotazione seguita da una traslazione).
Teorema 53. Se due triangoli ABC e A0 B 0 C 0 sono isometrici ma non hanno la stessa orientazione, effettuando
una rotazione, una riflessione e una traslazione (o le tre trasformazioni in un qualunque altro ordine prestabilito) è
possibile sovrapporli.
Appropriandoci momentaneamente del linguaggio degli adulti, possiamo riassumere quanto affermato asserendo che
traslazioni, rotazioni e riflessioni generano l’intero gruppo delle isometrie del piano. Sottolineiamo inoltre che i libri
di testo talvolta introducono un quarto tipo di “isometria speciale”, ossia la SIMMETRIA CENTRALE rispetto
a un punto O, che porta un punto P nell’altro punto della retta OP avente la medesima distanza da O.
Questa trasformazione, però, altro non è che un caso speciale di rotazione, di centro O e angolo 180◦ .
Attraverso una simmetria, seguita da una traslazione, seguita da una rotazione, il triangolo ABC
viene sovrapposto al triangolo A000 B 000 C 000 , isometrico ad ABC ma con una diversa orientazione.
Esercizio 54. (FFFF) Presa come unità di misura il centimetro, nel piano cartesiano consideriamo la trasformazione che si ottiene applicando una rotazione di 45◦ in verso antiorario attorno all’origine, seguita da una traslazione
di 2 cm verso destra. Quali e quanti sono i punti fissi di questa isometria? È possibile concludere che tale isometria
è una rotazione? Attorno a quale punto? Di quale angolo, e in che verso?
In realtà, sarebbero bastate le riflessioni a generare l’intero insieme delle isometrie di un piano. Infatti, definita la
composizione tra due trasformazioni f e g come la trasformazione che otteniamo applicando prima g, poi f , in
simboli f ◦ g, abbiamo:
Pagina 29 di 55
11.1
Esistenza e proprietà del baricentro dal punto di vista delle omotetie
Teorema 55. La composizione di due riflessioni rispetto a rette parallele è una traslazione; la composizione di due
riflessioni rispetto a rette incidenti è una rotazione. Viceversa, ogni traslazione si può ottenere componendo due
riflessioni rispetto a due rette parallele e ogni rotazione si può ottenere componendo due riflessioni rispetto a rette
incidenti.
Chiaramente, non possiamo ottenere un movimento rigido componendo un numero dispari di riflessioni, in quanto
ogni riflessione inverte l’orientazione. Facendo riferimento alla precedente figura, avremmo potuto sovrapporre ABC
ad A000 B 000 C 000 attraverso un’unica riflessione, quella determinata dalla retta passante per il punto medio di AA000 e per
il punto medio di CC 000 . Si invita il lettore a provarlo.
11.1
Esistenza e proprietà del baricentro dal punto di vista delle omotetie
Consideriamo un generico triangolo ABC e il suo triangolo mediale A0 B 0 C 0 .
CA
Poiché CBA
0 A = B 0 A = 2, il Teorema di Talete ci garantisce che si abbia
0 0
BC k B C . Analogamente si ha AB k A0 B 0 e AC k A0 C 0 .
Poiché i segmenti BC e B 0 C 0 risultano paralleli e con lunghezze in proporzione 2 : 1, detta G l’intersezione tra BB 0 e CC 0 si ha che una omotetia
di centro G e fattore di dilatazione −2 manda B 0 C 0 in BC. Tale omotetia
manda il punto medio di B 0 C 0 , che denominiamo P , nel punto medio di BC,
0
0 0
0
ossia A0 . Abbiamo dunque che GA
GP = 2, ma d’altra parte A C AB è un
parallelogramma, dunque un quadrilatero con le diagonali che si tagliano
vicendevolmente a metà. Segue che G appartiene anche alla congiungente AA0 e che, inoltre,
AP + P G
A0 P + P G
AG
=
=
= 2.
GA0
GA0
2 · PG
Analogamente si ha
11.2
BG
BG0
=
CG
CG0
= 2.
Il Teorema di Eulero
Teorema 56 (Eulero). In un triangolo ABC qualunque, il circocentro O, il baricentro
G e l’ortocentro H sono allineati. Inoltre G si trova sempre tra O ed H e si ha:
OH = 3 · OG.
Dimostrazione. Con riferimento alla figura nel precedente paragrafo, consideriamo ABC e il suo triangolo mediale
A0 B 0 C 0 . Abbiamo che il baricentro G di ABC coincide con il baricentro di A0 B 0 C 0 , in quanto le mediane di ABC sono
anche mediane di A0 B 0 C 0 . L’omotetia ϕ di centro G e fattore di dilatazione −2 porta A0 B 0 C 0 in ABC, ma poiché
le omotetie sono mappe conformi, ϕ porta l’ortocentro di A0 B 0 C 0 nell’ortocentro di ABC. D’altro canto le altezze
di A0 B 0 C 0 sono gli assi di ABC, dunque l’ortocentro di A0 B 0 C 0 coincide con il circocentro di ABC. Possiamo perciò
concludere che un’omotetia di centro G e fattore di dilatazione −2 porta O in H, da cui segue la tesi.
Esercizio 57. Si dimostri che in un triangolo qualunque i simmetrici dell’ortocentro H rispetto ai lati
appartengono sempre alla circonferenza circoscritta.
Pagina 30 di 55
12
ACCENNI DI GEOMETRIA PROIETTIVA
Vediamo ora anche una dimostrazione del Teorema della bisettrice che fa uso di simmetrie e del Teorema della
secante-tangente.
Nel triangolo ABC, prendiamo L come il piede della
bisettrice uscente da A e definiamo LB ed LC come
le proiezioni di L sui lati AC e AB, rispettivamente.
Costruiamo B 0 come il simmetrico di B rispetto ad
\ B 0 ∈ AC. CoAL: poiché AL è bisettrice di BAC,
struiamo B 00 come il simmetrico di B 0 rispetto a LLB :
poiché LLB ⊥ AC, abbiamo B 00 ∈ AC. Inoltre, da00 C = LBA,
\
[ il punto B 00 appartiene alla
to che LB
circonferenza circoscritta al triangolo LBA. In virtù
del Teorema della secante-tangente CLB 00 e CAB soCA
CL
no triangoli simili, dunque LB
00 = AB . Per simmetria
00
0
LB = LB = LB, da cui:
CL
CA
=
BL
BA
che dimostra nuovamente il Teorema della bisettrice.
12
Accenni di geometria proiettiva
Dato un triangolo ABC e tre rette passanti dai vertici (ceviane) che tagliano i lati BC, AC, BC (o i loro prolungamenti) nei punti PA , PB , PC , è interessante comprendere quale condizione garantisce (o è addirittura equivalente al fatto) che tali ceviane concorrano (ossia passino tutte da uno stesso punto P ), note le lunghezze di
APC , PC B, BPA , PA C, CPB , PB A. Al matematico italiano Giovanni Ceva (1647 - 1734) dobbiamo il seguente risultato
importante:
Teorema 58 (di Ceva). Le ceviane APA , BPB , CPC
di un triangolo ABC concorrono se e soltanto se si ha:
APC · BPA · CPB = APB · BPC · CPA .
Dimostrazione. Dimostriamo per prima l’implicazione apparentemente più semplice: se le ceviane concorrono (assumiamo che concorrano in P ) allora sussiste una certa uguaglianza. Sfruttiamo il seguente fatto: se due triangoli hanno
due basi di pari lunghezza e le altezze relative hanno come rapporto pq , quest’ultimo è anche il rapporto tra le aree.
Partiamo da una solenne ovvietà:
[P AB]
[P AB] [P BC]
=
·
[P AC]
[P BC] [P AC]
e constatiamo che:
[P AB]
[P PA B]
PA B
=
=
.
[P AC]
[P PA C]
PA C
Possiamo procedere in modo analogo per gli altri due rapporti di aree e concludere quanto voluto, ossia che:
PA B PB C PC A
·
·
= 1.
PA C PB A P C B
Pagina 31 di 55
Dimostriamo ora l’altra implicazione, ossia che se vale l’uguaglianza descritta dal Teorema, allora si ha concorrenza.
Ciò è equivalente a dimostrare che se non si ha concorrenza, non si ha uguaglianza (attenzione alla sottigliezza logica,
A implica B è equivalente a la negazione di B implica la negazione di A). Poiché ogni punto QA sulla retta BC è
AB
associato iniettivamente ad un rapporto Q
QA C (ossia a punti diversi corrispondono rapporti diversi), anche tale parte
del Teorema è relativamente banale.
Al Teorema di Ceva fa “da spalla” un altro risultato molto interessante.
Teorema 59 (di Van Obel). Se le ceviane APA , BPB , CPC
di un triangolo ABC concorrono in P , si ha:
AP
APC
APB
=
+
.
P PA
PC B
PB C
Dimostrazione. Una dimostrazione molto breve segue dal medesimo principio applicato nella prima parte
della dimostrazione del Teorema di Ceva:
[ABP C]
[P AB] + [P AC]
PB A
PC A
AP
=
=
=
+
.
P PA
[BP C]
[P BC]
PB C
PC B
È importante anche osservare che se di un punto P interno ad un triangolo ABC conosciamo la collocazione dei
piedi PA , PB , PC delle ceviane per P , conosciamo anche i rapporti tra le distanze di P dai lati di ABC, e viceversa.
La terna costituita delle distanze dai lati fornisce dunque un sistema di riferimento per tutti i punti interni ad un
triangolo. Questo sistema di riferimento è quello delle coordinate trilineari esatte. Notiamo che se dA , dB , dC
sono le distanze di P dai lati BC, AC, AB, si ha:
a · dA + b · dB + c · dC = 2 · [ABC]
indipendentemente dalla collocazione di P . Diciamo perciò che [α; β; γ] sono le coordinate trilineari di P se
le quantità α, β, γ non sono tutte nulle e sono proporzionali alle quantità dA , dB , dC : ad esempio, le coordinate
trilineari dell’incentro sono semplicemente [1; 1; 1], che è come dire [2; 2; 2] o [R; R; R]. In questo strano sistema
di riferimento, che sembra ridondante senza esserlo davvero (le coordinate trilineari sono tre, ma sono definite a
meno di moltiplicazione per una costante non nulla completamente arbitraria) è particolarmente semplice calcolare
l’equazione di una retta passante da due punti, il punto di intersezione di due rette, verificare se tre punti sono
allineati o meno, verificare se tre rette sono concorrenti o meno. Le coordinate trilineari sono un primo esempio
di sistema di riferimento proiettivo.
Questi risultati hanno un’efficacia strategica elevatissima nella discussione di problemi che coinvolgono collinearità (allineamenti), concorrenze e rapporti di aree. Vediamo, ad esempio, cosa ci permettono di scoprire riguardo l’incentro.
Supponiamo che I sia l’incentro del triangolo ABC e che i punti IA , IB , IC siano i piedi delle bisettrici, come riportato
nella figura che segue. Per il Teorema della bisettrice (che a questo punto può essere interpretato come conseguenza
Pagina 32 di 55
12
ACCENNI DI GEOMETRIA PROIETTIVA
diretta del fatto che l’incentro ha coordinate trilineari [1; 1; 1]) abbiamo:
AIB
c
= ,
IB C
a
BIC
a
= ,
IC A
b
CIA
b
= ,
IA B
c
ma dato che AIB + IB C = b, BIC + IC A = c, CIA + IA B = a, le lunghezze dei sei segmenti in questione
sono necessariamente quelle riportate in figura.
Per il Teorema di Van Obel, inoltre:
AI
b+c
=
,
IIA
a
BI
a+c
=
,
IIB
b
CI
a+b
=
,
IIC
c
supponendo dunque di avere a disposizione le lunghezze
delle bisettrici, le distanze dall’incentro dai vertici A, B, C
possono essere ricostruite moltiplicando tali lunghezze per
gli opportuni rapporti
b+c
,
a+b+c
a+c
,
a+b+c
a+b
.
a+b+c
Se i punti A, B, C hanno certe coordinate nel piano cartesiano, si verifica che:
IA =
bB + cC
,
b+c
IB =
aA + cC
,
a+c
IC =
aA + bB
,
a+b
I=
aA + bB + cC
.
a+b+c
Esercizio 60. Nel piano cartesiano sono dati i punti di coordinate A(0; 12), B(−5; 0), C(9; 0).
Quali sono le coordinate dell’incentro I di ABC?
Dimostrazione. Non è particolarmente agevole determinare le equazioni di due bisettrici del triangolo per poi intersecarle. Tuttavia, per il Teorema di Pitagora si ha a = BC = 14, b = AC = 15, c = AB = 13, dunque le coordinate
dell’incentro sono date da:
I=
14 · (0; 12) + 15 · (−5; 0) + 13 · (9; 0)
(0; 168) + (−75; 0) + (117; 0)
=
= (1; 4).
13 + 14 + 15
42
Pagina 33 di 55
13
Inversione circolare
Definizione 61. Date due circonferenze Γ1 , Γ2 che si intersecano in P1 e P2 , il loro asse radicale è dato dalla retta
per P1 e P2 . Nel caso in cui P1 e P2 coincidano (ossia nel caso in cui Γ1 e Γ2 risultino tangenti l’una all’altra) l’asse
radicale è dato dalla retta tangente comune a Γ1 e Γ2 .
Notiamo una proprietà interessante dell’asse radicale, che ci permetterà di estenderne la definizione anche al caso in
cui Γ1 e Γ2 risultino digiunte. Denotiamo come PowΓ (P ) la potenza del punto P rispetto alla circonferenza Γ, ossia
il prodotto P A · P B (da prendersi con segno negativo nel caso in cui P sia interno a Γ) per una qualunque coppia di
punti A, B tali da soddisfare A, B ∈ Γ e P ∈ AB. Per i Teoremi della corda e della secante-tangente, tale prodotto
non dipende dalla retta AB scelta, ma solo dalla collocazione di P rispetto a Γ, e in particolare è uguale ad OP 2 − R2 ,
dove O ed R sono rispettivamente il centro e il raggio di Γ.
Teorema 62. Se Γ1 e Γ2 sono due circonferenze che si intersecano
in A e B, ogni punto P del loro asse radicale soddisfa:
PowΓ1 (P ) = PowΓ2 (P ).
Dimostrazione. Per evidenti ragioni di simmetria, l’asse radicale AB
dev’essere perpendicolare alla congiungente dei centri O1 O2 . Ma allora, per la stessa argomentazione utilizzata per dimostrare il Teorema
di Erone a partire al Teorema di Pitagora (proprietà delle altezze), si
ha:
P O12 − P O22 = AO12 − AO22 = R12 − R22 ,
da cui la tesi segue immediatamente.
Non è difficile realizzare che questa proprietà è verificata da tutti e soli i punti dell’asse radicale.
Possiamo perciò caratterizzare quest’ultimo come luogo geometrico:
Definizione 63. Date due circonferenze Γ1 , Γ2 , il loro asse radicale è il luogo geometrico dei punti P
che hanno la stessa potenza rispetto a Γ1 e a Γ2 .
Notiamo che quest’ultima definizione è coerente con la precedente nel caso in cui Γ1 e Γ2 si intersechino, ma è ben
fondata anche nel caso in cui Γ1 e Γ2 non si intersechino. Vediamo come costruire geometricamente un asse radicale
in quest’ultimo caso.
Denotiamo con O1 ed O2 i centri di Γ1 e Γ2 e consideriamo una
qualunque circonferenza che intersechi Γ1 in A1 , B1 e Γ2 in A2 , B2 .
Denotiamo con P il punto di intersezione di A1 B1 e A2 B2 .
P appartiene di certo all’asse radicale di Γ1 e Γ2 , in quanto:
PowΓ1 (P ) = P B1 · P A1 = P B2 · P A2 = PowΓ2 (P ),
dunque l’asse radicale di Γ1 e Γ2 è la retta passante per P che risulta perpendicolare alla congiungente dei centri O1 O2 . Ogni punto
dell’asse radicale ha una proprietà interessante: è il centro di una circonferenza ortogonale (ossia che interseca perpendicolarmente) sia a
Γ1 che a Γ2 . È sufficiente condurre da tale punto le tangenti a Γ1 e a
Γ2 e considerare le opportune potenze.
Pagina 34 di 55
13
INVERSIONE CIRCOLARE
La caratterizzazione dell’asse radicale come luogo geometrico ha una conseguenza molto interessante:
Teorema 64. Se Γ1 , Γ2 , Γ3 sono tre circonferenze distinte
ed l1 , l2 , l3 sono gli assi radicali delle possibili coppie di
circonferenze, l1 , l2 ed l3 concorrono in un punto che
è detto centro radicale di Γ1 , Γ2 , Γ3 , e che è il centro
dell’unica circonferenza ortogonale sia a Γ1 che a Γ2 che
a Γ3 .
Dimostrazione. Basta ragionare in maniera analoga a
quanto fatto per provare esistenza ed unicità del circocentro o dell’incentro, punti determinati dall’intersezione
di luoghi geometrici. In questo caso, detto P = l1 ∩ l2 , si
ha P ∈ l3 per transitività dell’uguaglianza:
PowΓ1 (P ) = PowΓ2 (P ),
PowΓ2 (P ) = PowΓ3 (P )
comportano PowΓ1 (P ) = PowΓ3 (P ).
Notiamo che l’ultimo risultato fornisce una dimostrazione alternativa dell’esistenza e dell’unicità dell’ortocentro
e dell’incentro di un triangolo ABC. L’ortocentro, infatti, è il centro radicale delle tre circonferenze che hanno
AB, AC e BC come diametri, mentre l’incentro è il centro radicale delle tre circonferenze centrate nei vertici A, B, C
che hanno raggi, rispettivamente, p − a, p − b, p − c.
Esercizio 65 (Cerchio di Taylor). Sia ABC un triangolo
acutangolo e siano HA , HB , HC i piedi delle altezze. Si diB
C
A
C
mostri che i sei punti HA
, HA
, HB
, HB
, HCA , HCB determinati dalle proiezioni di HA , HB , HC sui lati del triangolo appartengono sempre ad una stessa circonferenza (detta
circonferenza di Taylor di ABC).
Segnaliamo che anche il problema #1 delle IMO 2008
riguarda una configurazione simile.
Esercizio 66 (retta di Simson). Sia ABC un triangolo qualunque e P un punto appartenente alla circonferenza
circoscritta ad ABC. Dette PA , PB , PC le proiezioni di P sui lati di ABC (o sui prolungamenti degli stessi),
si dimostri che PA , PB PC sono allineati.
Pagina 35 di 55
Definizione 67. L’inversione circolare rispetto ad un punto O e ad un raggio R (oppure, equivalentemente, rispetto
ad una circonferenza di centro O e raggio R) è quella trasformazione del piano che manda un punto P 6= O nell’unico
punto Q per cui:
• O, P, Q giacciono sulla stessa semiretta avente origine in O;
• vale OP · OQ = R2 .
Questa particolare trasformazione del piano non è né una isometria né una omotetia, ma è una mappa conforme, ed
ha diverse proprietà interessanti, in primis quella mandare rette o circonferenze in rette o circonferenze, conservando
eventuali tangenze. È inoltre una trasformazione involutiva, ossia una trasformazione che applicata due volte
riporta nella configurazione iniziale.
In ognuna delle tre configurazioni riportate, gli oggetti in rosso sono uno l’inverso dell’altro rispetto alla circonferenza
in blu. Quel che accade per effetto del Teorema della secante-tangente è quanto segue:
• invertendo una retta r rispetto a un punto O ∈ r, otteniamo la medesima retta,
sebbene la trasformazione non la fissi punto-per-punto;
• invertendo una retta r rispetto a un punto O 6∈ r, otteniamo una circonferenza;
• invertendo una circonferenza Γ rispetto a un punto O 6∈ Γ, otteniamo una nuova circonferenza;
• invertendo una circonferenza Γ rispetto a un punto O ∈ Γ, otteniamo una retta;
• una circonferenza coincide con la sua inversa se e solo se è ortogonale alla circonferenza di inversione.
Abbiamo inoltre che le distanze tra punti vengono trasformate in modo peculiare.
Supponiamo che A e B siano gli estremi di un segmento e che A−1 e B −1
siano le immagini di A e B secondo una inversione circolare rispetto ad una
circonferenza di centro O e raggio R. Poiché OA · OA−1 = OB · OB −1
abbiamo che ABB −1 A−1 è un quadrilatero ciclico e il triangolo OAB è
simile al triangolo OB −1 A−1 . Di conseguenza:
A−1 B −1 = AB ·
OA−1
OA−1 · OA
R2
= AB ·
= AB ·
.
OB
OA · OB
OA · OB
È importante tuttavia sottolineare che se due circonferenze si corrispondono attraverso una inversione circolare,
i loro centri non sono in generale l’uno l’inverso dell’altro.
Pagina 36 di 55
13
INVERSIONE CIRCOLARE
Già soltanto quanto esposto rende l’inversione circolare uno strumento estremamente potente nella risoluzione di
problemi che coinvolgono una o più circonferenze. Vediamo ad esempio una dimostrazione del Teorema di Tolomeo
che fa uso dell’ultimo risultato, e un esercizio sull’arbelos archimedeo.
Supponiamo che A, B, C, D siano quattro punti su una circonferenza
Γ di centro O, ordinati in senso orario o antiorario. Invertiamo i punti
B, C, D rispetto alla circonferenza di centro A e raggio AO = R,
ottenendo B −1 , C −1 , D−1 . Poiché A ∈ Γ, gli ultimi tre punti sono tra
loro allineati, dunque si verifica B −1 C −1 + C −1 D−1 = B −1 D−1 .
Per trasformazione delle distanze sotto inversione, ciò comporta:
BC
CD
BD
+
=
AB · AC
AC · AD
AB · AD
che è equivalente a:
BC · AD + CD · AB = BD · AC.
Analogamente, è facile dimostrare che se ABCD non è un quadrilatero ciclico, allora BC · AD + CD · AB > BD · AC.
Esercizio 68 (Arbelos archimedeo). Nella configurazione riportata
in figura, qual è il raggio del cerchio marcato con un punto interrogativo?
Dimostrazione. Denominando Γ1 , Γ2 , Γ3 le circonferenze iniziali (aventi raggi rispettivamente 1,2 e 3) e invertendo tutta la costruzione rispetto alla
circonferenza tratteggiata in viola, abbiamo che il problema è analogo a determinare una circonferenza tangente a due rette parallele (Γ−1
e Γ−1
1
2 ) e
ad una terza circonferenza, anch’essa tangente alle ultime due rette (Γ−1
3 ).
Questo problema, tuttavia, è banale, ed è risolto da un opportuno traslato
−1
di Γ−1
. Detto O il centro della circonferenza in viola e Q il
3 , in figura ?
−1
centro di ? , abbiamo che ?−1 ha raggio 32 e OQ2 = 37
4 per il Teorema
−1
di Pitagora. La potenza di O rispetto a ?
è perciò 7, e se A √
e B so−1
e
no due√punti su un diametro di ? allineati con O, si ha OB = 37+3
2
OA = 37−3
.
Invertendo
A
e
B
rispetto
alla
circonferenza
viola,
otteniamo
2
un diametro di ?, che pertanto misura:
2
2
12
√
√
4·
−
=
.
7
37 − 3
37 + 3
Segue che il raggio del cerchio desiderato misura 67 .
Quanto dimostrato ammette una generalizzazione in grande stile, nota come Teorema dei quattro cerchi di Descartes (Cartesio). Tale risultato ha come conseguenza la possibilità di partizionare un cerchio in cerchi con curvature
intere, configurazione già nota ad Apollonio e per questo generalmente indicata con i termini Apollonian gasket.
All’interno del medesimo filone si inseriscono anche due risultati estremamente sorprendenti, noti come Porisma di
Steiner e Porisma di Poncelet.
Pagina 37 di 55
Teorema 69 (Descartes, 1643). Se Γ1 , Γ2 , Γ3 , Γ, 4 sono quattro circonferenze mutuamente tangenti esternamente
(ognuna è tangente alle altri tre) e definiamo la curvatura κi come il reciproco del raggio di Γi , si verifica:
(κ1 + κ2 + κ3 + κ4 )2 = 2 κ21 + κ22 + κ23 + κ24 .
Il Teorema continua ad essere valido nel caso degenere in cui una delle circonferenze Γi sia una retta: in tal caso è
sufficiente prendere κi = 0. Frederick Soddy e Thorold Gosset, anticipati da Lachlan nel 1886, hanno generalizzato
tale risultato anche in dimensione n ≥ 2. Il tal caso il risultato è noto come Teorema di Soddy-Gosset.
Notiamo che dati tre cerchi Γ1 , Γ2 , Γ3 tangenti esternamente uno all’altro, esistono due circonferenze tangenti sia a
Γ1 che a Γ2 che a Γ3 , una esterna e una che contiene al suo interno le tre precedenti, compatibilmente con il fatto che
un’equazione di secondo grado munita di una soluzione ne ha necessariamente anche un’altra. Con riferimento alla
tesi del Teorema di Descartes, fissati i valori di κ1 , κ2 , κ3 , i due valori di κ4 che soddisfano l’equazione, uno negativo
e l’altro positivo, corrispondono ai precedenti due casi. Ad esempio, considerando il caso (κ1 ; κ2 ; κ3 ) = (2; 2; 3), si
ottiene la seguente configurazione:
dalla quale è possibile ripartire: considerando (κ1 ; κ2 ; κ3 ) = (−1; 2; 3) si ottiene una soluzione che già conosciamo,
κ4 = 2, ed una nuova, κ4 = 6. Iterando il processo indefinitamente, si ottiene un Apollonian gasket, una partizione
di un cerchio di raggio unitario in cerchi di curvatura intera:
Una conseguenza interessante del Teorema di Descartes è anche la seguente:
Teorema 70. Se due cerchi Γ1 , Γ2 con curvature κ1 , κ2 sono tra loro tangenti esternamente, e sono inoltre tangenti
√
ad una retta r, le curvature dei due cerchi tangenti a Γ1 , Γ2 , r sono date da κ1 + κ2 ± 2 κ1 κ2 .
Pagina 38 di 55
13
INVERSIONE CIRCOLARE
Definizione 71. Date due circonferenze ΓA , ΓB , l’una interna all’altra, diciamo che le circonferenze Γ1 , Γ2 , . . . , Γn ≡
Γ0 , Γn+1 ≡ Γ1 determinano una catena di Steiner di lunghezza n se per ogni k tra 1 ed n la circonferenza Γk risulta
tangente a Γk−1 , Γk+1 , ΓA e ΓB .
Quella rappresentata in figura, ad esempio, è una catena di Steiner
di lunghezza 6. Fissate le posizioni di ΓA , ΓB , Γk , è chiaro che
sono fissate le posizioni di Γk−1 e Γk+1 . Un risultato piuttosto
sorprendente è il seguente:
Teorema 72 (Porisma di Steiner). Se Γ1 , Γ2 , . . . , Γn è una catena
di Steiner di lunghezza n relativa a ΓA , ΓB , lo resta anche modificando a piacimento la posizione di Γ1 , nel rispetto dei vincoli di
tangenza a ΓA e ΓB , e ricollocando di conseguenza Γ2 , . . . , Γn .
Dimostrazione. Il risultato è banale nel caso in cui ΓA e ΓB siano concentriche. Se ΓA e ΓB non lo sono, esiste
comunque una inversione circolare che le manda in due circonferenze concentriche, preservando le condizioni di tangenza
e mandando Γ1 , . . . , Γn in circonferenze. Tale trasformazione è involutiva, dunque non è restrittivo supporre che ΓA e
ΓB siano concentriche.
Esercizio 73. (FFFFF) ΓA e ΓB sono due circonferenze una interna all’altra, con raggi rA = 4 e rB = 1.
Se ammettono una catena di Steiner di lunghezza 6, qual è la distanza tra i loro centri?
Épater le bourgeois: vale un risultato analogo se rimpiazziamo una catena di Steiner con una spezzata chiusa.
Teorema 74 (Porisma di Poncelet).
Se P1 , P2 , . . . , Pn ≡ P0 , Pn+1 ≡ P1 sono i vertici di un poligono
convesso che risulta simultaneamente inscritto nella circonferenza ΓA e circoscritto alla circonferenza ΓB (bicentrico), modificando la posizione di P1 lungo ΓA e tracciando ripetutamente le
tangenti a ΓB fino a intersecare ΓA si ottiene nuovamente un
poligono bicentrico di n lati.
La tentazione naturale è quella di procedere in analogia con la
precedente dimostrazione, ma c’è un inghippo: applicando una
inversione circolare, non è detto che il lato Pk Pk+1 vada in un
segmento (in generale andrà in arco di circonferenza). Tuttavia...
Dimostrazione. (Sketch) È possibile determinare due trasformazioni, rispettivamente una proiettività ed una affinità, la cui composizione ha la proprietà di preservare le tangenze, mandare segmenti in segmenti e mandare ΓA , ΓB
in due circonferenze concentriche. Provata l’esistenza di tale trasformazione, la tesi è banale.
Pagina 39 di 55
Vediamo ora come coordinare le ultime nozioni apprese per provare
risultati interessanti riguardo una configurazione che coinvolge l’incentro. Dato il triangolo ABC, denotiamo con I il suo incentro e
con IA il suo A-excentro, ossia il punto di intersezione della bisettri\ e delle bisettrici esterne relative a ABC
\
ce interna all’angolo BAC
\ Denotiamo con LA il piede della bisettrice uscente da A.
e BCA.
Per perpendicolarità delle bisettrici interne ed esterne, il quadrilatero BICIA risulta essere un quadrilatero ciclico, inscritto in una
circonferenza (che denotiamo con ΓA ) avente diametro IIA . Denotando con Γ la circonferenza circoscritta ad ABC, vale il seguente
risultato:
Teorema 75 (Lemma della simmediana). Detto N il punto medio
di IIA , centro di ΓA , si ha che N ∈ Γ e che N è punto medio
>
dell’arco BC in Γ.
Dimostrazione. Vale N B = N I = N C = N IA in quanto IBIA e ICIA sono triangoli rettangoli: è perciò sufficiente
provare che N appartiene alla circonferenza circoscritta ad ABC. Ciò è immediato per angle chasing, in quanto
[I + IN
[
\
\ \
BN
C ha ampiezza pari al doppio di BI
A C e da ciò segue che gli angoli BAC e BN C sono supplementari.
Presentiamo subito un ulteriore risultato che avrà ripercussioni profonde nel seguito.
Teorema 76. La potenza di A rispetto a ΓA è esattamente pari al prodotto tra b = AC e c = AB.
Dimostrazione. Sia I che IA , estremi di un diametro di ΓA , appartengono alla bisettrice uscente da A, dunque ΓA
risulta simmetrica rispetto a tale bisettrice. Denotando con C 0 il simmetrico di C rispetto a IIA , abbiamo che:
PowΓA (A) = AI · AIA = AB · AC 0 = AB · AC = bc.
Teorema 77 (Distanze dell’incentro dai vertici e lunghezza delle bisettrici).
2abc
AI = bc − 4rR = bc −
,
a+b+c
2
AL2A
= bc 1 −
a
b+c
2 !
.
Dimostrazione. Possiamo avvalerci di un’osservazione interessante: ABC è il triangolo ortico del triangolo IA IB IC ,
dunque il raggio della circonferenza circoscritta ad IA IB IC è esattamente pari a 2R, con R raggio di Γ. Inoltre IA CB
e IA IC IB sono simili con rapporto di similitudine pari a
IA C
r
=
,
IA IC
AI
dunque AI · IIA = 4rR. Combinando questo risultato con il Teorema (76) otteniamo:
AI 2 = (AI + IIA ) · AI − AI · IIA = bc − 4rR
Pagina 40 di 55
13
INVERSIONE CIRCOLARE
come voluto. Dal Teorema di Van Obel sappiamo che:
AI
b+c
=
,
ILA
a
AI + ILA
ALA
a+b+c
=
=
,
AI
AI
b+c
dunque:
AL2A =
a+b+c
b+c
2
AI 2 =
a+b+c
b+c
2 · bc −
2abc
a+b+c
2
= bc 1 −
a
b+c
2 !
.
Possiamo inoltre notare che “scambiando di ruolo” ABC e IA IB IC il Teorema (75) prova quanto segue:
Teorema 78. Se ABC è un triangolo con ortocentro H, i punti medi dei segmenti HA, HB, HC appartengono alla
circonferenza circoscritta al triangolo ortico.
D’altro canto, la circonferenza circoscritta al triangolo ortico e quella circoscritta al triangolo mediale coincidono.
Teorema 79 (Eulero). Se I ed O sono rispettivamente incentro e circocentro di un triangolo, si ha:
IO2 = R2 − 2Rr.
In particolare, R ≥ 2r, e l’uguaglianza è realizzata solo dai triangoli per cui incentro e circoncentro coincidono,
ossia solo dai triangoli equilateri.
Dimostrazione. Consideriamo un sistema fisico S formato da tre punti materiali in A, B, C, aventi masse a, b, c.
Il centro di massa di tale sistema giace in I, in quanto
I=
aA + bB + cC
.
a+b+c
Consideriamo dunque un punto materiale di massa unitaria collocato in O e determiniamo il suo momento di
inerzia rispetto a S. Da un lato, tale quantità è pari a (a + b + c)R2 . D’altra parte, il Teorema di Huygens-Steiner
prova che:
R2 (a + b + c) = (a + b + c)IO2 + a · IA2 + b · IB 2 + c · IC 2 ,
dove le quantità IA2 , IB 2 e IC 2 sono appena state calcolate. In particolare:
IO2 = R2 −
3abc
+ 4rR = R2 − 2Rr
a+b+c
come voluto.
Teorema 80 (Eulero). Se P è un punto interno ad un triangolo ABC e PA , PB , PC sono le proiezioni di P sui
lati BC, AC, AB, il triangolo PA PB PC è detto triangolo pedale di P e la sua area dipende unicamente dalla
distanza di P dal circocentro O di ABC.
Pagina 41 di 55
Dimostrazione. Per il Teorema di Pitagora generalizzato e il Teorema dell’angolo al centro, le distanze del
circocentro O dai lati di ABC sono date dalle seguenti quantità:
R·
bc + c2 − a2
,
2bc
R·
ac + c2 − b2
,
2ac
R·
ac + b2 − c2
,
2ab
la somma di tali distanze è pari a:
R+
(−a + b + c)(a − b + c)(a + b − c)
=R+r
2abc
(ciò è anche noto come Teorema di Carnot) e le coordinate baricentriche del circocentro sono date da:
O=
1
a2 (b2 + c2 − a2 )A + b2 (a2 + c2 − b2 )B + c2 (a2 + b2 − c2 )C .
(a + b + c)(−a + b + c)(a − b + c)(a + b − c)
Quest’ultima identità permette di determinare rapidamente le coordinate del circocentro di un triangolo date
le coordinate dei vertici, anche nel caso in cui i vertici del triangolo appartengano a Rn con n > 2: le quantità
a2 , b2 , c2 sono infatti immediate da calcolare attraverso il Teorema di Pitagora, indipendentemente dalla dimensione
dello spazio ambiente. L’ultima identità ci permette inoltre di affermare che il circocentro O è il centro di
massa di un sistema S dato da tre punti materiali A, B, C aventi masse a2 (b2 + c2 − a2 ), b2 (a2 + c2 − b2 ) e
c2 (a2 + b2 − c2 ). La strategia per provare il Teorema di Eulero è ora la seguente: supporre che il punto P abbia
coordinate baricentriche P = αA + βB + γC e calcolare il suo momento di inerzia rispetto ad S utilizzando
dapprima il Teorema di Huygens-Steiner: ciò fornisce una espressione che dipende unicamente da OP 2 e da
a, b, c, R2 . Resta da verificare che il momento di inerzia di P rispetto ad S, calcolato attraverso la definizione
del momento di inerzia, è direttamente dipendente dall’area di PA PB PC : in tale contesto è utile ricordare che
P A2 − P B 2 = PC A2 − PC B 2 = (PC A − PC B)c. La conclusione dell’excursus è che vale:
1
OP 2
[PA PB PC ] =
1−
[ABC].
4
R2
Possiamo utilizzare il Teorema del triangolo pedale per fornire una dimostrazione alternativa dell’identità
IO2 = R2 − 2Rr. Dette IA , IB , IC le proiezioni dell’incentro sui lati di ABC, si ha:
(a + c − b)2
(a + b − c)2
(b + c − a)2
−
−
[IA IB IC ] = [ABC] 1 −
,
4bc
4ac
4ab
dunque:
(b + c − a)2
(a + c − b)2
(a + b − c)2
IO2
=
1
−
4
1
−
−
−
R2
4bc
4ac
4ab
e attraverso elementari manipolazioni algebriche:
IO2
(−a + b + c)(a − b + c)(a + b − c)
2r
=1−
=1− .
R2
abc
R
Teorema 81 (Distanza incentro-baricentro).
IG2 =
2(a + b + c)3 − 5(a3 + b3 + c3 ) − 39abc
.
27(a + b + c)
Dimostrazione. Consideriamo un sistema fisico S formato da tre punti materiali A, B, C aventi masse a, b, c. Il
centro di massa di S è dato dll’incentro di I, e il momento di inerzia di S attorno ad I è dato da:
MI = aAI 2 + bBI 2 + cCI 2 = 3abc − (a + b + c)4rR = abc.
Pagina 42 di 55
13
INVERSIONE CIRCOLARE
Calcoliamo il momento di inerzia di S attorno a G:
MG = aGA2 + bGB 2 + cGC 2 =
1X
a(2b2 + 2c2 − a2 ).
9 cyc
G −MI
, da cui segue la tesi.
In virtù del Teorema di Huygens-Steiner, IG2 = Ma+b+c
È interessante constatare che prendendo invece masse unitarie in A, B, C si ha, equivalentemente:
P
P
2
2
ab + ac + bc
2abc
a2 + b2 + c2
cyc AI −
cyc AG
2
GI =
=
−
−
.
3
3
a+b+c
9
Esercizio 82. Dato un triangolo ABC, definiamo Γr come la circonferenza inscritta in ABC e ΓX , per X ∈ {A, B, C},
come la circonferenza tangente a Γr e ai lati di ABC passanti per X. Si determinino i raggi di ΓA , ΓB , ΓC in termini
di a, b, c, r, R.
Suggerimento: Γr e ΓA si corrispondono attraverso una inversione circolare di centro A e raggio AI − r.
Gli estremi di un diametro di ΓA sono dati dalle immagini di IA ∩ Γr secondo tale inversione circolare.
Esercizio 83. Si calcoli la distanza tra circocentro e ortocentro in termini di a, b, c, R.
Dimostrazione. In virtù del Teorema di Eulero sull’allineamento di O, G, H, in un sistema di riferimento centrato nel
circocentro si ha H = A + B + C. Vale però la seguente identità vettoriale:
kA + B + Ck2 = 3(kAk2 + kBk2 + kCk2 ) − kA − Bk2 + kA − Ck2 + kB − Ck2
che comporta:
OH 2 = 9R2 − (a2 + b2 + c2 ).
Tale identità può essere dimostrata anche attraverso il Teorema di Eulero sul triangolo pedale, una volta calcolata
l’area del triangolo ortico.
Esercizio 84. Il punto di Nagel Na di un triangolo ABC è definito nel seguente modo: siano JA , JB , JC i punti di
tangenza delle circonferenze ex-inscritte che giacciono sul perimetro di ABC. Le rette AJA , BJB , CJC concorrono in
un punto per il Teorema di Ceva. Si calcoli, in termini di a, b, c, R, la distanza tra baricentro e punto di Nagel.
Dimostrazione. In virtù della definizione le coordinate trilineari del punto di Nagel sono date da b+c−a
, a+c−b
, a+b−c
,
a
b
c
dunque, in coordinate baricentriche:
Na =
(b + c − a)A + (a + c − b)B + (a + b − c)C
.
a+b+c
Abbiamo perciò:
2
kNa − Gk = R
2
X b + c − a
cyc
1
−
a+b+c 3
2
+2
X b + c − a
cyc
1
−
a+b+c 3
a+c−b 1
−
a+b+c 3
Esercizio 85. Tramite i Teoremi di Eulero o altre considerazioni, si provi che:
Na O =
4∆
· OI 2 = R − 2r.
abc
Pagina 43 di 55
c2
2
R −
.
2
14
Convessità e inviluppo convesso
Una delle principali difficoltà che sorge nella transizione tra geometria del piano e dello spazio è quella di dover
riadattare alcune definizioni e alcuni concetti a un nuovo contesto. Per ovviare a tale difficoltà, una scelta ragionevole
è quella di introdurre un concetto molto generale che prescinde dal numero di dimensioni: tale concetto è quello di
convessità.
Definizione 86. Diciamo che un sottoinsieme E del piano, dello spazio o di un qualunque spazio vettoriale su R,
è convesso se per qualunque coppia di punti P, Q ∈ E, il segmento che congiunge P a Q è interamente contenuto in
E.
Con tale definizione abbiamo ad esempio che ellissi, cerchi o quadrati sono sottoinsiemi convessi del piano, mentre
figure che hanno l’aspetto di stelle, ciambelle o ferri di cavallo non lo sono. Una nozione interessante in sé e di grande
utilità pratica è inoltre quella di inviluppo (o “involucro”, in inglese hull ) convesso di punti.
Definizione 87. Dati due punti P e Q, definiamo l’inviluppo convesso di P e Q come:
Conv (P, Q) = {λ · P + (1 − λ) · Q tali che 0 ≤ λ ≤ 1} .
L’involucro convesso di due punti corrisponde di fatto al segmento che li congiunge. Possiamo notare che prendendo
λ = 0 nella definizione otteniamo il punto Q, prendendo λ = 1 otteniamo il punto P e prendendo λ = 21 otteniamo il
punto medio tra P e Q. Tale nozione si generalizza anche a più punti:
Definizione 88. Dati tre punti A, B, C definiamo il loro inviluppo convesso come:
Conv (A, B, C) = {α · A + β · B + γ · C tali che α, β, γ ≥ 0, α + β + γ = 1} .
L’inviluppo convesso di tre punti è dunque dato dalle combinazioni lineari di tali punti che soddisfano la condizione
d’avere coefficienti non negativi e con somma uguale ad uno. Tali combinazioni lineari si chiamano anche combinazioni convesse: nel caso generale possiamo tranquillamente affermare che l’involucro convesso è l’insieme delle
combinazioni convesse. Riguardo la precedente definizione, è semplice verificare che limitandosi ai casi α = 0, β = 0
e γ = 0 si ritrovano i segmenti BC, AC e AB. L’involucro convesso di tre punti risulta di fatto essere il triangolo
(eventualmente degenere) che ha tali punti come vertici; il caso α = β = γ = 31 dà luogo al baricentro del triangolo,
come già visto.
È importante sottolineare che l’involucro convesso può essere definito, equivalentemente, come il più piccolo (rispetto
alla relazione di contenimento) insieme convesso che contiene i punti assegnati.
A questo punto, possiamo chiamare poligono convesso l’involucro convesso di 3 o più punti non allineati nel piano,
poliedro convesso l’involucro convesso di 4 o più punti non complanari (ossia non appartenenti ad uno stesso
piano) nello spazio tridimensionale, politopo convesso l’involucro convesso di 5 o più punti in uno spazio a quattro
dimensioni2 che non appartengano ad uno stesso sottospazio tridimensionale. Fatto ciò, possiamo definire i poligoni
(tout court) come le unioni connesse di poligoni convessi, i poliedri come le unioni connesse di poliedri convessi e
2 Nota: non viviamo in un universo con quattro dimensioni spaziali, dunque non riusciamo a figurarci correttamente l’aspetto di un
politopo, ma la Matematica non è soggetta ai vincoli fisici cui invece è sottoposto chi la pratica.
Pagina 44 di 55
14
CONVESSITÀ E INVILUPPO CONVESSO
cosı̀ via. La frontiera di un poliedro, ossia la regione che separa l’interno del poliedro dall’esterno, è anche detta
superficie del poliedro ed è costituita da poligoni, detti facce del poliedro. Ognuna di queste facce ha un certo
numero di lati e vertici. I lati delle facce prendono anche il nome di spigoli del poliedro.
Esistono diversi poliedri notevoli, ossia interessanti per una ragione o per un’altra.
Il primo poliedro che studieremo sarà la piramide:
Definizione 89. Chiamiamo piramide l’inviluppo convesso di N ≥ 4 punti nello spazio, di cui esattamente N − 1
appartenenti ad uno stesso piano, detto piano di base. L’apice di una piramide (quello che è comunemente detto il
vertice della piramide) è il punto estraneo a tale piano, mentre la base è l’involucro convesso dei punti appartenenti
a tale piano. L’altezza di una piramide è la distanza dell’apice dal piano di base.
Notiamo che non è detto che la proiezione dell’apice sul piano di base cada internamente alla base, analogamente
alla situazione bidimensionale in cui un’altezza di un triangolo (ottusangolo) si colloca esternamente al triangolo. Un
discorso interessante riguarda il volume di una piramide. È abbastanza evidente che raddoppiando l’area della base,
oppure raddoppiando l’altezza, abbiamo un raddoppio del volume. Il volume di una piramide è dunque dato dal
prodotto tra l’area di base, l’altezza e una qualche costante. Problema: quale costante?
14.1
Il Principio di Cavalieri
Immaginiamo che la piramide della quale vogliamo calcolare il volume sia fatta di plastilina, o qualche altro materiale
rimodellabile. Possiamo procedere ad “affettare” tale piramide lungo piano molto vicini e paralleli alla base, per poi
procedere a risistemare le fette cosı̀ ottenute come meglio ci aggrada. Il processo non altera il volume della piramide
né la sua altezza, ma cambia secondo il nostro libero arbitrio la posizione della proiezione dell’apice sul piano di
base: tale informazione è perciò irrilevante ai fini del calcolo del volume. Possiamo inoltre rimodellare le singole
fette senza alterarne né lo spessore né il volume, ma cambiandone la forma. Supponendo che ogni fetta abbia sezione
quadrangolare, possiamo rimodellarla dandole l’aspetto di un disco circolare, e riassemblare le fette per dar vita ad
un cono.
Definizione 90. Chiamiamo cono l’involucro convesso di un cerchio e di un punto (apice) esterno al piano dove tale
cerchio (base) giace. Chiamiamo altezza del cono la distanza tra l’apice e il piano di base; diciamo che un cono è
retto se la proiezione dell’apice sul piano di base coincide con il centro del cerchio di base.
Pagina 45 di 55
14.1
Il Principio di Cavalieri
Abbiamo dunque che a parità di area della base (A) e a parità di altezza (h), una piramide ed un cono hanno lo stesso
volume, K · A · h.
D’altro canto, un cubo con spigolo di lunghezza l ha volume l3
ed è costituito da 6 piramidi (tante quante le facce) aventi
• base quadrata di area l2 ;
• altezza pari a 2l .
Di conseguenza, deve verificarsi:
l3 = 6 · K · l2 ·
l
2
da cui segue K = 13 .
Ciò dimostra che il volume di una piramide o di un cono è pari ad un terzo del prodotto tra l’area della base e
l’altezza3 . Un secondo problema che sorge spontaneo è quello di calcolare l’area della frontiera di un cono o di una
piramide, anche detta, semplicemente, superficie.
Un cono retto e un suo sviluppo piano
3 Una
dimostrazione alternativa passa dal calcolo diretto del volume di ogni fetta, cui segue l’applicazione dell’identità aritmetica:
12 + 22 + . . . + n2 =
n(n + 1)(2n + 1)
n3
≈
.
6
3
Pagina 46 di 55
14
CONVESSITÀ E INVILUPPO CONVESSO
Nel caso di un cono retto, avente per base un cerchio di raggio r, è opportuno considerare uno dei segmenti che
congiungono l’apice a un punto della circonferenza di base. La lunghezza di uno di questi segmenti è detta apotema
del cono, ed è usualmente indicata con la lettera a. Ovviamente, in virtù del Teorema di Pitagora, se l’altezza del cono
√
retto è h si ha a = h2 + r2 . Se immaginiamo di “staccare” la base del cono, quindi di tagliare la superficie laterale
rimanente lungo un segmento che congiunge l’apice con un punto della circonferenza di base, otteniamo lo sviluppo
piano rappresentato in figura. È perciò possibile “spiattellare” la superficie di un cono ottenendo una circonferenza di
raggio r (e dunque area πr2 ) e un settore circolare di raggio a. La lunghezza dell’arco di circonferenza relativo risulta
uguale alla lunghezza della circonferenza di base, cioè 2πr. D’altro canto, per il Principio di Cavalieri l’area di un
settore circolare è pari al semiprodotto tra il raggio e la lunghezza dell’arco di circonferenza associato: possiamo infatti
immaginare un settore circolare come generato dall’accostamento di miriadi di triangoli isosceli, aventi lati congruenti
di lunghezza pari al raggio del settore circolare, e basi le cui lunghezze, sommate tra loro, eguagliano la lunghezza
dell’arco di circonferenza. Ciò porta a concludere che la superficie di un cono retto di raggio r e altezza h è pari a:
p
1
A = πr2 + · 2πr · a = πr(r + a) = πr(r + r2 + h2 ).
2
A
Esercizio 91. ( ) Immaginiamo di avere un cono di altezza h e raggio r, con la proiezione dell’apice
che cade sulla circonferenza di base. Qual è la sua superficie?
Un altro poliedro notevole è il prisma:
Definizione 92. Dato un poligono convesso in un piano, determinato dai vertici A1 , A2 , . . . , An , e un suo traslato, determinato dai corrispondenti vertici B1 , B2 , . . . , Bn , chiamiamo prisma l’inviluppo convesso di tutti i precedenti vertici. Chiamiamo basi del prisma i poligoni determinati da A1 , A2 , . . . , An e
B1 , B2 , . . . , Bn ; chiamiamo altezza del prisma la distanza tra i
piani contenenti le basi e diciamo che un prisma è retto se il
segmento A1 B1 è perpendicolare al piano contenente una base.
Per il principio di Cavalieri, è ovvio che il volume di un prisma è pari al prodotto tra l’altezza e l’area di una base.
La superficie laterale (ossia quella non occupata dalle basi) di un prisma è data dalla somma delle aree di n parallelogrammi.
Se anche le basi sono parallelogrammi, il prisma si dice parallelepipedo; se tutte le facce sono rettangoli il prisma
si dice parallelepipedo; se tutte le facce sono rombi il prisma si dice romboedro; se tutte le facce sono quadrati il
prisma è semplicemente un cubo. Un caso limite di prisma retto è dato dal cilindro:
Definizione 93. Dato un cerchio Γ su un piano e un vettore v ortogonale a tale
piano, chiamiamo cilindro l’inviluppo convesso di Γ e Γ0 , dove Γ0 è il cerchio
ottenuto traslando Γ lungo v. Γ e Γ0 sono dette basi del cilindro e la lunghezza
di v è l’altezza.
Se il raggio di una circonferenza di base è r e l’altezza è h, un cilindro ha volume
V = πr2 h e superficie 2πr2 + 2πrh = 2πr(r + h).
Pagina 47 di 55
14.1
Il Principio di Cavalieri
Altri solidi notevoli sono il tronco di cono e il tronco di piramide, che si ottengono rimuovendo da un cono
o da una piramide (generalmente retti) un cono o una piramide più piccoli, attraverso un processo di sezione effettuato
con un piano parallelo alla base. Probabilmente, più semplice da raffigurarsi che da descriversi:
Una domanda piuttosto spontanea è quale sia il volume di questi solidi, se conosciamo le aree della basi e la distanza
tra queste. Studiamo prima il caso del tronco di cono, supponendo che le due basi abbiano raggi R ed r (con R > r)
e siano poste a distanza l (dunque l è altezza del tronco di cono). Supponiamo inoltre che h sia l’altezza del cono da
cui il tronco di cono è stato ricavato. Per il Teorema di Talete deve aversi:
h−l
h
=
r
R
e da ciò è semplice dedurre che si ha h =
lR
R−r
e (h − l) =
lr
R−r .
Il volume del cono originario è perciò:
π
π lR3
· R2 · h = ·
3
3 R−r
3
lr
e il volume del cono rimosso è pari a π3 · R−r
per ovvie ragioni di similitudine.
Segue che il volume del tronco di cono risulta pari a:
V =
πl R3 − r3
πl
·
=
· R2 + Rr + r2 .
3
R−r
3
Analogamente, un tronco di piramide avente basi di area A1 ed A2 ed altezza l risulta avere volume:
V =
p
l · A1 + A1 · A2 + A2
3
indipendentemente dalla forma delle basi.
Anche la superficie laterale di un tronco di cono o piramide può essere calcolata con tecniche analoghe (similitudini:
2
sottoponendo una superficie ad una omotetia di fattore Rr , la misura della superficie viene moltiplicata per Rr2 ),
a patto però che i coni in questione siano retti, in quanto il problema di calcolare la superficie laterale di un cono non
retto è al di là delle possibilità tecniche finora conquistate, dunque lo è anche quello di calcolare la superficie laterale
di un tronco di cono, se il cono originario non è retto.
Pagina 48 di 55
14
CONVESSITÀ E INVILUPPO CONVESSO
14.2
Poliedri regolari
Definizione 94. È detto poliedro regolare o solido platonico un poliedro che ha tutte le facce
congruenti a un poligono regolare.
Un risultato molto interessante in geometria solida è quello che stabilisce che i poliedri regolari sono soltanto cinque:
Tetraedro
4 facce triangolari
4 vertici
6 spigoli
Esaedro (cubo)
6 facce quadrate
8 vertici
12 spigoli
Ottaedro
8 facce triangolari
6 vertici
12 spigoli
Dodecaedro
12 facce pentagonali
20 vertici
30 spigoli
Icosaedro
20 facce triangolari
12 vertici
30 spigoli
Dato un poliedro regolare A, è possibile definirne un duale B nel seguente modo: i vertici di B sono i centri delle facce
di A e due vertici di B sono collegati da uno spigolo se e solo se le corrispondenti facce di A sono tra loro adiacenti.
È immediato verificare che il duale di un tetraedro è a sua volta un tetraedro, il duale di un cubo è un ottaedro (e
viceversa), il duale di un dodecaedro è un icosaedro (e viceversa). È inoltre evidente che un poliedro e il suo duale
hanno lo stesso numero di spigoli (S), mentre il processo di dualità scambia tra loro il numero di facce (F ) e il numero
di vertici (V ). Queste tre quantità sono tra loro collegate da ulteriori relazioni. Ad esempio, se ogni faccia ha N
vertici, su ogni faccia vi sono N spigoli, dunque il prodotto N · F è uguale al doppio del numero degli spigoli, in quanto
ogni spigolo appartiene esattamente a due facce. Analogamente, se da ogni vertice escono M spigoli, il prodotto M · V
è anch’esso uguale al doppio del numero degli spigoli, in quanto ogni spigolo ha esattamente due estremi. In sintesi:
N · F = 2 · S = M · V.
Vale inoltre una ulteriore relazione, estremamente profonda:
Teorema 95 (di Eulero). Per qualunque poliedro, regolare o meno, si verifica che:
F + V − S = 2.
Quelli riportati finora sono di fatto gli unici ingredienti necessari a dimostrare l’esistenza di soli 5 solidi platonici.
Per ognuno di questi, procediamo ora a calcolarne superficie, volume e raggi delle sfere inscritta e circoscritta,
supponendo che ogni spigolo abbia lunghezza unitaria. Il seguente lemma ci semplificherà molto la vita:
Lemma 96. Poiché un poliedro regolare A e il suo biduale A00 (sarebbe a dire il duale del duale) sono omotetici,
il rapporto dei loro volumi è il cubo del rapporto di dilatazione, e il volume di A0 , duale di A, è dato dalla media
geometrica del volume di A e di quello di A00 . Infatti, ogni due “passaggi” di dualità il volume viene moltiplicato per
una costante fissa, effettuando dunque un solo passaggio il volume viene moltiplicato per la radice quadrata di tale
costante.
Pagina 49 di 55
14.2
Poliedri regolari
Con Luca Pacioli arte e scienza si fondono: nel 1509 il frate francescano pubblica il De divina proporzione, che
incorpora il trattato sui solidi platonici De quinque corporibus regolaribus di Piero della Francesca, contenente
sessanta tavole di Leonardo da Vinci che rappresentano vari solidi in forma scheletrica. L’idea che ispira l’opera
di Pacioli è di una singolare modernità nel senso che si vuole sostenere, contro i pregiudizi umanistici, come la
scienza non sia solo tecnica ma anche “arte liberale”.
Nonostante l’evidente complessità dell’icosaedro, Luca Pacioli fu in grado di ideare una tecnica per costruirlo.
Alla base del suo metodo sta l’utilizzo di tre rettangoli aurei disposti su tre piani a due a due perpendicolari:
Avvalendosi della costruzione di Pacioli, non è difficile calcolare il volume dell’icosaedro.
Se questo ha spigolo unitario, i vertici di una faccia, nell’opportuno riferimento, hanno coordinate:
!
!
√
√ !
√
1+ 5 1
1
1+ 5
1+ 5 1
−
;− ;0 ,
− ; 0;
,
0; −
;
4
2
2
4
4
2
e il baricentro di tale faccia cade nel punto di coordinate:
√
√
√ !
3+ 5 3+ 5 3+ 5
−
;−
;
,
12
12
12
√
√
ad una distanza dall’origine pari a (3+ 125) 3 , raggio r della sfera inscritta.
L’icosaedro può essere visto come dato dall’accostamento di 20 piramidi aventi tale altezza e area di base pari a
dunque ha volume:
√
√ √
1
3 (3 + 5) 3
5
5√
V = 20 · ·
·
= +
5.
3 4
12
4 12
Il raggio della sfera circoscritta è invece dato dalla distanza di un vertice dall’origine:
s
s
√
√
6+2 5 1
5+ 5
R=
+ =
.
16
4
8
√
La superficie è quella di 20 triangoli equilateri di lato unitario, dunque A = 5 3.
p
√
Nell’icosaedro il rapporto tra il raggio della sfera circoscritta e quello della sfera inscritta è pari a 15 − 6 5:
per il precedente lemma, il volume del duale di un icosaedro di spigolo unitario è:
r
√
√ 1
5
1 5
·
·
(3
+
5)
=
65
+
29
5 .
p
√ 3
6 6
15 − 6 5 12
Pagina 50 di 55
√
3
4 ,
14
CONVESSITÀ E INVILUPPO CONVESSO
Tale poliedro duale è un dodecaedro. La lunghezza del suo spigolo è data dalla distanza tra due baricentri di facce
adiacenti nell’icosaedro di spigolo unitario, ossia dalla distanza tra i punti:
√
√
√ !
√
√ !
3+ 5 3+ 5 3+ 5
4+2 5
1+ 5
−
;−
;
e
−
; 0;
,
12
12
12
12
12
che è pari a
√
1+ 5
6 .
Segue che il volume di un dodecaedro di spigolo unitario è dato da:
√
15 + 7 5
V =
4
e che il raggio della sfera circoscritta è pari a:
R=
(3 +
√
√
√ √
5) 3
3 + 15
6
√ =
·
12
4
1+ 5
mentre quello della sfera inscritta è pari a:
s
s
√
5+ 5
1
5
11
6
√ ·
√ =
r=
·
+ √ .
8
8 8 5
15 − 6 5 1 + 5
p
√
La superficie è quella di venti pentagoni di lato unitario, pari a A = 3 25 + 10 5.
È interessante constatare che 8 dei 20 vertici di un dodecaedro determinano un cubo:
Passiamo ora al caso del tetraedro. Tutti i calcoli in questo caso sono molto agevolati dal fatto che i quattro punti
(1; 0; 0; 0),
(0; 1; 0; 0),
(0; 0; 1; 0),
(0; 0; 0; 1)
√
appartengono al sottospazio affine di R4 avente equazione x+y +z +w = 1 e sono a distanza 2 l’uno
Segue
q dall’altro.
2
1 1 1 1
3 2
che tale tetraedro ha centro nel punto di coordinate 4 ; 4 ; 4 ; 4 , raggio della sfera circoscritta pari a
+ 3 · 14 =
4
q
√
√
√
√
3
3
3
3
1 2
1 2
1
e
raggio
della
sfera
inscritta
pari
a
3
·
+
=
,
dunque
volume
pari
a
4
·
·
2
·
2
12
4
6
4
18 = 3 .
Segue che per un tetraedro di spigolo unitario si ha:
1
V = √ ,
6 2
A=
√
r
3,
R=
Pagina 51 di 55
3
,
8
1
r= √ .
2 6
14.2
Poliedri regolari
Passiamo ora a cubo e ottaedro. Chiaramente, il poliedro con vertici a coordinate (±1, ±1, ±1) è un cubo con spigolo
√
di lunghezza 2, raggio della sfera inscritta pari a 1 e raggio della sfera circoscritta pari a 3. Il duale è un ottaedro
√
con spigolo di lunghezza 2, raggio della sfera circoscritta pari a 1 e raggio della sfera inscritta pari a √13 .
Segue che per un cubo di spigolo unitario si ha:
√
3
1
V = 1, A = 6, R =
, r= ,
2
2
mentre per un ottaedro di spigolo unitario si ha:
√
√
2
V =
, A = 2 3,
3
√
2
,
2
R=
1
r= √ .
6
Riassumendo, il quadro generale per i poliedri regolari di spigolo unitario è il seguente:
Tetraedro
V =
A=
R=
r=
1
√
6 2
√
3
q
3
8
1
√
2 6
Esaedro (cubo)
Ottaedro
V =1
V =
√
A=6
R=
r=
√
√
3
2
1
2
R=
r=
Dodecaedro
V =
2
2
√1
6
Icosaedro
√
15+7 5
4
V =
p
√
A = 3 25 + 10 5
√
2
3
√
A=2 3
5
12 (3
+
√
√
A=5 3
q √
R = 5+8 5
√
R = 3+4 15
q
√
r = 58 + 811
5
√
r=
5)
√
15+ 27
12
Realizzando esplicitamente le configurazioni dei vertici in R3 , quindi avvalendosi di prodotti scalari e funzioni trigonometriche inverse, è inoltre possibile verificare che gli angoli tra due facce adiacenti (anche detti angoli diedri o angoli
diedrali ) sono i seguenti:
Tetraedro:
Cubo:
Ottaedro:
Dodecaedro:
Icosaedro:
70◦ 310 4300
90◦
109◦ 280 1600
116◦ 330 5400
138◦ 110 2200
Il Teorema di rigidità di Cauchy stabilisce che lo scheletro di un poliedro regolare, come quello di qualunque
poliedro convesso, non è deformabile (come invece lo è, ad esempio, lo scheletro di un quadrilatero nel piano). Inoltre
lo scheletro di un poliedro regolare, come di un qualunque poliedro che abbia tutti i vertici sulla frontiera di un insieme
convesso (come, ad esempio, una sfera), si può rappresentare attraverso un grafo planare:
Pagina 52 di 55
14
CONVESSITÀ E INVILUPPO CONVESSO
14.3
Sfera e toro
Teorema 97 (Pappo-Guldino). Data A, regione limitata del piano cartesiano contenuta nel semipiano superiore
y ≥ 0, il solido generato della rotazione di A attorno all’asse delle ascisse ha volume pari all’area di A moltiplicata
per la lunghezza della circonferenza percorsa dal baricentro di A. Analogamente, se γ è una curva chiusa semplice
contenuta nel semipiano superiore, la superficie del solido generato dalla rotazione di γ attorno all’asse delle ascisse
è data dal prodotto tra la lunghezza di γ e la lunghezza della circonferenza percorsa dal baricentro di γ.
Una dimostrazione rigorosa di questo importante risultato necessita di strumenti di calcolo infinitesimale (anche se
rudimentali). In ogni caso esso può essere visto come una generalizzazione degli argomenti utilizzati per determinare
superficie e volume di un cono, essenzialmente soltanto il Principio di Cavalieri. Notiamo che la costante 31 che
figura nel volume di un cono può essere interpretata, a questo punto, come semplice conseguenza del fatto che, nel
piano, un triangolo di vertici A, B, C ha baricentro in A+B+C
. Il Teorema di Pappo-Guldino fa luce sul fatto che la
3
determinazione del volume o della superficie di un solido di rotazione è equivalente al problema della determinazione
di un baricentro. In particolare, i seguenti problemi sono lo stesso problema, per quanto non lo sembrino:
Esercizio 98. Qual è il volume di una sfera di raggio R?
Esercizio 99. Dov’è collocato il baricentro di un semicerchio di raggio R?
Esercizio 100. Qual è la superficie di una sfera di raggio R?
Esercizio 101. Dov’è collocato il baricentro di una semicirconferenza di raggio R?
Il legame tra il primo e terzo quesito è sempre dato dal Principio di Cavalieri. Se immaginiamo di ripartire la superficie
di una sfera in triangoli molto piccoli, il volume risulta pari alla somma dei volumi di tante piramidi. Di conseguenza,
se la superficie di una sfera è pari a CS · R2 (per una qualche costante CS da determinare) e il suo volume è pari a
CV · R3 , si ha CS = 3 · CV .
Facendo invece ruotare un cerchio di raggio r attorno ad un asse esterno,
complanare, a distanza R dal centro del cerchio, si ottiene un solido “ciambelliforme” denominato toro. Attraverso il Teorema di Pappo-Guldino, non
è difficile calcolarne superficie e volume. Si ha:
V = 2π 2 r2 R,
A = 4π 2 rR.
Quasi paradossalmente, il caso della sfera è più spinoso.
Pagina 53 di 55
14.3
Sfera e toro
Il volume della sfera può essere facilmente determinato attraverso un’argomentazione dovuta ad Archimede. Possiamo immaginare una sfera
di raggio R e due coni con raggio di base e altezza pari ad R, disposti
come in figura. Quello che accade è che ogni sezione effettuata con un
piano orizzontale determina due cerchi, uno relativo alla sfera e l’altro
al cono, aventi una costante somma delle aree. Per il Principio di Cavalieri si ha perciò che il volume della sfera, sommato al volume del cono,
eguaglia il volume di un cilindro di altezza 2R e raggio di base R.
Da semplici calcoli segue che il volume della sfera risulta pari a:
V =
4
π R3 ,
3
dunque la superficie di una sfera di raggio R è pari a A = 4πR2 e il
baricentro di un semicerchio di raggio R cade a distanza 4R
3π dal centro
del semicerchio, mentre il baricentro di una semicirconferenza di raggio
R
R cade a distanza 2π
dal centro della semicirconferenza.
Esercizio 102. Nel piano cartesiano, un trapezio ha vertici nei punti O(0; 0), A(2; 0), B(1; 1) e C(0; 1).
Si determini la collocazione del suo baricentro G attraverso il Teorema di Pappo-Guldino.
Dimostrazione. La richiesta del problema può suonare bizzarra, ma è volta a far luce su un aspetto interessante. Molto
spesso in Matematica risulta fruttuoso trasportare le nostre costruzioni in uno spazio più grande di quello originario
(un caso eclatante è quello del Teorema di Desargues in geometria proiettiva, ma lo è anche il processo di estensione
Q 7→ R 7→ C), e l’efficacia di tale approccio “creativo” risiede in una briciola d’inappuntabile buon senso: se abbiamo
più spazio, siamo più liberi di muoverci. Tornando al problema, se facciamo ruotare il trapezio attorno all’asse delle
ordinate otteniamo un tronco di cono con altezza 1 e raggi delle circonferenze di base pari rispettivamente a 2 e a 1.
3
Il volume di tale tronco di cono è π3 22 + 2 · 1 + 12 = 7π
3 . Dato che l’area del trapezio è 2 , l’ascissa del baricentro è
7
9 . Analogamente, facendo ruotare il trapezio attorno all’asse delle ascisse si ottiene un solido dato dall’accostamento
4
di un cilindro e di un cono, avente volume pari a π + π3 = 4π
3 , dunque l’ordinata del baricentro è 9 .
Si ha perciò che il baricentro giace in G 79 ; 49 .
Non a caso, se denominiamo con M il punto medio di OA, abbiamo
che il baricentro del trapezio giace a 31 della strada tra il baricentro
del quadrato OM BC e il baricentro del triangolo M AB: infatti
il quadrato OM BC ha area doppia rispetto a quella del triangolo
M AB.
Sarebbe stato facile determinare la posizione di G anche sfruttando il fatto che tutte le rette passanti da G
devono tagliare il trapezio in due parti aventi la stessa area, 43 .
Sulla superficie di una sfera è possibile definire una geometria dove il quinto postulato (data una retta r e un punto
P 6∈ r, esiste un’unica parallela ad r passante da P ) cessa di essere valido. In particolare, è possibile ri-definire il
concetto di segmento attraverso quello di geodetica (percorso di minima lunghezza). Sulla sfera, tutte le geodetiche sono porzioni della frontiera di qualche cerchio massimo, ossia di qualche cerchio che passa per il centro della
sfera. Un triangolo sferico è una porzione di superficie sferica delimitata da tre punti A, B, C e dalle geodetiPagina 54 di 55
14
CONVESSITÀ E INVILUPPO CONVESSO
che (lati) tra A e B, B e C, C ed A. Analogamente al caso euclideo, i lati confluenti in un vertice determinano,
sulla superficie, un angolo con una certa ampiezza. Su una sfera, tuttavia, non esistono circonferenze massime
che non si intersechino, dunque la geometria sferica è un esempio di geometria dove non esistono rette parallele.
In particolare, non è più valido il Teorema dell’angolo
esterno, dunque la somma degli angoli interni di un triangolo sferico non è costante, ma ciò non significa che non
si presentino situazioni interessanti. Nel caso dei triangoli
sferici, infatti, si ha correlazione diretta tra l’eccesso angolare (definito come la somma degli angoli interni, meno
un angolo piatto) e l’area:
A = (α + β + γ − 180◦ ) ·
πR2
180◦
In particolare, sulla superficie sferica esistono diversi triangoli curvilinei che hanno tre angoli retti, ma ognuno di
questi ha area esattamente uguale ad 81 della superficie
della sfera.
Jacopo D’Aurizio
[email protected]
http://www.matemate.it
Pagina 55 di 55

30.-Geometria euclidea

Documenti correlati

Prodotti

Supporto

30.-Geometria euclidea

Documenti correlati

Aggiungere questo documento alla raccolta (s)

Aggiungere questo documento salvato

Suggeriscici come migliorare StudyLib