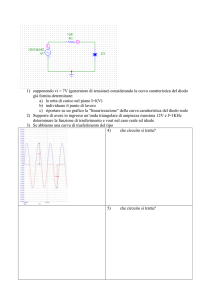
caricato da
info
PROPRIETÀ DELLE CURVE PIANE

ALCUNE PROPRIETÀ
GEOMETRICHE
INTRINSECHE
DELLE CURVE PIANE
Definizione e calcolo delle principali proprietà geometriche intrinseche delle
curve piane quali lunghezza d’arco, versore tangente, versore normale principale, curvatura, raggio di curvatura, pendenza, copendenza, versore normale
interno. Sono analizzate curve piane rappresentate in forma parametrica, cartesiana esplicita, polare e cartesiana implicita.
Marco Busato
1.
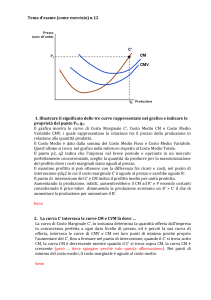
LE PROPRIETA’ GEOMETRICHE INTRINSECHE DELLE CURVE PIANE
Sia γ una curva piana regolare che rispetto ad un arbitrario sistema di coordinate cartesiane ortogonali
{0, x, y} fissato nel suo piano risulti rappresentata dalle equazioni parametriche:
x = x(t )
y = y (t )
1.1
dove si suppone t ∈ [ ta , tb ] ed x(t ), y (t ) due assegnate funzioni di classe C n [ ta , tb ], n ≥ 2 . La situazione descritta è mostrata in Figura 1.1.
Figura 1.1
Se nella 1.1 le funzioni x(t ), y (t ) vengono sostituite dalle funzioni x (t ) = x[ f (t )], y (t ) = y[ f (t )]
dove f (t ) è una funzione qualsiasi opportunamente regolare ( f (t ) deve essere tale che x (t ), y (t ) ∈
C n [ f −1 (ta ), f −1 (tb ) ], n ≥ 2 ), le equazioni 1.1 descrivono ancora la medesima curva γ . La trasformazione x(t ) → x (t ) , y (t ) → y (t ) cambia infatti solo l’ordine dei punti che costituiscono γ . L’operazione x(t ) → x (t ) , y (t ) → y (t ) è detta una riparametrizzazione di γ e le proprietà geometriche di
γ che non dipendono dalla parametrizzazione utilizzata per rappresentarla, e che quindi dipendono
solo dalla forma di γ , sono le cosiddette proprietà geometriche intrinseche della curva stessa. Esse,
per una curva dotata della regolarità da noi ipotizzata (almeno del secondo ordine) sono quelle qui di
seguito definite.
Definizione 1.1 Definizione di elemento di lunghezza d’arco
Si dice elemento di lunghezza d’arco della curva γ la grandezza ds così definita ∀t ∈ [ ta , tb ] :
=
ds
dx 2 + dy 2
1.2
dove dx e dy sono i differenziali delle funzioni x(t ) e y (t ) . Nella 1.2 si deve quindi considerare:
dx = x (t ) dt
;
dy = y (t ) dt
1.3
Il significato di ds è mostrato in Figura 1.2.
1
Figura 1.2
Definizione 1.2 Definizione di versore tangente e versore normale principale
Posto:
=
r x(t ) ˆi + y (t ) ˆj
1.4
si dicono rispettivamente versore tangente e versore normale principale alla curva γ i versori t̂ ed
n̂ così rispettivamente definiti ∀t ∈ [ ta , tb ] in corrispondenza dei quali la relazione esiste:(1)
r
tˆ =
| r |
;
tˆ
nˆ =
| tˆ |
1.5
dove con r e t̂ si sono rispettivamente indicate le derivate rispetto al parametro t del vettore r e del
versore t̂ . Il versore t̂ esiste in ogni punto della curva γ (infatti r ≠ 0 ∀t ∈ [ ta , tb ] ) e risulta orien
tato nel senso delle t crescenti. Il versore n̂ esiste in tutti i punti della curva γ ove tˆ ≠ 0 , cioè ad
eccezione dei punti di flesso, in corrispondenza dei quali subisce una discontinuità del verso. Esso,
ovunque esiste, risulta ortogonale a t̂ e sempre orientato verso centro del cerchio osculatore a γ (cioè
dalla parte del piano in cui la curva γ presenta la concavità). Si noti che a causa di quest’ultima
proprietà di n̂ , la coppia ordinata ( t̂ , n̂ ) non può costituire una base ortonormale sempre sinistrogira
o sempre destrogira lungo γ .(2) In Figura 1.3 sono riportati i versori t̂ ed n̂ relativi a due generici
punti di γ così da mettere in evidenza come in presenza di flessi il versore n̂ presenti necessariamente
una discontinuità del verso e la coppia ordinata ( t̂ , n̂ ) non posa costituire una base ortonormale
sempre sinistrogira o sempre destrogira lungo γ .
1)
In questo scritto seguiamo l’impostazione classica, utilizzata anche in [1]. In [2] è invece usata un’altra definizione di
versore normale principale. Per maggiori dettagli si rimanda alla Nota 5.
2)
Ricordiamo che una tripletta ordinata di versori ortogonali ( eˆ1 , eˆ 2 , eˆ 3 ) si dice sinistrogira se un osservatore posto come
ê3 per fare sovrapporre ê1 ad ê 2 (tenuto fisso) con una rotazione di angolo ϕ < π nel piano formato da eˆ1 , eˆ 2 , deve
ruotare ê1 in senso antiorario. Nel caso della coppia ( t̂ , n̂ ) il terzo versore di identifica con kˆ = ˆi ∧ ˆj .
2
Figura 1.3
Definizione 1.3 Definizione di curvatura e raggio di curvatura
Si dicono rispettivamente curvatura e raggio di curvatura della curva γ la grandezza non negativa
κ e ρ , una reciproca dell’altra, così definite ∀t ∈ [ ta , tb ] :(3)
| tˆ |
κ=
| r |
;
ρ=
1
1.6
κ
Il raggio di curvatura ρ è il raggio del cerchio osculatore alla curva γ , come mostrato in Figura 1.4.
Figura 1.4
Definizione 1.4 Definizione di pendenza
Si dice pendenza della curva γ l’angolo orientato φ (positivo se antiorario) fra l’asse x ed il versore
tangente t̂ , cioè l’angolo definito dalla seguente relazione ∀t ∈ [ ta , tb ] :
In generale, si può dimostrare che una curva di uno spazio D-dimensionale (D > 1) possiede D − 1 curvature generalizzate κ i . Tali curvature sono definite da una relazione ricorrente che nel caso delle curve piane fornisce per κ la seguente
espressione: κ =
| < tˆ | nˆ > | / | r | dove con < tˆ | nˆ > si è indicato il prodotto scalare fra t̂ ed n̂ .
3)
3
< tˆ | ˆi >
cos(φ ) =
⇒
φ= arccos(< tˆ | ˆi >)
1.7
dove con < tˆ | ˆi > si è indicato il prodotto scalare fra t̂ ed î . L’angolo φ si può anche definire mediante la seguente relazione (quando dx ≠ 0 ):
tan(φ ) =
dy
dx
⇒
dy
dx
φ = arctan
1.8
dove dx e dy sono i differenziali delle funzioni x(t ) e y (t ) . Il significato di φ è mostrato in Figura
1.5.
Figura 1.5
Definizione 1.5 Definizione di copendenza
Si dice copendenza della curva γ l’angolo orientato ψ (positivo se antiorario) fra l’asse y ed il versore
tangente t̂ , cioè l’angolo definito dalla seguente relazione ∀t ∈ [ ta , tb ] :(4)
cos(ψ ) =
< tˆ | ˆj >
⇒ ψ= arccos(< tˆ | ˆj >)
1.9
dove con < tˆ | ˆj > si è indicato il prodotto scalare fra t̂ e ĵ . L’angolo ψ si può anche definire mediante la seguente relazione (quando dy ≠ 0 ):
tan(ψ ) =
dx
dy
dx
⇒ ψ = arctan
dy
1.10
dove dx e dy sono i differenziali delle funzioni x(t ) e y (t ) . Il significato di ψ è mostrato in Figura
1.6.
Chiaramente=
ψ π / 2 − φ per cui sarebbe superfluo definire la copendenza una proprietà intrinseca della curva γ .
Tuttavia in numerose applicazioni pratiche l’angolo ψ riveste un particolare interesse per cui è utile avere una espressione
esplicita di ψ . Si deve ad esempio fare riferimento all’angolo ψ nel calcolo del coefficiente di rifrazione geodetica in
funzione dell’indice di rifrazione atmosferica.
4)
4
Figura 1.6
Osservazione 1.1 Versore normale interno
Come si è detto, il versore n̂ presenta una discontinuità del verso in corrispondenza degli eventuali
punti di flesso γ . Il versore û , parallelo ad nˆ , che non presenta questa discontinuità lungo γ , ed è
di conseguenza tale da formare con t̂ una base ortonormale sempre sinistrogira per ogni punto di γ ,
si ottiene a partire da n̂ per mezzo della relazione seguente:(5)
+nˆ se φ > 0
uˆ =
−nˆ se φ < 0
1.11
La differenza fra i versori û ed n̂ è mostrata in Figura 1.7 mentre in Figura 1.8 è mostrato come la
coppia ordinata ( t̂ , û ) risulti una base ortonormale sempre sinistrogira per ogni punto di γ . Si noti
se γ fosse una curva chiusa antioraria, û sarebbe rivolto sempre verso la regione di piano interna γ .
Per tale ragione esso è spesso indicato come versore normale interno a γ .
Figura 1.7
Figura 1.8
5)
Come si è detto in Nota 1, in questo scritto seguiamo l’impostazione classica, utilizzata anche in [1]. In [2] viene usata
un’altra impostazione e precisamente il versore che noi abbiamo chiamato versore normale principale n̂ , in [2] viene
indicato con k̂ e chiamato versore curvatura, mentre quello che noi abbiamo indicato con û , in [2] è chiamato versore
normale principale ed indicato con n̂ .
5
Osservazione 1.2
Differenti possibili definizioni delle grandezze precedentemente introdotte e relazioni che fra esse intercorrono
Le varie grandezze sopra introdotte sono suscettibili di definizioni equivalenti e risultano fra loro
legate. In particolare, si può dimostrare che:
| r | =
ds
dt
;
dr
tˆ =
ds
;
nˆ =
1 d tˆ
κ ds
;
κ=
dφ
ds
1.12
Chiaramente, a partire dalle relazioni sopra riportate, eventualmente con l’ausilio di quelle precedentemente introdotte, si possono ottenere altre relazioni fra le grandezze considerate. Si può inoltre
passare agevolmente dalla derivazione rispetto ad s a quella rispetto a t e viceversa, avvalendosi della
formula:
ds
=
dt
x 2 + y 2
1.13
Così, potendosi scrivere per noti teoremi del calcolo differenziale:
d dt d
=
ds ds dt
1.14
è facile vedere che:
κ=
dφ
ds
⇒
κ=
| φ |
1.15
x 2 + y 2
Concludiamo il paragrafo osservando che indicata con dα l’ampiezza dell’angolo infinitesimo formato fra i vettori tangenti alla curva γ in due suoi punti infinitamente vicini, risulta che ∀t ∈ [ ta , tb ] :
ρ=
ds
dα
⇒
ds = ρ dα
1.16
La 1.16 si può facilmente comprendere facendo riferimento alla Figura 1.9, oppure osservando, come
ugualmente mostrato in Figura 1.9, che dα = | dφ | ed utilizzando poi l’ultima delle 1.12.
Figura 1.9
6
2.
FORMA ESPLICITA DELLE PROPRIETA’ GEOMETRICHE INTRINSECHE DELLE
CURVE PIANE NEL CASO DI CURVE RAPPRESENTATE IN FORMA PARAMETRICA
Qui di seguito riportiamo le formule esplicite di uso pratico per le proprietà geometriche intrinseche
di una curva piana γ regolare almeno fino al secondo ordine nel caso in cui la curva sia rappresentata
in forma parametrica in un sistema di coordinate cartesiane ortogonali {0, x, y} fissato nel suo piano.
Supponiamo cioè che γ sia rappresentata nella forma:
x = x(t )
y = y (t )
2.1
dove si suppone t ∈ [ ta , tb ] ed x(t ), y (t ) due assegnate funzioni di classe C n [ ta , tb ], n ≥ 2 .
2.1 Lunghezza dell’arco
La lunghezza dell’arco ds fra due punti infinitamente vicini della curva γ, P = ( x(t ), y (t )) ) e
P' =
( x(t + dt ), y (t + dt )) è data da:
x (t ) 2 + y (t ) 2 d t
=
ds
2.2
La lunghezza dell’arco s12 fra due punti qualsiasi di γ, P1 = ( x(t1 ), y (t1 ) ) e P2 = ( x(t2 ), y (t2 ) ) si
ottiene integrando la 2.2 da t 1 e t 2 . Si ha quindi:
t2
=
s12
⌠
⌡
x (t ) 2 + y (t ) 2 dt
2.3
t1
2.2 Versore tangente e versore normale
Il versore tangente t̂ ed il versore normale principale n̂ a γ in un suo punto qualsiasi P = ( x(t ), y (t ))
sono le funzioni vettoriali così rispettivamente definite per t ∈ [ ta , tb ] :
=
tˆ(t )
nˆ (t ) = ±
x (t )
x (t ) + y (t )
2
2
ˆi +
y (t )
x (t ) 2 + y (t ) 2
y (t )
x (t ) + y (t )
ˆi
2
2
ˆj
x (t )
x (t ) 2 + y (t ) 2
2.4
ˆj
2.5
x(t ) y (t ) − x (t )
y (t ) > 0 , mentre i segni inferiori si deNella 2.5, i segni superiori si devono usare se
vono usare se
x(t ) y (t ) − x (t )
y (t ) < 0 .
2.3 Curvatura e raggio di curvatura
La curvatura κ ed il raggio di curvatura ρ della curva γ in un suo punto qualsiasi P = ( x(t ), y (t ))
sono le funzioni scalari non negative così rispettivamente definite per t ∈ [ ta , tb ] :
7
κ (t ) =
x(t ) y (t ) − x (t )
y (t )
( x(t )
2
+ y (t ) 2 )
ρ (t ) =
;
3/2
( x(t )
2
+ y (t ) 2 )
3/2
2.6
x(t ) y (t ) − x (t )
y (t )
2.4 Pendenza e copendenza
La pendenza φ e la copendenza ψ della curva γ in un suo punto qualsiasi P = ( x(t ), y (t )) sono le
funzioni scalari così rispettivamente definite per t ∈ [ ta , tb ] :
x (t ) 2 + y (t ) 2
φ (t ) = arccos
x (t )
x (t ) 2 + y (t ) 2
ψ (t ) = arccos
y (t )
y (t )
x (t )
oppure
φ (t ) = arctan
oppure
ψ (t ) = arctan
x (t )
y (t )
(se x (t ) ≠ 0 )
2.7
(se y (t ) ≠ 0 )
2.8
E’ utile osservare che:
φ(t ) = −
x(t ) y (t ) − x (t )
y (t )
2
2
x (t ) + y (t )
⇒
> 0
< 0
φ(t )
se
x(t ) y (t ) − x (t )
y (t ) < 0
se
x(t ) y (t ) − x (t )
y (t ) > 0
2.9
La 2.9 consente di rappresentare esplicitamente il versore normale interno û .
2.5 Versore normale interno
Il versore normale interno û a γ in un suo punto qualsiasi P = ( x(t ), y (t )) è la funzione vettoriale
così definita per t ∈ [ ta , tb ] :
y (t )
x (t )
ˆi +
ˆj
uˆ (t ) =
−
x (t ) 2 + y (t ) 2
x (t ) 2 + y (t ) 2
2.10
8
3.
FORMA ESPLICITA DELLE PROPRIETA’ GEOMETRICHE INTRINSECHE DELLE
CURVE PIANE NEL CASO DI CURVE RAPPRESENTATE IN FORMA CARTESIANA
ESPLICITA
Qui di seguito riportiamo le formule esplicite di uso pratico per le proprietà geometriche intrinseche
di una curva piana γ regolare almeno fino al secondo ordine nel caso in cui la curva sia rappresentata
in forma cartesiana esplicita in un sistema di coordinate cartesiane ortogonali {0, x, y} fissato nel suo
piano. Supponiamo cioè che γ sia rappresentata nella forma:
y = f ( x)
3.1
dove si suppone x ∈ [ xa , xb ] ed f ( x) una assegnata funzione di classe C n [ xa , xb ], n ≥ 2 . La situazione descritta è mostrata in Figura 3.1.
Figura 3.1
Poiché la 3.1 si può riscrivere nella forma seguente (del tipo 2.1):
x = t
y = f (t )
3.2
con t ∈ [ xa , xb ] , le espressioni esplicite delle proprietà geometriche intrinseche di γ si possono immediatamente ottenere da quelle riportate nel precedente paragrafo eseguendo in esse le sostituzioni
formali:
t→x
3.3
x(t ) → x
x (t ) → 1
x(t ) → 0
3.4
y (t ) → f ( x)
y (t ) → f '( x)
y (t ) → f ''( x)
3.5
3.1 Lunghezza dell’arco
La lunghezza dell’arco ds fra due punti infinitamente vicini della curva γ, P = ( x, f ( x)) ) e
P' =
( x + dx, f ( x + dx)) è data da:
9
ds
=
1 + f '( x) 2 d x
3.6
La lunghezza dell’arco s12 fra due punti qualsiasi di γ, P1 = ( x1 , y ( x1 ) ) e P2 = ( x 2 , f ( x2 ) ) si ottiene
integrando la 2.2 da x1 e x 2 . Si ha quindi:
x2
=
s12
⌠
⌡
1 + f '( x) 2 d x
3.7
x1
3.2 Versore tangente e versore normale
Il versore tangente t̂ ed il versore normale principale n̂ a γ in un suo punto qualsiasi P = ( x, f ( x))
sono le funzioni vettoriali così rispettivamente definite per x ∈ [ xa , xb ] :
1
=
tˆ( x)
1 + f '( x)
nˆ ( x) = ±
ˆi +
2
f '( x)
1 + f '( x)
2
f '( x)
1 + f '( x)
ˆi
2
ˆj
1
1 + f '( x)
2
3.8
ˆj
3.9
Nella 3.9, i segni superiori si devono usare se f ''( x) < 0 , mentre i segni inferiori si devono usare se
f ''( x) > 0 .
3.3 Curvatura e raggio di curvatura
La curvatura κ ed il raggio di curvatura ρ della curva γ in un suo punto qualsiasi P = ( x, f ( x)) sono
le funzioni scalari non negative così rispettivamente definite per x ∈ [ xa , xb ] :
κ ( x) =
( 1 + f '( x) )
ρ ( x) =
2 3/2
f ''( x)
( 1 + f '( x)2 )
3/2
;
3.10
f ''( x)
3.4 Pendenza e copendenza
La pendenza φ e la copendenza ψ della curva γ in un suo punto qualsiasi P = ( x, f ( x)) sono le
funzioni scalari così rispettivamente definite per x ∈ [ xa , xb ] :
1 + f '( x) 2
φ ( x) = arccos
1
1 + f '( x) 2
ψ ( x) = arccos
f '( x)
oppure
φ ( x) = arctan ( f '( x) )
oppure
ψ ( x) = arctan
1
f '( x)
E’ utile osservare che:
10
( ∀x ∈ [ xa , xb ] )
3.11
(se f '( x) ≠ 0 )
3.12
φ '( x) =
f ''( x)
1 + f '( x) 2
⇒
> 0
< 0
φ '( x)
se f ''( x) > 0
se f ''( x) < 0
3.13
La 3.10 consente di rappresentare esplicitamente il versore normale interno û .
2.5 Versore normale interno
Il versore normale interno û a γ in un suo punto qualsiasi P = ( x, f ( x)) è la funzione vettoriale così
definita per x ∈ [ xa , xb ] :
f '( x)
ˆi +
uˆ ( x) =
−
2
1 + f '( x)
1
1 + f '( x)
2
ˆj
3.14
11
4. FORMA ESPLICITA DELLE PROPRIETA’ GEOMETRICHE INTRINSECHE DELLE
CURVE PIANE NEL CASO DI CURVE RAPPRESENTATE IN FORMA POLARE
Qui di seguito riportiamo le formule esplicite di uso pratico delle proprietà geometriche intrinseche
di una curva piana γ , regolare almeno fino al secondo ordine, nel caso in cui la curva sia rappresentata
in forma polare in un sistema di coordinate cartesiane ortogonali {0, x, y} fissato nel suo piano. Supponiamo cioè che γ sia rappresentata nella forma:
r = r (θ )
4.1
dove si suppone θ ∈ [ θ a , θb ] ed r (θ ) una assegnata funzione di classe C n [ θ a , θb ], n ≥ 2 . La situazione descritta è mostrata in Figura 4.1.
Figura 4.1
Poiché fissato un sistema di coordinate cartesiane ortogonali {0, x, y} con asse x coincidente con
l’asse polare del sistema, la 3.1 si può riscrivere nella forma seguente (del tipo 2.1):
x = r (θ ) cos(θ )
y = r (θ ) sin(θ )
4.2
con θ ∈ [ θ a , θb ] , le espressioni esplicite delle proprietà geometriche intrinseche di γ si possono
immediatamente ottenere da quelle riportate nel Paragrafo 2 eseguendo in esse le sostituzioni formali:
t →θ
4.3
x(t ) → r (θ ) cos(θ )
x (t ) →
d
( r (θ ) cos(θ ) )
dθ
x(t ) →
d2
( r (θ ) cos(θ ) )
dθ 2
4.4
y (t ) → r (θ ) sin(θ )
y (t ) →
d
( r (θ ) sin(θ ) )
dθ
y (t ) →
d2
( r (θ ) sin(θ ) )
dθ 2
4.5
Nel seguito la derivata rispetto a θ verrà indicata con l’apice e rappresenteremo i versori tˆ, nˆ , uˆ in
termini dei versori ˆi , ˆj degli assi cartesiani. Le espressioni di tˆ, nˆ , uˆ in termini dei versori base
12
eˆ r , eˆ θ di un sistema polare {O, r , θ } con origine ed asse polare coincidente rispettivamente con
l’origine e l’asse x del sistema {0, x, y}, sono riportate in Osservazione 4.1.
4.1 Lunghezza dell’arco
La lunghezza dell’arco ds fra due punti infinitamente vicini della curva γ, P = (θ , r (θ )) ) e
P' =
(θ + dθ , r (θ + dθ )) è data da:
r (θ ) 2 + r '(θ ) 2 dθ
ds
=
4.6
La lunghezza dell’arco s12 fra due punti qualsiasi di γ, P1 = ( θ1 , r (θ1 ) ) e P2 = ( θ 2 , r (θ 2 ) ) si ottiene
integrando la 2.2 da θ 1 e θ 2 . Si ha quindi:
θ2
=
s12
⌠
⌡
r (θ ) 2 + r '(θ ) 2 d θ
4.7
θ1
4.2 Versore tangente e versore normale
Il versore tangente t̂ ed il versore normale principale n̂ a γ in un suo punto qualsiasi P = (θ , r (θ ))
sono le funzioni vettoriali così rispettivamente definite per θ ∈ [ θ a , θb ] :
tˆ(θ )
− r (θ ) sin(θ ) + r '(θ ) cos(θ ) ˆ r (θ ) cos(θ ) + r '(θ ) sin(θ ) ˆ
i+
j
r (θ ) 2 + r '(θ ) 2
r (θ ) 2 + r '(θ ) 2
nˆ (θ ) = ±
4.8
r (θ ) cos(θ ) + r '(θ ) sin(θ ) ˆ − r (θ ) sin(θ ) + r '(θ ) cos(θ ) ˆ
i
j
r (θ ) 2 + r '(θ ) 2
r (θ ) 2 + r '(θ ) 2
4.9
Nella 2.5, i segni superiori si devono usare se r (θ ) 2 + 2r '(θ ) 2 − r (θ ) r ''(θ ) < 0 , mentre i segni inferiori
si devono usare se r (θ ) 2 + 2r '(θ ) 2 − r (θ ) r ''(θ ) > 0 .
4.3 Curvatura e raggio di curvatura
La curvatura κ ed il raggio di curvatura ρ della curva γ in un suo punto qualsiasi P = (θ , r (θ )) sono
le funzioni scalari non negative così rispettivamente definite per θ ∈ [ θ a , θb ] :
κ (θ ) =
r (θ ) 2 + 2r '(θ ) 2 − r (θ ) r ''(θ )
( r (θ )
2
+ r '(θ ) 2 )
3/2
ρ (θ ) =
;
( r (θ )
2
+ r '(θ ) 2 )
3/2
r (θ ) 2 + 2r '(θ ) 2 − r (θ ) r ''(θ )
4.10
4.4 Pendenza e copendenza
La pendenza φ e la copendenza ψ della curva γ in un suo punto qualsiasi P = (θ , r (θ )) sono le
funzioni scalari così rispettivamente definite per θ ∈ [ θ a , θb ] :
13
− r (θ ) sin(θ ) + r '(θ ) cos(θ )
r (θ ) 2 + r '(θ ) 2
4.11
r (θ ) cos(θ ) + r '(θ ) sin(θ )
r (θ ) 2 + r '(θ ) 2
4.12
φ (θ ) = arccos
ψ (θ ) = arccos
In alternativa alle 4.11 e 4.12 si possono rispettivamente usare le seguenti relazioni:
r (θ ) cos(θ ) + r '(θ ) sin(θ )
− r (θ ) sin(θ ) + r '(θ ) cos(θ )
se − r (θ ) sin(θ ) + r '(θ ) cos(θ ) ≠ 0
4.13
− r (θ ) sin(θ ) + r '(θ ) cos(θ )
r (θ ) cos(θ ) + r '(θ ) sin(θ )
se r (θ ) cos(θ ) + r '(θ ) sin(θ ) ≠ 0
4.14
φ (θ ) = arctan
ψ (θ ) = arctan
E’ utile osservare che:
φ '(θ ) =
r (θ ) 2 + 2r '(θ ) 2 − r (θ ) r ''(θ )
r (θ ) 2 + r '(θ ) 2
4.15
da cui si deduce:
> 0
φ '(θ )
< 0
se r (θ ) 2 + 2r '(θ ) 2 − r (θ ) r ''(θ ) > 0
4.16
se r (θ ) 2 + 2r '(θ ) 2 − r (θ ) r ''(θ ) < 0
La 4.16 consente di rappresentare esplicitamente il versore normale interno û .
4.5 Versore normale interno
Il versore normale interno û a γ in un suo punto qualsiasi P = (θ , r (θ )) è la funzione vettoriale così
definita per θ ∈ [ θ a , θb ] :
r (θ ) cos(θ ) + r '(θ ) sin(θ ) ˆ − r (θ ) sin(θ ) + r '(θ ) cos(θ ) ˆ
uˆ (θ ) =
−
i+
j
r (θ ) 2 + r '(θ ) 2
r (θ ) 2 + r '(θ ) 2
4.17
Osservazione 4.1 I versori tˆ, nˆ , uˆ in termini dei versori eˆ r , eˆ θ
Per rappresentare tˆ, nˆ , uˆ in termini dei versori eˆ r , eˆ θ basta sostituire nelle 4.8, 4.9 e 4.17 i versori
ˆi , ˆj con le loro espressioni in termini dei versori eˆ , eˆ . Come si deduce immediatamente dalla Fir
θ
gura 4.2, si ha:
ˆi cos(θ ) eˆ − sin(θ )eˆ
=
r
θ
4.18
ˆj sin(θ ) eˆ + cos(θ ) eˆ
=
r
θ
4.19
14
Figura 4.2
Procedendo come indicato, si trova che:
=
tˆ(θ )
r '(θ )
r (θ ) 2 + r '(θ ) 2
nˆ (θ ) = ±
eˆ r +
r (θ )
r (θ ) 2 + r '(θ ) 2
eˆ r
r (θ )
uˆ (θ ) =
−
eˆ r +
r (θ ) 2 + r '(θ ) 2
r (θ )
r (θ ) 2 + r '(θ ) 2
eˆθ
r '(θ )
r (θ ) 2 + r '(θ ) 2
r '(θ )
r (θ ) 2 + r '(θ ) 2
4.20
eˆθ
4.21
eˆθ
4.22
Nella 4.21, i segni superiori si devono usare se r (θ ) 2 + 2r '(θ ) 2 − r (θ ) r ''(θ ) < 0 , mentre i segni inferiori si devono usare se r (θ ) 2 + 2r '(θ ) 2 − r (θ ) r ''(θ ) > 0 .
Osservazione 4.2 Rappresentazione in forma polare di una curva espressa in forma parametrica
Sia γ una curva piana che in un sistema di coordinate cartesiane ortogonali {0, x, y} fissato nel suo
piano risulti rappresentata dalle seguenti equazioni parametriche:
x = x(t )
y = y (t )
4.23
dove si suppone t ∈ [ ta , tb ] ed x(t ), y (t ) due assegnate funzioni di classe C n [ ta , tb ], n ≥ 2 . Allora,
se la curva γ ammette la rappresentazione in forma polare:
r = r (θ )
4.24
con θ ∈ [ θ a , θb ] ed r (θ ) di classe C n [ θ a , θb ], n ≥ 2 , questa, nel sistema di coordinate {0, x, y} si
ottiene eliminando t dalle seguenti relazioni:
15
=
r
x(t ) 2 + y (t ) 2
4.25
y (t )
x(t )
4.26
θ = arctan
Ricordiamo che non tutte le curve piane γ rappresentabili nella forma 4.23 ammettono rappresentazione polare. Non la ammettono ad esempio le rette passanti per l’origine, oppure le curve per le quali
r (θ ) risulterebbe a più valori (e quindi non una funzione).
16
5. DETERMINAZIONE DELLE PROPRIETA’ GEOMETRICHE INTRINSECHE DELLE
CURVE PIANE NEL CASO DI CURVE RAPPRESENTATE IN FORMA CARTESIANA
IMPLICITA
Sia γ una curva piana regolare almeno del secondo ordine che rispetto ad un arbitrario sistema di
coordinate cartesiane ortogonali {0, x, y} fissato nel suo piano, risulti rappresentata in forma cartesiana implicita, cioè per mezzo dell’equazione:
F ( x, y ) = 0
5.1
La situazione considerata è schematicamente mostrata in Figura 5.1, in cui è riportata la curva definita
) x3 − y 2 .
implicitamente dalla funzione F ( x, y=
Figura 5.1
Quando una curva γ è rappresentata in forma cartesiana implicita, la situazione è più complessa che
nei casi trattati nei precedenti paragrafi in quanto un’equazione del tipo 5.1 può definire γ come
unione di più curve γ k , rappresentabili in forma cartesiana esplicita y = f k ( x) , ciascuna delle quali
costituisce un cosiddetto ramo di γ . Ne segue possono esistere in γ dei punti di diramazione per il
versore t̂ ed il versore û può non essere orientato verso un’unica parte di piano. Chiaramente, per
ogni punto di γ , il versore n̂ sarà orientato verso la parte di piano in cui γ presenta la concavità e la
coppia ordinata di versori ( t̂ , û ) risulterà sinistrogira. Ad esempio, nel caso riportato in Figura 5.1
la curva γ è costituita da due rami: γ 1 di equazione y = x3 e γ 2 di equazione y = − x3 , il punto
P0 = (0, 0) è un punto di diramazione per t̂ ed il versore û presenta la particolarità sopra citata.
Quanto ora detto è mostrato in Figura 5.2 e Figura 5.3.
Figura 5.2
Figura 5.3
17
Per determinare le proprietà geometriche intrinseche di una curva γ rappresentata in forma cartesiana
implicita, si possono utilizzare due approcci. Uno basato sull’utilizzo del teorema di Dini per le funzioni implicite ed uno basato sull’utilizzo delle proprietà del gradiente del campo scalare F ( x, y ) .
5.1 Utilizzo del teorema di Dini
Come è noto, se per tutti i punti P = ( x, y ) di un intorno del punto P0 = ( x0 , y0 ) di γ , l’equazione 5.1
definisce y implicitamente come funzione differenziabile di x, se cioè per ogni x appartenente ad un
intorno I x0 di x0 si può scrivere:
y = f ( x)
5.2
dove f ( x) è tale che F [ x, f ( x)] ≡ 0 ∀x ∈ I x0 , allora la derivata di f ( x) in x0 ha il valore numerico
fornito dalla seguente relazione:
f '( x0 ) = −
∂F ( x, y )
x = x0
∂x
y = y0
5.3
∂F ( x, y )
x = x0
∂y
y = y0
Chiaramente, la funzione f ( x) soddisfa alla condizione f ( x0 ) = y0 . Tuttavia, la funzione f ( x) non
si conosce (si sa solo che esiste). Operativamente quindi, scelto un punto P di γ avente ascissa x0 , il
valore y0 = f ( x0 ) si deve ottenere risolvendo (eventualmente con tecniche numeriche) l’equazione
F ( x0 , y ) = 0 nell’intorno del punto P. Si tenga presente infatti che l’equazione F ( x0 , y ) = 0 può ammettere più di una soluzione e quindi occorre riferirsi ad un fissato punto di γ .
Partendo dalla 5.3 si può poi calcolare il valore della derivata seconda di f ( x) in x0 . Infatti la 5.3
può essere riscritta nella seguente forma equivalente:
f '( x0 ) =
−
∂F ( x, y )
x = x0
∂x
y = f ( x0 )
5.4
∂F ( x, y )
x = x0
∂y
y = f ( x0 )
e considerando x0 come variabile, derivando la 5.4 rispetto ad x0 , si ottiene:
f ''( x0 ) =
∂F ( x, y )
x = x0
x
∂
y = f ( x0 )
d
−
dx0 ∂F ( x, y )
x = x0
∂y
y = f ( x0 )
5.5
Eseguendo i calcolo a secondo membro della 5.5, il cui termine fra parentesi è una funzione composta
del tipo G [ x0 , f ( x0 )] , e sostituendo alle derivate f '( x0 ) che in tal modo vengono generate la loro
18
espressione fornita dalla 5.4, si perviene ad un’espressione di f ''( x0 ) in cui compaiono x0 ed f ( x0 ),
cioè valori noti.
La possibilità di calcolare per ogni punto fissato P0 = ( x0 , y0 ) di γ i valori di f '( x0 ) ed f ''( x0 ) della
funzione f ( x) che definisce in un intorno di P0 una rappresentazione cartesiana esplicita di γ , permette, in linea di principio, di determinare tutte le proprietà geometriche intrinseche della curva γ
relative al punto P0 , tramite le formule riportate nel Paragrafo 3. Chiaramente, così facendo le proprietà geometriche intrinseche di γ sono l’unione delle proprietà geometriche intrinseche dei vari
rami γ k che costituiscono γ , ciascuno rappresentato da un’equazione del tipo y = f k ( x) con f k ( x)
definita implicitamente dall’equazione F ( x, y ) = 0 per tutti i valori di x ascissa dei punti di γ k . E’
tuttavia da osservare, che mentre la determinazione dei versori tˆ, nˆ ed û come quella degli scalari
κ , ρ , φ e ψ è sempre possibile per ogni punto P0 di γ del quale si conoscono le coordinate, il
calcolo dell’elemento di lunghezza d’arco ds risulta impossibile se non si conosce esplicitamente la
funzione f k ( x) che individua in forma cartesiana esplicita il ramo γ k di γ del quale si intende determinare il ds .
5.2 Utilizzo delle proprietà del gradiente del campo scalare F(x, y)
Utilizzando le proprietà del gradiente del campo scalare F ( x, y ) , si può dimostrare che posto per
ogni punto P = ( x, y ) di γ (e quindi tale F (P) = 0 , per cui x e y non possono considerarsi assumere
variabili indipendenti):
gˆ (P) =
∇F (P)
| ∇F (P) |
k (P) = ∇ ⋅ gˆ (P)
;
;
ξ (P) =
< gˆ (P) | ˆi >
< gˆ (P) | ˆj >
5.6
dove ∇ è l’operatore nabla:
=
∇
∂ ˆ ∂ ˆ
i+
j
∂x
∂y
5.7
e con < gˆ (P) | ˆi > e < gˆ (P) | ˆj > si è rispettivamente indicato il prodotto scalare fra gˆ (P) ed i versori
î e ĵ , le proprietà geometriche intrinseche di γ risultano esprimibili per mezzo dalle formule qui di
seguito riportate.
▪ Lunghezza dell’arco (relativo al ramo γ k di γ , rappresentato dall’equazione y = f k ( x) )
ds
=
1 + ξ [ x, f k ( x)]2 dx
ovvero
ds
=
1 + f k ( x) 2 dx
5.8
▪ Versore tangente e versore normale
=
tˆ(P)
1
1 + ξ (P)
2
ˆi −
ξ (P)
1 + ξ (P)
2
ˆj
5.9
nˆ (P) = − sgn[k (P)] gˆ (P)
5.10
19
▪ Curvatura e raggio di curvatura
κ (P) = k (P)
;
ρ (P) =
1
k (P)
5.11
▪ Pendenza e copendenza
1
2
1 + ξ (P)
−ξ (P)
φ (P) = arccos
1 + ξ (P) 2
ψ (P) = arccos
oppure
φ (P) = − arctan (ξ (P) )
oppure
ψ (P) = − arctan
5.12
1
ξ (P)
5.13
▪ Versore normale interno
uˆ (P) = − sgn[φ (P)]sgn[k (P)] gˆ (P)
5.14
Osservazione 5.1 Forma esplicita di gˆ (P) , k (P) e ξ (P)
Dalle 5.6 si ottiene esplicitamente:
∂F (P)
∂x
gˆ (P)
k (P)
2
∂F (P) ∂F (P)
+
∂x ∂ y
2
ˆi +
∂F (P)
∂
∂x
2
∂x ∂F (P) ∂F (P) 2
+
∂
x
∂y
∂F (P)
∂y
2
∂F (P) ∂F (P)
+
∂x ∂ y
2
ˆj
∂F (P)
∂
∂y
+
2
2
∂y ∂F (P) ∂F (P)
+
∂
x
∂y
∂F (P) ∂F (P)
∂x ∂ y
ξ (P) =
5.15
5.16
5.17
Si noti che confrontando la 5.17 con la 5.3 risulta che ξ (P) = − f '( x0 ).
Osservazione 5.2 Segno reale dei termini calcolati
Come si è detto, nelle precedenti relazioni il punto P = ( x, y ) si suppone appartenente a γ e quindi
tale che F (P) = 0 . I valori di x e y che compaiono nelle precedenti relazioni non si possono quindi
20
considerare indipendenti. Ne segue che il valore delle componenti di tˆ, nˆ ed û e quello degli scalari
κ , ρ , φ e ψ in un fissato punto di γ vanno calcolati considerando che:
∂F (P) ∂F ( x, y )
=
∂x
∂x
;
y = fk ( x )
∂F (P) ∂F ( x, y )
=
∂y
∂y
5.18
y = fk ( x )
Così ad esempio, per la curva γ rappresentata dall’equazione x3 − y 2 =
0 , la seconda delle 5.6 fornisce:
k (P) = −
2 x( x3 − 4 y 2 )
(x
4
+ 4 y2 )
5.19
3/2
Ma questo non è un campo scalare positivo se 2 x( x 3 − 4 y 2 ) > 0 , infatti x e y devono soddisfare alla
0 . Si vede così che risulta k (P) > 0 ∀P ∈ γ − {(0, 0)} . Infatti, dalla 5.18 si ottiene
condizione x3 − y 2 =
y 2 = x3 e quindi la 5.19 fornisce in pratica ∀P ∈ γ − {(0, 0)} :
k (P) =
2 3 x4
( 3x 4 + 4 x3 )
3/2
⇒
k (P) > 0
∀P ∈ γ − {(0, 0)}
5.20
In conclusione del paragrafo mostriamo un esempio di calcolo dei versori tˆ, nˆ ed û e degli scalari
κ e φ in un punto di una curva rappresentata in forma cartesiana implicita F ( x, y ) = 0 .
Esempio 5.1
Sia γ la curva rappresentata implicitamente dalla funzione:
x 4 − 3x 2 y + y 3 − 2 =
0
5.21
In Figura 5.4 è mostrata la parte di γ relativa al rettangolo [−5, 5] × [−5, 5] . Fissato su γ punto P0
di coordinate x0 = 1 , y0 =1.87939 (il valore di y0 è stato ottenuto numericamente risolvendo fa 5.21
con x = 1 , cioè l’equazione y 3 − 3 y − 1 =0 ), calcoliamo in tale punto, con i due approcci studiati, i
versori tˆ, nˆ ed û e degli scalari κ e φ .
Figura 5.4
21
Nel caso in esame si ha:
F ( x, y ) = x 4 − 3 x 2 y + y 3 − 2
5.22
per cui risulta:
∂F ( x, y )
= 4 x3 − 6 x y
∂x
∂F ( x, y )
=
−3 x 2 + 3 y 2
∂y
;
5.23
A) Utilizzo del teorema di Dini
Dalla 5.4 si ottiene:
f '( x) =
4 x3 − 6 x f ( x)
3 x 2 − 3 f ( x) 2
5.24
dove con f ( x) si è indicata la funzione che permette di rappresentare γ in un intorno di P0 nella
forma y = f ( x) . La derivata seconda di f ( x) si ottiene poi dalla formula:
f ''( x) =
d 4 x3 − 6 x f ( x)
dx 3 x 2 − 3 f ( x) 2
5.25
A calcoli fatti, per il punto P0 considerato, risulta:
f (1) = 1.87939
f '(1) = 0.95788
;
f ''(1) = 0.055879
;
5.26
Possiamo quindi concludere in base alle 3.8 e 3.9 (quest’ultima scritta con i segni corrispondenti a
f ''( x) > 0 ), che:
tˆ( x0 , y0 ) =
1
1 + f '( x0 )
2
ˆi +
f '( x0 )
1 + f '( x0 )
2
ˆj =
1
1 + (0.95788)
2
ˆi +
0.95788
1 + (0.95788)
2
ˆj =
=
tˆ( x0 , y0 ) 0.722152 ˆi + 0.691735 ˆj
f '( x0 )
ˆi +
−
nˆ ( x0 , y0 ) =
2
1 + f '( x0 )
5.27
1
0.95788
ˆj =
ˆi +
−
2
1 + f '( x0 )
1 + (0.95788)
2
1
1 + (0.95788)
2
ˆj =
− 0.691735 ˆi + 0.722152 ˆj
tˆ( x0 , y0 ) =
5.28
I valori di κ ( x0 , y0 ) e φ ( x0 , y0 ) si ottengono invece rispettivamente dalla 3.10 e 3.11. Si ha:
=
κ ( x0 , y0 )
f ''( x0 )
=
3/2
( 1 + f '( x0 )2 )
0.055879
=
0.021044
2 3/2
+
1
(0.95788)
(
)
=
φ=
( x0 , y0 ) arctan (=
f '( x0 ) ) arctan ( 0.95788
) 43.76782°
22
5.29
5.30
Infine, dalla 3.14 si ottiene:
− 0.691735 ˆi + 0.722152 ˆj
uˆ ( x0 , y0 ) =
5.31
Dunque uˆ ( x0 , y0 ) = nˆ ( x0 , y0 ) , come si poteva già capire essendo f ''(1) > 0 e quindi φ '(1) > 0 .
B) Utilizzo delle proprietà del gradiente di F(x, y)
Utilizzando le 5.23, dalle 5.15 – 5.17 si ottiene per il punto P0 considerato:
gˆ ( x0 , y0 ) =
− 0.691735 ˆi + 0.722152 ˆj
5.32
k ( x0 , y0 ) = −0.021044
5.33
ξ (P) = −0.95788
5.34
Usando questi valori nelle 5.9 – 5.14 si ritrovano i risultati ottenuti in precedenza.
_____________________________
23
APPENDICE A.1 Cinematica piana di un punto materiale
Consideriamo un punto materiale che percorre una traiettoria piana γ , che rispetto ad un sistema di
coordinate cartesiane ortogonali {0, x, y } fissato nel suo piano, è rappresentata dalla funzione:
=
r (t ) x(t ) ˆi + y (t ) ˆj
A1.1
Allora, come è noto, la velocità istantanea v (t ) e l’accelerazione istantanea a(t ) del punto materiale
sono in ogni istante definite dalle relazioni (purché le derivate esistano):
v (t ) = r (t )
A1.2
a(t ) = r(t )
A1.3
Supponendo x(t ) ed y (t ) regolari almeno del secondo ordine, indichiamo con s = s (t ) la legge oraria
del moto. Per definizione ds = s (t + dt ) − s (t ) è l’elemento di lunghezza di γ come definito dalla 1.2.
Dunque, supponendo s (0) = 0 :
t
⌠
=
s (t ) x (t ) 2 + y (t ) 2 dt
⌡
A1.4
0
Siano quindi t̂ ed n̂ il versore tangente ed il versore normale principale a γ , così come definiti dalle
1.5. Allora, la velocità istantanea v (t ) e l’accelerazione istantanea a(t ) del punto materiale si possono in ogni istante esprimere oltre che nella forma A1.2 – A1.3, anche nella forma seguente:
v (t ) = v(t ) tˆ
A1.5
v(t ) 2
=
a(t ) a (t ) tˆ +
nˆ
ρ (t )
A1.6
dove v(t ) è la velocità scalare istantanea, a (t ) è l’accelerazione scalare istantanea e ρ (t ) è il raggio
di curvatura istantaneo della traiettoria. Per definizione:
v(t ) = s(t )
Inoltre
v(t ) = | v (t ) |
A1.7
a (t ) =
s (t )
A1.8
Si ha poi:
=
| a(t ) |
1
ρ (t )
ρ (t ) 2 a(t ) 2 + v(t ) 4
A1.9
Il raggio di curvatura istantaneo ρ (t ) si può ottenere tramite la A1.5 purché siano noti v(t ) , dalla cui
conoscenza si può ottenere a (t ) , ed | a(t ) | . Un’altra formula per calcolare ρ (t ) è la seguente (che
segue dalla 2.6 in forza delle A1.2 ed A1.3):
24
ρ (t ) =
| v (t ) | 3
a(t ) ∧ v (t )
ρ (t ) =
⇒
| v (t ) | 2
a(t ) |sin[ β (t)]
A1.10
dove con β (t ) si è indicato l’angolo istantaneo formato dai vettori v (t ) ed a(t ) . Si ha:
< v (t ) | a(t ) >
| v (t ) | | a(t ) |
β (t ) = arccos
A1.11
dove con < v (t ) | a(t ) > si è indicato il prodotto scalare fra v (t ) ed a(t ) . Si noti che se v (t ) ed a(t )
si esprimono tramite le A1.5 ed A1.6, la prima delle A1.10 si riduce ad un’identità e quindi non è
utile per il calcolo di ρ (t ) .
Osservazione A1.1 Direzione e verso della velocità e della accelerazione istantanea
Dalla A1.5 segue che v (t ) è costantemente tangente alla traiettoria ed orientata nel senso del moto.
Dalla A1.6 segue invece che a(t ) ha sempre una componente rivolta verso il centro di curvatura
istantaneo (la componente di versore n̂ ). Il segno di a (t ) dipende invece dal fatto che il punto materiale acceleri ( a (t ) > 0 ) si muova con velocità di modulo costante ( a (t ) = 0 ) oppure deceleri
(a (t ) < 0) .
Osservazione A1.2 Moto in coordinate polari
Se la traiettoria γ , supposta regolare almeno del secondo ordine, è rappresentata rispetto ad un sistema di coordinate polari polare {O, r , θ } , per cui il moto del punto materiale sia descritto dalle
equazioni:
r = r (t )
θ = θ (t )
A1.12
allora, la velocità istantanea v (t ) e l’accelerazione istantanea a(t ) del punto materiale risultano
espresse in ogni istante dalle seguenti relazioni:
=
v (t ) r(t ) eˆ r + r (t )θ(t ) eˆ θ
A1.13
[
a(t ) =−
r (t ) r (t )θ(t ) 2 ] eˆ r + [2r(t )θ(t ) + r (t )θ(t )] eˆ θ
A1.14
dove con eˆ r , eˆ θ si sono indicati i versori base del sistema di coordinate {O, r , θ } .
Si noti che esplicitando (se possibile) t dalla seconda delle A1.12 e successivamente esprimendo nella
prima delle A1.12 r nella forma r = r (θ ) , si ottiene l’equazione della traiettoria in forma polare. Si
noti anche che fissato un sistema di coordinate cartesiane ortogonali {0, x, y } con origine ed asse x
coincidenti rispettivamente con l’erigine e l’asse polare del sistema {O, r , θ } , l’equazione cartesiana
della traiettoria risulta la seguente:
=
r (t ) r (t ) cos[θ (t )] ˆi + r (t ) sin[θ (t )] ˆj
A1.15
____________________________
25
BIBLIOGRAFIA
[1] T. M. Apostol, “Calcolo, Volume 3 – Analisi 2”, Edizioni Boringhieri.
[2] M. M. Lipschutz, “Geometria Differenziale”, Collana SCHAUM n. 64, Edizioni ETAS Libri.
[3] M. Bruno, M. D’Agostino, M. L. Fiandri, “Esercizi di Fisica 1”, Edizioni CLUEB.
26
INDICE
1. LE PROPRIETA’ GEOMETRICHE INTRINSECHE DELLE CURVE PIANE
1
2. FORMA ESPLICITA DELLE PROPRIETA’ GEOMETRICHE INTRINSECHE
DELLE CURVE PIANE NEL CASO DI CURVE RAPPRESENTATE IN FORMA
PARAMETRICA
7
3. FORMA ESPLICITA DELLE PROPRIETA’ GEOMETRICHE INTRINSECHE
DELLE CURVE PIANE NEL CASO DI CURVE RAPPRESENTATE IN FORMA
CARTESIANA ESPLICITA
9
4. FORMA ESPLICITA DELLE PROPRIETA’ GEOMETRICHE INTRINSECHE
DELLE CURVE PIANE NEL CASO DI CURVE RAPPRESENTATE IN FORMA
POLARE
12
5. DETERMINAZIONE DELLE PROPRIETA’ GEOMETRICHE INTRINSECHE
DELLE CURVE PIANE NEL CASO DI CURVE RAPPRESENTATE IN FORMA
CARTESIANA IMPLICITA
17
APPENDICE A.1 Cinematica piana di un punto materiale
24
BIBLIOGRAFIA
26
27