Presentazione di PowerPoint

Formazione e pratica educativa della
METROLOGIA
Riferimento Protocollo d’intesa USR-INRiM-CE.SE.DI-IGMEE
(siglato il 28 ottobre 2010, rinnovato nel febbraio 2013)
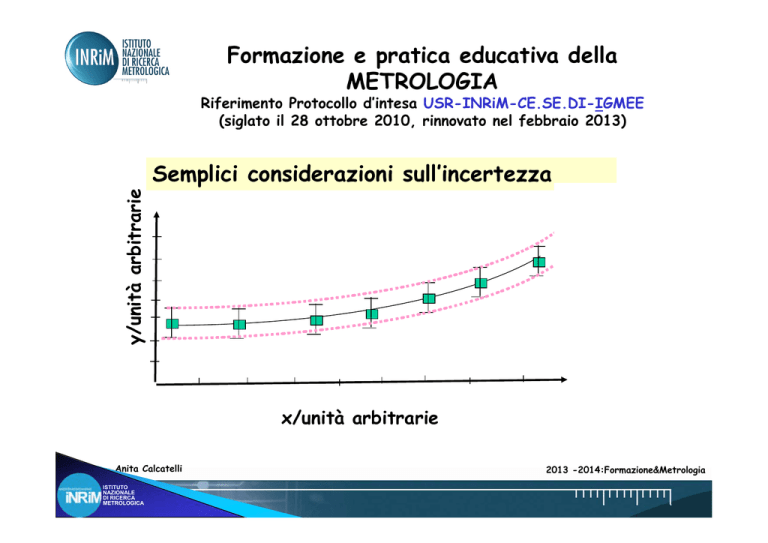
y/unità arbitrarie
Semplici considerazioni sull’incertezza
x/unità arbitrarie
Anita Calcatelli
ISTITUTO
NAZIONALE
DI RICERCA
METROLOGICA
2013 -2014:Formazione&Metrologia
Incertezza
• Considerazioni preliminari
• Il linguaggio
• Incertezza: concetti di base ed
esempi
I primi due punti sono essenzialmente il
riepilogo di concetti già visti nei
precedenti moduli, e sono indispensabili
per procedere nel capitolo sull’incertezza.
Anita Calcatelli
ISTITUTO
NAZIONALE
DI RICERCA
METROLOGICA
2013 -2014:Formazione&Metrologia
L'INCERTEZZA DI MISURA
La parola “incertezza” significa dubbio
circa la validità dei risultati di una
misurazione.
Si eseguono e producono misure per prendere,
sulla base del risultato ottenuto, delle
decisioni come per esempio se bloccare il
traffico in funzione di misure di livello di
inquinamento massimo ammesso, accettare un
pezzo su cui si sia stabilito il livello di
“tolleranza”, assumere o meno un medicinale
in base ai risultati di esami clinici.
Anita Calcatelli
ISTITUTO
NAZIONALE
DI RICERCA
METROLOGICA
2013 -2014:Formazione&Metrologia
Si decide se immettere in commercio un
prodotto secondo il risultato della
misurazione di alcune sue caratteristiche,
garantite dal produttore e controllate da
chi di dovere.
La necessità di decidere
problemi alle misure.
pone
seri
E ladomanda fondamentale è
quale ruolo gioca nella decisione l'incertezza che
sempre è associata ad ogni azione sperimentale?
lo vedremo piano piano strada facendo
Anita Calcatelli
2013 -2014:Formazione&Metrologia
L'incertezza nelle misure è oggi ben più
di un concetto; la stima del suo valore si
basa su una procedura di calcolo
codificata in una norma internazionale.
ISO/GUM: Evaluation of measurement data — Guide
to the expression of uncertainty in measurement,
JCGM 100:2008 ;GUM 1995 with minor corrections
(http://www.bipm.org/en/publications/guides/, o
anche http./www.oiml.org/publications/?publi=3&pu)
Norma italiana: “guida all’espressione dell’incertezza
di misura”, UNI CEI ENV 13005, luglio 2000
Anita Calcatelli
2013 -2014:Formazione&Metrologia
La nostra cultura fa fatica ad accettare
la coesistenza dell'incertezza con la
necessità di decidere senza possibilità di
dubbi, senza esitazioni.
C’é una nuova branca della metrologia:
quella
che
si
occupa
delle
regole
decisionali, ossia di come decidere
minimizzando i rischi d'errore.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Un presupposto indispensabile ad ogni
discorso sulle regole decisionali è la
riferibilità delle misure, ossia l'esistenza
di una catena ininterrotta di confronti
che consenta il loro collegamento a
campioni riconosciuti.
La necessità di decidere ci riporta così
alle reti di laboratori, agli accordi di
mutuo riconoscimento delle misure che
essi producono, in un costante tentativo
di estendere la riferibilità a tutte le
misure prodotte nel mondo.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Dalla guida all’espressione dell’incertezza
UNI CEI ENV 13005
Benché questa guida fornisca uno schema generale
per valutare l’incertezza, essa non può sostituirsi al
pensiero critico, all’onestà intellettuale ed alla
capacità professionale.
La valutazione dell’incertezza non è né un compito di
routine né un esercizio puramente matematico, ma
dipende dalla conoscenza approfondita della natura
del misurando e della misurazione.
La qualità e l’utilità dell’incertezza attribuita al
risultato di una misurazione dipendono, in definitiva,
dall’approfondimento, dall’analisi critica e
dall’integrità morale di chi contribuisce ad
assegnarne
il valore.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Il linguaggio
Alcuni concetti di base liberamente tratti da
Vocabolario Internazionale di Metrologia
[Concetti di base e generali e termini associati
(VIM)]
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Grandezza
Attributo di un fenomeno, corpo o
sostanza, che può essere distinto
qualitativamente
o
determinato
quantitativamente, massa, forza,
energia, corrente ….
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Varie grandezze
Grandezza di base (fondamentale): grandezza
che, in un sistema di grandezze, è
convenzionalmente
accettata
come
indipendente dalle altre
lunghezza,
massa,
intervallo di tempo,
temperatura termodinamica,
intensità di corrente elettrica,
intensità luminosa,
Anita Calcatelli
quantità di sostanza.
2013 -2014:Formazione&Metrologia
Grandezza derivata: grandezza che, in un
sistema di grandezze, è definita in funzione
delle grandezze di base di quel sistema.
superficie di un rettangolo = lato1 x lato2
volume di un parallelepipedo= lato1x lato2x lato3
velocità = spazio/intervallo di tempo
accelerazione = velocità/intervallo di tempo=
spazio/tempo 2
forza = massa x accelerazione =
massa x spazio/tempo2
pressione =forza/superficie=
2
[massaxspazio/tempo2]/spazio
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Grandezza di influenza: grandezza che non è
oggetto della misurazione, ma che influisce sul
valore del misurando o sulle indicazioni degli
strumenti di misura
Esempio: se una barra d’acciaio deve essere
misurata a  1 m, pressione e temperatura
dovranno essere specificate: si dovrà dare la
lunghezza della barra, per es, a 25 °C e 105 Pa.
Ciò non è necessario se la lunghezza della barra
deve essere fornita a  1 mm.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Esempio: la temperatura nella misurazione di
pressione e di molte altre grandezze
p
 M g (1  
i
i
l
a
/  m )  C

A0 (1  p ) 1  ( p   c )(t  t rif )

cioè forza peso che agisce sull’unità di superficie
Pressione di
riferimento
Pressione
incognita
p=f(Mi, gL, A0, t)
p=HggLh Hg=f(t) attraverso il
coefficiente di dilatazione termica
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Unità di
misura: grandezza determinata,
adottata
per
convenzione,
usata
per
esprimere quantitativamente grandezze aventi
la stessa dimensione (riferimento Norma UNI
4546)
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Simbolo di una unità di misura: segno
convenzionale che designa una unità di misura
Sistema di unità di misura: insieme stabilito di
unità per un determinato sistema di grandezze
(ad esempio il SI, Sistema Internazionale di
unità di misura)
SI costituito da
unità di base
e
unità derivate
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Unità di base
grandezza
lunghezza
massa
unità
metro
kilogrammo
simbolo
definizione
m
tragitto percorso dalla luce nel vuoto
in un intervallo tempo pari a 1/299
792 458 di secondo
kg
massa del campione del platino-iridio,
conservato presso il Bureau
Internazional des Poids et Mesures di
Sèvres (Parigi)
5?
1
0
2
intervallo di secondo
tempo
s
durata pari a 9 192 631 770 periodi
della radiazione corrispondente alla
transizione tra i livelli iperfini dello
stato fondamentale dell'atomo di
cesio-133
Destinate a cambiare
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Grandezza
intensità di
corrente
elettrica
unità
ampere
Temperatura kelvin
termodinami
ca
simbolo
A
definizione
quantità di corrente che scorre
all'interno di due fili paralleli e
rettilinei, di lunghezza infinita e
sezione trascurabile, immersi nel
vuoto ad una distanza di un metro,
induce in loro una forza di attrazione
o repulsione di 2*10-7 N per ogni
metro di lunghezza
?
5
1 valore
20
K
corrispondente a 1/273,16
della temperatura termodinamica del
punto triplo dell'acqua
Destinate a cambiare
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Grandezza
quantità di
sostanza
unità
simbolo
mole
mol
?
5
1
20
intensità
luminosa
candela
cd
definizione
quantità di materia di una
sostanza tale da contenere tante
particelle elementari quante ne
contengono 0,012 kg di carbonio12. Tale valore corrisponde al
numero di Avogadro
intensità luminosa di una sorgente
che emette una radiazione
monocromatica con frequenza
5,4*10-14 Hz e intensità
energetica di 1/683 W/sr.
Destinate a cambiare
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Sulla possibile revisione del SI, proposta per
CGPM 17-21 ottobre 2011
È intenzione del CIPM proporre la revisione del SI come segue:
Il SI sarà un sistema in cui:
•La frequenza della transizione tra due livelli iperfini dello stato fondamentale
dell’atomo di cesio 133 (133Ce)hfs è esattamente 9 192 631 770
hertzsecondo
•La velocità della luce nel vuoto è esattamente 299 792 458 metri al
secondometro
•La costante di Planck è esattamente 6,626 06X joule al secondokilogrammo
•La carica elementare e è esattamente 1,602 17X coulombampere
•La costante di Boltzman è esattamente 1.380 6X joule per kelvinkelvin
•La costante di Avogadro é esattamente 6.022 14X reciproco della molemole
•L’efficienza luminosa Kcd di una radiazione monocromatica di frequenza
540x 1012 Hz è esattamente 683 lumen per wattcandela
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Il SI continuerebbe ad essere costituito dalle
sette unità fondamentali
Esempio di possibile ridefinizione
Il secondo, simbolo s, è l’unità di tempo, il
suo valore è stabilito fissando il valore
numerico della frequenza corrispondente alla
transizione tra i due livelli iperfini dello stato
fondamentale dell'atomo di cesio 133, a riposo
e a temperatura di 0 K, esattamente eguale
a 9 192 631 770 quando è espresso in unità
SI s-1 che è eguale a Hz
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Unità derivate
Le unità SI derivate si ottengono combinando tra
loro le unità di base in monomi del tipo seguente:
m· kg · s · A· K · mol · cd
con coeff. num. 1; gli esponenti   , ecc, sono
numeri interi (zero incluso).
F = massa x accelerazione = kg m/s2 = newton N
p = F/S = N/m2 =pascal  Pa
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Multipli delle unità di misura: unità di misura più
grande ottenuta da una determinata unità secondo
convenzioni di scala (uno dei multipli decimali del metro
è il kilometro; uno dei multipli non decimali del secondo
è l’ora)
Sottomultipli di una unità: unità di misura più
piccola ottenuta da una determinata unità secondo
convenzioni di scala (uno dei sottomultipli decimali
del metro é il millimetro)
Anita Calcatelli
2013 -2014:Formazione&Metrologia
multipli e sottomultipli
10
24
yotta
Y
1 000 000 000 000 000 000 000 000
10
21
zetta
Z
1 000 000 000 000 000 000 000
10
18
exa
E
1 000 000 000 000 000 000
10
15
peta
P
1 000 000 000 000 000
10
12
tera
T
1 000 000 000 000
10
9
giga
G
1 000 000 000
10
6
mega
M
1 000 000
10
3
chilo
k
1 000
10
2
etto
h
100
10
1
deca
da
10
10
-1
dieci
d
0.1
10
-2
centi
c
0.01
10
-3
milli
m
0.001
10
-6
micro
µ
0.000 001
10
-9
nano
n
0.000 000 001
10
-12
pico
p
0.000 000 000 001
10
-15
femto
f
0.000 000 000 000 001
10
-18
atto
a
0.000 000 000 000 000 001
10
-21
zepto
z
0.000 000 000 000 000 000 001
10
-24
yocto
y
0.000 000 000 000 000 000 000 001
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Campione
campione materiale, strumento per misurazione
o sistema di misurazione inteso a definire,
realizzare, conservare o riprodurre una unità
ovvero uno o più valori noti di una grandezza
per trasmetterli per confronto ad altri
strumenti di misurazione.
esempi: massa campione di 1 kg, blocchetto
di riscontro campione, resistore campione da
100 , amperometro campione, campione
atomico di frequenza al cesio:
Anita Calcatelli
Istituto e Museo di storia della
Scienza-Firenze
2013 -2014:Formazione&Metrologia
Vari campioni
campione primario: campione che presenta le migliori
caratteristiche metrologiche in un certo dominio
specificato
campione secondario: campione il cui valore è fissato
per confronto con il campione primario
campione internazionale: campione riconosciuto da un
accordo
internazionale
per
servire
come
base
internazionale a fissare il valore di tutti gli altri
campioni della grandezza considerata
Anita Calcatelli
2013 -2014:Formazione&Metrologia
campione nazionale: campione
riconosciuto
con
decisione
ufficiale nazionale come base
per fissare, in una nazione, il
valore di tutti gli altri campioni
della grandezza considerata (il
campione nazionale di un paese
è sovente un campione primario)
campione di riferimento: campione, in genere della
migliore qualità metrologica disponibile in un dato
luogo, dal quale sono derivate le misurazioni eseguite in
quel luogo, per es. in un reparto di produzione (calibro
tarato).
Anita Calcatelli
2013 -2014:Formazione&Metrologia
campione di lavoro: campione, generalmente tarato
rispetto ad un campione di riferimento, che è usato
comunemente per tarare o controllare campioni
materiali o strumenti per misurazione.
campione di trasferimento: campione usato come
intermediario per confrontare tra loro campioni,
campioni materiali o strumenti di misurazione.
campione viaggiante: campione talvolta appositamente
realizzato destinato ad essere trasportato in luoghi
differenti (ad esempio campione atomico di frequenza
al cesio, portatile, alimentato a batteria)
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Metrologia: campo della conoscenza
riguarda le misurazioni.
che
Possiamo considerare la metrologia come un linguaggio
internazionale, il solo linguaggio internazionale, che
sottende un grosso lavoro di ricerca di sempre
migliori definizioni delle unità, di ottimizzazione dei
campioni, di valutazione degli intervalli entro cui il
valore fornito di una grandezza può ragionevolmente
variare.
La metrologia mette già in atto un’ampia
collaborazione internazionale come forse non si
realizza in altri campi per i quali può costituire un
esempio da seguire per trovare regole e modelli
(campioni) condivisi in un’ampia visione di riferibilità
globale.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Misurando: grandezza oggetto della misurazione,
ad esempio la lunghezza del diametro di una sfera
o la massa di un corpo.
Misurazione: insieme di operazioni che ha lo scopo di
attribuire un valore numerico di una grandezza.
Si confronta l'unità di misura di una determinata
grandezza (lunghezza, temperatura, ecc.) con
l'analoga proprietà (grandezza) del misurando. Il
risultato di quest'operazione di confronto è un
numero puro (misura) e rappresenta quante volte
l'unità di misura prescelta è contenuta nel
misurando.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Metodi di misurazione
Metodo diretto di misurazione:metodo di misurazione
nel quel il valore del misurando è ottenuto
direttamente piuttosto che mediante misurazioni di
altre grandezze legate funzionalmente al misurando
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Metodo indiretto di misurazione:metodo di
misurazione nel quale il valore del misurando è
ottenuto mediante misurazione di altre
grandezze legate funzionalmente (legge fisica)
al misurando, esempi: misura della velocità
dalla misura di spazio e tempo, v = s/t),
misura della pressione da misure di massa,
accelerazione di gravità locale, superficie e
temperatura (p=  Mi gl/A(t))
F= Mi gL
Anita Calcatelli
A(cm2)
2013 -2014:Formazione&Metrologia
Trasduttore a indice
Capsule Dial Gauge, Force
Gauge scale
Leak-tight case
Connection
to system
Hollow
capsule
Mechanical
linkage
Elemento sensibile
dispositivo, impiegato in
una misurazione, che
fornisce una grandezza di
uscita avente una
relazione specificata con
la grandezza di ingresso
Membrane
capacitive
Serie di trasduttori di pressione:
p =f(spostamento dell’elemento sensibile)
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Vacuometro a ionizzazione
collettore
griglia
trasduttori
Termocoppia,
trasformatore di
corrente
elettrica,
estensimetro,
elettrodo per la
misurazione del
pH,…..
filamento
ioni = corrente positiva = f(p)
ip = kiep
k= N =  
 = probabilità di ionizzazione
coefficiente di ionizzazione
= libero cammino medio degli
elettroni
Tutti questi trasduttori e
molti altri ancora vanno
tarati per confronto con un
sistema primario o con altro
trasduttore tarato.
Anita Calcatelli
p =S x ip
S=sensibilità
2013 -2014:Formazione&Metrologia
in definitiva
la misura è
il valore numerico associato al misurando
mediante la misurazione
Esso deve essere accompagnato dall’unità
di misura
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Errore di misura : differenza tra il risultato di una
misurazione ed il valore del misurando ritenuto
convenzionalmente vero.
Il valore vero non è mai noto; si può assumere
come valore vero quello del campione di
riferimento, detto appunto valore vero
convenzionale.
L’errore è un concetto ideale del quale si può fare
una stima e può, eventualmente, rientrare
nell’incertezza
o di cui si deve valutare il valore
dell’incertezza.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Gli errori casuali non sono definibili a priori ma si
possono ridurre aumentando il numero delle
misurazioni in modo che la loro media sia più vicina
possibile alla speranza matematica o valore atteso.
Anche l’errore sistematico non può essere eliminato
ma lo si può ridurre.
Ad esempio se l’effetto della temperatura sul
risultato di una misurazione è importante lo si dovrà
quantificare in modo da apportare la correzione con
la sua incertezza.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Incertezza di misura: stima caratterizzante il campo
di valori entro i quali cade il valore più probabile del
misurando.
DUNQUE
Incertezza di misura = parametro
associato al risultato di una misurazione,
che caratterizza la dispersione dei valori
ragionevolmente attribuibili al misurando.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
E’ importante non confondere l’errore con
l’incertezza
Anita Calcatelli
2013 -2014:Formazione&Metrologia
in definitiva come risultato di una
misurazione la sola
misura non è sufficiente
oltre al valore numerico associato al
misurando mediante la misurazione occorre
fornire un altro valore numerico che è
l’incertezza
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Ma non basta ancora
Occorre anche attribuire il livello di confidenza che
stabilisce “quanto siamo sicuri che il valore dato
(misura) cada entro i margini rappresentati
dall’incertezza”.
Dunque il risultato di una misurazione, per esempio
della lunghezza di una sbarra, sarà espresso nel
modo seguente:
20 cm  1 cm al livello di confidenza del 95 %
O meglio ancora L = 20 cm u(L) = 1 cm, k =2
Ciò vuol dire che siamo sicuri al 95% che la
lunghezza del pezzo considerato é compresa tra
19 cm e 21 cm.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
una misura si compone essenzialmente di una
quaterna di informazioni:
1. il valore numerico relativo alla misurazione (misura)
2. l’unità di misura con la quale si é effettuata la
misurazione
3. l’incertezza con la quale si fornisce il valore della
misurazione
4. Il livello di confidenza
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Nel definire il livello di confidenza o probabilità
di copertura si parla di probabilità; essa va
definita nel modo più immediato possibile.
“la probabilità che si verifichi un certo evento
(esempio l'uscita del numero 5 nel lancio di un dado)
può essere vista come il rapporto tra il numero dei
casi favorevoli ed il numero dei casi totali (possibili),
purché questi ultimi siano tutti ugualmente probabili”.
cioé
la probabilità è un numero compreso tra 0 e 1:
* un evento che non può verificarsi ha probabilità zero;
* un evento che si verificherà sicuramente ha probabilità 1;
* tutte le situazioni intermedie hanno probabilità
compresa tra i valori 0 e 1.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Supponiamo di dover valutare la qualità di un
processo produttivo di un certo prodotto esaminando
la costanza di un parametro significativo del
prodotto stesso.
Per es il peso effettivo di 25 426 confezioni di
Nutella (un campione significativo dell’intera
popolazione delle confezioni di Nutella) aventi peso
nominale 1 kg.
Quante confezioni hanno un peso compreso tra
995 g e 1005 g?
Anita Calcatelli
Saremo tanto più soddisfatti quanto
più alta sarà la frazione che cade
nell’intervallo tra 995 g e 1005 g.
2013 -2014:Formazione&Metrologia
Se 1436 confezioni soddisfano il requisito, diremo
che la frequenza con cui una confezione di Nutella
da 1 kg ha un peso effettivo compreso tra 995 g e
1005 g è n=1436/25426=0,056
Potremo costruire un grafico dividendo
il campo di valori di peso compresi tra il
massimo (1040 g) ed il minimo (940g) in 20
intervalli di ampiezza 5 g.
* calcolando la frequenza che compete a
ciascun intervallo.
*Costruendo un diagramma
cartesiano nel quale riportiamo in ascissa i 20
intervalli in successione ordinata crescente ed
Anita Calcatelliin ordinata le 20 frequenze corrispondenti.
2013 -2014:Formazione&Metrologia
Densità di probabilità: si supponga ora
di aumentare le dimensioni del campione
fino a comprendere l’intera popolazione,
facendo tendere ad infinito nel
contempo il numero dei sottointervalli e
riducendone l’ampiezza a zero.
E’intuitivo che l’istogramma
tenderà ad una curva
continua che rappresenta la
densità di probabilità p(x)
del peso di una confezione
di Nutella.

Diremo dunque che il peso effettivo di una confezione di
Nutella è una variabile casuale che segue una certa
distribuzione sulla cui forma abbiamo acquisito qualche
informazione grazie all’indagine effettuata sul
campione.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Ripetibilità delle misure
grado di concordanza tra i risultati di successive
misurazioni condotte in modo da rispettare le
seguenti condizioni:
stesso metodo di misurazione
stesso osservatore
stesso strumento di misurazione
stesso luogo
stesse condizioni di utilizzazione
Anita Calcatelli
ripetizione entro un periodo di tempo breve
2013 -2014:Formazione&Metrologia
Riproducibilità
Stabilità
grado di concordanza tra i risultati di misurazioni
dello stesso misurando quando le singole misurazioni
sono condotte cambiando condizioni, come:
metodo di misurazione
osservatore
strumento di misurazione
luogo
condizioni di utilizzazione
Anita Calcatelli
tempo
2013 -2014:Formazione&Metrologia
Varianza sperimentale delle osservazioni=
indice di dispersione delle misure
i n
s 
2
i 1
x i   
2
n 1
dove xi è il risultato della i-esima misurazione
 è la media aritmetica degli n risultati
considerati, n-1 sono i gradi di libertà.
1 i n
   xi
n i 1
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Scarto tipo sperimentale
parametro che caratterizza la dispersione dei
risultati per una serie di n misurazioni dello stesso
misurando, ottenibile dalla formula:
s
i n
1
 xi   

(n  1) i 1
2
Quindi è la radice quadrata della varianza.
Media e scarto tipo sperimentale hanno la
stessa unità di misura.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
La varianza sperimentale della media
2
( xi )
s
2
s ( ) 
n
e lo scarto tipo sperimentale della media
s ( xi )
s( ) 
n
quantificano quanto bene la media  stimi il
valore atteso del misurando.
Anita Calcatelli
Si riferiscono a valutazioni indipendenti del
misurando
2013 -2014:Formazione&Metrologia
mentre
Varianza e scarto tipo sperimentale
caratterizzano la variabilità dei valori
osservati xi ovvero la loro dispersione
intorno alla media 
Anita Calcatelli
2013 -2014:Formazione&Metrologia
La conoscenza dello scarto tipo sperimentale è
un primo passo per avere un’idea della qualità
di una misura o di un insieme di misure.
Esempio: dieci risultati di misurazione di una sbarra (cm)
16, 19, 18, 16, 17, 19, 20, 15, 17, 13
media= 17 cm
Le differenze di ciascun valore rispetto alla media sono:
-1,+2,+1, -1, 0,+2, +3, -2, 0, -4
I quadrati
1,4,1,1,0,4,9,4,0,16
e quindi
1  4  1  1  0  9  4  0  16 40
s 

 4,44cm 2
10  1
9
2
Anita Calcatelli
La stima di s è:
s  4,442,1 cm
2013 -2014:Formazione&Metrologia
Taratura
Tutti gli strumenti vanno tarati
Tarare uno strumento significa confrontarne i valori della
grandezza in uscita con quelli di un’altra analoga misurata
con strumentazione direttamente riferita ad un campione
primario e quindi al Sistema Internazionale di unità di
misura (http://www.inrim.it/ldm/index_i.shtml)
Una catena di riferibilità può essere così definita:
In questo modo uno strumento di lavoro è
direttamente riferito al SI.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
LUNGO LA CATENA, DAL LABORATORIO PRIMARIO,
DOVE RISIEDONO I CAMPIONI PRIMARI, FINO AGLI
STRUMENTI DI LAVORO USATI NELLA VITA DI OGNI
GIORNO (DAI LABORATORI DI RICERCA ALLA
PRODUZIONE,
ALLA
VENDITA)
TALVOLTA
DIRETTAMENTE TALVOLTA PASSANDO ATTRAVERSO
LABORATORI ACCREDITATI PER GLI INTERMEDIARI
DEGLI STRUMENTI DI TRASFERIMENTO, SI HA UN
AUMENTO DEL VALORE DELL’INCERTEZZA, CHE VA
ACCURATAMENTE VALUTATA IN TUTTI I PASSAGGI
RICHIESTI.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
di unobiunivoca
strumento
di ogni
misura
Curva Diagramma
di taratura:di étaratura
la relazione
tra
valore letto
dallo strumento (valore di uscita) e il valore misurato con uno
strumento tarato.
Certificato di taratura (o rapporto di taratura): documento in
cui è registrato il risultato di una taratura.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Torniamo all’incertezza
Concetti di base ed esempi
Da che cosa deriva l’incertezza?
- Strumento di misura (bias, invecchiamento, drift,
scarsa ripetibilità
- Oggetto da misurare, non stabile (es. si pensi di
misurare l’altezza di un blocco di ghiaccio in
una stanza riscaldata)
- Processo di misurazione, può essere complesso (es.
altezza di un piccolo animale in movimento….)
- Incertezza importata, per es. data nel certificato
di taratura
Anita Calcatelli
2013 -2014:Formazione&Metrologia
- Capacità dell’operatore, alcune misure
dipendono dalla capacità di discernimento o
condizione psico-fisica dell’operatore
(leggere la posizione di un indice su una
scala graduata).
- Campionamento, ad esempio se si debbono
misurare alcuni pezzi provenienti da una linea di
produzione è buona prassi evitare, per il
campionamento, di prendere i primi pezzi
prodotti il lunedì mattina
- Ambiente, variazioni di temperatura,
pressione, umidità, …
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Cos’è il modello di una misurazione?
Con il modello descriviamo le
relazioni tra ciò che ci interessa
conoscere e ciò che misuriamo.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Importanza del modello
•
•
•
Rappresentiamo tutta la realtà mediante
modelli.
Le misure forniscono rappresentazioni
quantitative della realtà: quindi dobbiamo
rappresentare la misura mediante un
modello.
Il modello schematizza l’oggetto o il
fenomeno del quale vogliamo conoscere una
caratteristica o una proprietà.
Per poter misurare bisogna conoscere
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Conoscere per saper indicare il
modello corretto o più adatto
1. La conoscenza deve spingersi fino a:
rappresentare la caratteristica o proprietà da
misurare con il dettaglio necessario; necessario
per poter eseguire le misure.
2. Riconoscere che scegliamo un modello
approssimato e che questa approssimazione
costituisce il limite alla qualità della misura: non
sarà possibile una qualità migliore
dell’approssimazione effettuata tramite la
modellizzazione.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Incertezza del modello
A tale limite si dà il nome di incertezza
del modello. Esempi:
1. Misurare il volume di un barattolo
mediante la misura di un diametro e di
una altezza (la forma del barattolo si
scosta da quella del cilindro)
2. Misurare la temperatura di una stanza
mediante un termometro posto su una
parete (la temperatura varia da punto
a punto nella stanza)
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Misurare per decidere
tutti i giorni prendiamo delle
decisioni
Devo affrettarmi per arrivare in tempo
all’appuntamento? (un limite)
Devo preoccuparmi per i risultati di un esame
clinico? (due limiti)
Quanti metri quadri di moquette devo acquistare
per coprire il pavimento?
E’ giusto pagare ciò che mi chiede il venditore di
benzina?
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Misurare per decidere
Le decisioni in forma grafica
Se la misura cade
entro questi valori
allora è SI
Se cade qui
è NO
Anita Calcatelli
Se cade qui
è NO
2013 -2014:Formazione&Metrologia
L’incertezza: il modo scientifico di
descrivere la qualità di una misura
Nella vita corrente usiamo molte altre parole
per esprimere la qualità delle misure:
LE PAROLE
• Misura precisa, accurata, affidabile, ecc.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Incertezza e decisione
1. E’ esperienza comune quella di compiere
una misura con maggiore o minore cura a
seconda del tipo di decisione che si deve
assumere in base al risultato. Esempi:
misurare l’ora per decidere se accelerare;
misurare la massa di un alimento per
decidere se pagare il richiesto.
2. Pertanto prima di iniziare a compiere una
misura ci prefiggiamo un’incertezza
necessaria, un obiettivo (target).
Anita Calcatelli
2013 -2014:Formazione&Metrologia
I due limiti dell’incertezza
1. Limite inferiore: l’incertezza del modello che
intendiamo utilizzare
2. Limite superiore: l’incertezza obiettivo, al di
sopra della quale risulta impossibile l’uso del
risultato (per decidere o altro)
CONCLUSIONE
L’incertezza che ci consentono i mezzi coinvolti
nella misurazione (che comprende l’incertezza di
modello) deve cadere entro tali due limiti
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Modi di esprimere l’incertezza di
una misura esplicitamente
Mediante intervalli deterministici
• Con una frazione della tolleranza pretesa
per la utilizzabilità del prodotto
• Con l’errore massimo (scostamento dal nominale) ammesso (correlato alla
tolleranza), o l’errore limite ammesso
(inquinamento)
• Mediante limiti di variabilità (analisi
cliniche)
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Modi di esprimere la qualità
di una misura esplicitamente
Mediante l’incertezza
• L’uso del concetto e del termine di incertezza è
obbligatorio quando si vuole esprimere in modo
quantitativo la qualità di una misura.
PERCHE’?
INCERTEZZA: indicatore quantitativo del grado di
fiducia attribuito ad una misura
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Perché l’incertezza?
1. E’ l’unico modo accettato a livello
internazionale
2. E’ definita una matematica che
consente di combinare tra loro
incertezza provenienti da fonti diverse
3. L’incertezza “scientifica” è associata a
concetti probabilistici e quindi ci
consente di valutare i rischi connessi
alla successiva decisione
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Cause di incertezza
1. L’ambiente
2. Campioni e strumenti di misura impiegati
3. L’apparato di misura
4. L’organizzazione della misurazione
5. Il software di misura
6. L’operatore
7. Natura e incertezza del misurando
8. Il modello adottato
9. La procedura di misurazione
10. ……………….
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Cause di incertezza
Aspetti didattici
1. Provare a far ripetere la misura
•
più volte dalla stessa persona
•
da persone diverse
2. Iniziare a fare delle medie, per singola
persona e tra persone diverse
• discutere delle cause della dispersione
• come indicare quantitativamente la
dispersione?
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Cause di incertezza
Come rappresentarle nel modello?
Passiamo al modello di una misura diretta:
M
corretta=M proposta da strumento
+ C1 + C2 + C3 + ..
Se C1=C2=C3= 0
L’ipotesi che le correzioni siano nulle NON SIGNIFICA
che si tratti di una ipotesi senza incertezza!
non è
u(C1 )=0, u(C2 )=0, u(C3)=0
Con u(x) indichiamo l’incertezza di x (u da uncertainty)
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Cause di incertezza
Aspetti didattici della
rappresentazione
È importante chiarire che
quando si formula
un’ipotesi, anche di zero,
essa è sempre affetta
da un’incertezza.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Aspetto principale del
concetto di incertezza
Ad ogni informazione utilizzata
nel calcolare il valore
misurato è associata una
incertezza.
Ad ogni incertezza è associata
una distribuzione di
probabilità.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Due categorie di incertezze: A
Categoria A
La stima della grandezza è ottenuta
sulla base di analisi statistica di
serie di osservazioni. L’incertezza
tipo è valutata mediante lo scarto
tipo sperimentale della distribuzione
o mediante lo scarto tipo della
media.
Per calcolare media e scarto tipo si ricorre alla
statistica
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Due categorie di incertezze: B
Categoria B
La stima del valore di questa componente è ottenuta con altri
metodi.
L’incertezza tipo è valutata per mezzo di un giudizio basato su
tutte le informazioni disponibili sulla possibile variabilità della
grandezza di ingresso considerata.
L’insieme delle informazioni può comprendere: dati di misurazioni
precedenti; esperienza o conoscenza generale del
comportamento e delle proprietà dei materiali e strumenti di
interesse; specifiche tecniche del costruttore; dati forniti in
certificati di taratura o altri; incertezze assegnate a valori di
riferimento presi da manuali.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Incertezza tipo
•
•
•
Incertezza tipo (standard uncertainty)
u(x): incertezza di una stima x espressa
come scarto tipo u(x)  s(x) della
distribuzione di probabilità associata.
Valutazione (dell'incertezza) di categoria A
(Type A uncertainty evaluation): metodo di
valutazione dell'incertezza per mezzo dell'analisi
statistica di serie di osservazioni
Valutazione (dell'incertezza) di categoria B
(Type B uncertainty evaluation): metodo di
valutazione dell'incertezza con mezzi diversi
dall'analisi statistica di serie di osservazioni
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Incertezza composta ed estesa
•
•
Incertezza composta u(M): incertezza di
una stima del misurando M espressa come
scarto tipo u(M)  s(M) della distribuzione di
probabilità associata al misurando.
Incertezza
estesa
U(M): incertezza
composta moltiplicata per un fattore di
copertura k (tra 1,5 e 3). L’intervallo
costituito da ± U(M) si chiama intervallo di
confidenza e a esso è associato un
coefficiente
di
fiducia,
ossia
una
probabilità che entro tale intervallo
cadano una percentuale calcolabile di
valori misurabili.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Scarto tipo di una
distribuzione
Lo scarto tipo (o scarto quadratico medio o
deviazione standard) è un indice di dispersione
delle misure sperimentali xi. Se x soprasegnato
è il valore medio della distribuzione:
allora lo scarto tipo σx è calcolato come:
Se n è
grande
Anita Calcatelli
2013 -2014:Formazione&Metrologia
La varianza di una
distribuzione
La varianza σx2 di una distribuzione
è il quadrato dello scarto tipo della
distribuzione.
non ha senso combinare tra loro
gli scarti tipo.
È invece possibile
sommare tra loro le varianze.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Se si sommano tra loro le
varianze di una
distribuzione di
probabilità, il risultato è
ancora la varianza di una
distribuzione.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
La varianza di una variabile aleatoria non è mai
negativa ed è zero solo quando la variabile assume
quasi certamente un solo valore.
Tentativo di spiegazione
La varianza di x è definita come il valore atteso del
quadrato della variabile aleatoria centrata [x-E(x) ]1
V(x) =E[x-E(x)]2 e V(y) =E[y-E(y)]2
E per x+y
V(x+y)= E[(x-E(x)]2+E[(y-E(y)]2+ 2 (x-E(x)]*[y-E(y)]=
=E[x-E(x)]2+E[y-E(y)]2+2 [(x-E(x))*(y-E(y)]=
=V(x)+V(y)+2 cov (x,y)
Termine di
covarianza
---------------------------------------------------------------------------
1
in teoria delle probabibilità il valore atteso (valore medio, speranza, speranza matematica) di una variabile
acsuale x è un numero indicato con E(x) (expected value)
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Analogamente per x-y
V(x-y) =V(x)+V(y)+2 cov (x,y)
Il contributo
negativo è
contenuto in
questo termine
Se non c’è correlazione il termine 2 cov (x,y) va a
zero e
V(x+y) = V(x)+V(y)= V(x-y)
Ossia 2(x+y) = 2(x) + 2(y)
Anita Calcatelli
2013 -2014:Formazione&Metrologia
In genere lo
rappresentiamo così:
σx2 + σy2 = σc2
Cx2 ·
σx2 + cy2 · σyb2 = σd2
Non è vero che
Anita Calcatelli
σa + σb = σc
2013 -2014:Formazione&Metrologia
Legge di propagazione delle
incertezze
Sostituiamo i vecchi simboli
così: σx=u(x); σy=u(y); ecc.
Cx2 · u2 (x) + cy2 · u2 (y) =
2
u (c)
cx e cy si chiamano coefficienti
di sensibilità.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Cosa sono i coefficienti di
sensibilità
Sono il “peso” con cui ogni singola
causa di incertezza contribuisce a
produrre l’incertezza complessiva.
Si calcolano variando una sola delle
grandezze (quella alla cui
incertezza è abbinato il c in esame)
e vedendo come varia il risultato.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Esempio 1: misura del peso netto
Modello: peso netto = peso lordo –
tara -> pn = pl – t
Procedura: misuro con bilance pl e t e,
con l’equazione di modello, calcolo pn.
Calcolo del risultato della misura:
se pl=6,2 kg e t=0,3 kg, pn=5,9 kg
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Esempio 1: definiamo l’incertezza
obiettivo
Dipende evidentemente dal tipo di
alimento che intendo acquistare e
da quanto considero trascurabile
la frazione di euro che viene
messa in dubbio dall’incertezza
della misura.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Esempio 1: definiamo l’incertezza obiettivo
Considero trascurabile € 0,05 (scarti)
Caso A: compro qualcosa che vale 2 €/kg
(finocchi). L’incertezza obiettivo sulla massa
sarà 25 g (0,05/2)
Caso B: compro qualcosa che vale 0,5 €/kg
(patate). L’incertezza obiettivo sulla massa sarà
100 g (0,05/0,5)
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Esempio 1: quale decisione devo
prendere?
Pagare il richiesto, oppure
chiedere una misura più
precisa o uno sconto
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Torniamo all’esempio del peso netto e
lordo e calcoliamo l’incertezza
Modello:
pn = pl – t
Incertezza
u2(pn)=c12(pl)·u2(pl)+c22(t)·u2(t)
c1 e c2 ?
pesi
ATTENZIONE: si perde il segno perché
tutto è al quadrato
Anita Calcatelli
2013 -2014:Formazione&Metrologia
calcoliamo i pesi
u2(pn)=c2(pl)·u2(pl)+c2(t)·u2(t)
È evidente che tutti i pesi valgono
1; basta immaginare di variare
uno solo degli u di una grandezza
di ingresso e si vede subito che la
u2(pn) varia di altrettanto.
La regola vale per tutti i modelli
costituiti solo da somme o differenze
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Se c2(pl)=1 e c2(t)=1 allora il
modello per il calcolo
dell’incertezza si semplifica:
u2(pn)=u2(pl)+u2(t)
Per stimare u2(pl) e u2(t) bisogna
conoscere le caratteristiche
della bilancia (conoscere per
misurare!).
Anita Calcatelli
2013 -2014:Formazione&Metrologia
studiamo la bilancia
Cause d’incertezza nella bilancia:
1. insensibilità, dovuta agli attriti
2. errata taratura
3. se con una molla:
• effetto della temperatura
• effetto dell’altitudine
4. Altre? (non ci sono solo
incertezze dovuta alla bilancia!)
Anita Calcatelli
2013 -2014:Formazione&Metrologia
incertezza della bilancia
Si va a “naso”?
sarà non inferiore alla più piccola
divisione leggibile sulla scala e non
superiore a circa 10 volte tanto.
Ipotizziamo
ubilancia= u (pl)=u (t)= 50 g=0,05 kg
Risultato: u2(pn)=u2(pl)+u2(t)
u (pn)=1,41·0,05 kg ≈0,07 kg=70 g
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Quando ignorare le covarianze
porta ad una sovrastima
dell'incertezza
•  T = T1 - T2
• Stesso termometro: u(T1 ) = u(T2 ) =
1 °C
• u2 (T) = u2 (T1 ) + u2 (T2 ) = 12 + 12 = 2 °C
NO
• u2 (T) = u2 (T1 ) + u2 (T2 ) – 0,8 u(T1 )
u(T2 ) = 12 + 12 – 0,8 = 1,2 °C;
Anita Calcatelli
2013 -2014:Formazione&Metrologia
quando ignorare le covarianze
porta ad una sottostima
dell'incertezza
• Due campioni di massa M1 ed M2 da 1 kg
• u(M1 ) = u( M2 ) = 0,1 g; tarati con lo stesso
campione
• M = M1 + M2 = 2 kg; u(M) ?
• Ignorando covarianze u(M) = 0,14 g
• u2 (M) = u2 (M1 ) + u2 (M2 ) + 0,8 u(M1 ) u(M2 ) =
0,12 + 0,12 + 0,8  0,1  0,1 = 0,028;
• u(M) = 0,17 g
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Le decisioni in presenza di incertezze
Limite inferiore
SI
NO
Limite superiore
NO
Fase di
verifica
2u
Zona
Zona di Ambigua
NO certo
Anita Calcatelli
Zona di SI certo
2u
Zona
Ambigua
Zona di
NO Certo
2013 -2014:Formazione&Metrologia
Aspetti didattici
I concetti fondamentali sono:
1. L’incertezza è un’informazione
essenziale da fornire insieme al
risultato di misura.
2. Si compie una misurazione con uno
scopo. Prima di iniziare il processo
sperimentale bisogna conoscere lo
scopo e l’incertezza massima
accettabile per conseguirlo.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Aspetti didattici
3.
Ogni informazione, sperimentale o
ottenuta da altra fonte, usata per ottenere
il risultato di misura è associata a una
incertezza, anche se l’informazione ha
valore zero.
4. L’incertezza è rappresentata associando a
ogni informazione una distribuzione di
probabilità.
5. Una distribuzione di probabilità è definita
mediante il suo valore medio e la sua
varianza.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Aspetti didattici
La distribuzione di probabilità con la quale si ha a che fare più
spesso è la distribuzione normale o gaussiana.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Aspetti didattici
7. Dalla figura precedente si
deduce che:
• Più grande è la varianza, più larga è la
distribuzione.
• Fattore di copertura: Valgono le seguenti
relazione, solo per la distribuzione
normale:
68,3% = P{ μ - σ < X < μ + σ }
95,5% = P{ μ - 2 σ < X < μ + 2 σ }
99,7% = P{ μ - 3 σ < X < μ + 3 σ }
Anita Calcatelli
2013 -2014:Formazione&Metrologia
9. Le relazioni prima elencate
definiscono, per ciascun FATTORE
DI COPERTURA k (k=1, 2, 3, il
fattore di moltiplicazione di σ) la
probabilità che il valore misurato
cada nell’intervallo, intorno al valore
medio, definito dal prodotto tra il
fattore scelto e lo scarto tipo
(incertezza tipo) della distribuzione.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Fattore di copertura k
È il fattore numerico usato come
moltiplicatore dell'incertezza tipo
composta (ossia finale della misura)
per ottenere un'incertezza estesa.
U  y   k  uc  y 
Anita Calcatelli
2013 -2014:Formazione&Metrologia
incertezze relative
Si consiglia di esprimere
l’incertezza in forma relativa,
cioè divisa per il valore al quale si
riferisce, SOLO alla fine dei
calcoli della stima, ossia
sull’incertezza composta ed
eventualmente estesa.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Esempi ed esercizi
Misura dell’area di una superficie
rettangolare mediante la misura
della lunghezza della base e di
quella dell’altezza
Altri suggeriti dai partecipanti
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Incertezza di una somma, in prima approssimazione Sui vostri testi
Somma di segmenti :
u(a)
u(b)
a
b
u(a)
a con u(a) e b con u(b)
amax = a + u(a) a min = a-u(a)
bmax = b + u(b) bmin =b-u(b)
x = a +b
u(b)
modello
xmax =amax + bmax x min = amin + bmin
u(x) =
xmax – xmin
=
[a+u(a)+b+u(b)] – [a-u(a)+b-u(b)]/2
2
u(x) =[ 2u(a) + 2u(b)]/2 = u(a) + u(b)
In realtà u2(x)=u2(a)+u2(b) + corrv u(a)u(b)
E se non' c’è
correlazione
u ( x)  u 2 (a )  u 2 (b)  corr (u (a )u (b)esenonc
ècorr
u ( x)  u 2 ( x)  u 2 ( y )
Anita Calcatelli
Non è la stessa
cosa
2013 -2014:Formazione&Metrologia
Incertezza di un prodotto (superficie)
a con u(a) b con u(b)
x max  a max  b max

x min  [( a  u ( a ))  ( b  u ( b ))]
x min  [ a  u ( a )  ( b  u ( b )]
u(x) =[umax-umin]/2
u(x) = a u(b) + bu(a)
In realtà dovrei scrivere
u2(x)= a2u2 (b) + b2 u2(a) + corr u( a)u(b)
Anita Calcatelli
u2(x)= a2u2 (b) + b2 u2(a) e non tenendo conto
della correlazione
2013 -2014:Formazione&Metrologia
Prodotto di tre segmenti (volume)
a con u(a)
b con u(b) c con u(c)
Come esercizio svolgere
Risultato
u (V )  bcu ( a )  acu (b )  abu (c )
E in relativo
Anita Calcatelli
u (V ) u (abc) u (a ) u (b) u (c)




V
abc
a
b
c
2013 -2014:Formazione&Metrologia
Rapporto di grandezze: densità
d
Misurazioni indipendenti di
volume e massa
massa M

volume V
d max  d min
u (d ) 
2
d max
d min
M min M  u ( M )


Vmax
V  u (v )
M max M  u ( M )


Vmin
V  u (V )
In realtà
1 2
M2 2
 (d )  2  ( M )  4  (V )
V
V
2
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Equazione della misurazione
Nella maggior parte dei casi il misurando, Y, non è
misurato direttamente ma è valutato mediante n altre
grandezze X1, X2, . . . , Xn attraverso una funzione
f, o equazione della misura (relazione tra grandezze)
Y= f(X1,X2,…..Xn)
[1]
Tra le grandezze Xi sono incluse correzioni (o fattori di
correzione) e grandezze che tengono conto di altre sorgenti di
variabilità (osservatori differenti, strumenti, campioni, laboratori,
tempi in cui le osservazioni sono state fatte (per es. in giorni
diversi).
Questa equazione non esprime semplicemente una legge
fisica ma un processo di misurazione ed essa dovrebbe
contenere tutte le grandezze che possono dare un
contributo significativo all’incertezza da attribuire al
risultato della misurazione.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Una stima del misurando o grandezza d’uscita,y,
si ottiene applicando l’equazione Y= F(X1,X2,…..Xn)
e usando come grandezze d’ingresso le stime
x1,x2,. .,xn
per i valori delle n grandezze
d’ingresso X1, X2, . . , Xn.
Quindi la stima d’uscita y, che è il
dell’operazione di misurazione, è data da
y = f(x1, x2, . . . , xn)
risultato
[2]
Le xi sono grandezze di ingresso i i cui valori
influenzano e/o determinano il risultato della
misura.
y è la grandezza d’uscita il cui valore siamo
interessati
a conoscere mediante misure. 2013 -2014:Formazione&Metrologia
Anita Calcatelli
esempio
La velocità con cui si muove un corpo si valuta
mediante misurazioni di spazio e di intervallo di
tempo
v = L/t
Nel calcolare l’incertezza tipo di v si dovranno
valutare le componenti dovute alle due
misurazioni,di spazio percorso e intervallo di tempo
necessario per percorrerlo.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
esempio,
se viene applicata una differenza di potenziale
V agli estremi di un resistore dipendente dalla
temperatura il quale ha una resistenza R0 ad
una determinata temperatura t0 ed ha un
coefficiente di dilatazione lineare b, la potenza
dissipata P (misurando) dal resistore alla
temperatura t dipende da V, Ro, b e t secondo
la relazione
P = f(V, R0, b, t) = V2/R0[1 + b(t - t0)]
Anita Calcatelli
[3]
2013 -2014:Formazione&Metrologia
In sintesi
- Incertezza tipo: incertezza del risultato di una
misurazione espressa come scarto tipo
- Valutazione dell’incertezza di categoria A: metodo
di valutazione per mezzo dell’analisi statistica di
serie di osservazioni. E’ caratterizzata dalla
varianza stimata e dal suo scarto tipo sperimentale
-Valutazione dell’incertezza di categoria B: metodo di
valutazione dell’incertezza con mezzi diversi dall’analisi
statistica dei risultati. Debbono essere caratterizzate
da grandezze ui2 che sono trattate come varianze..
Anita Calcatelli
2013 -2014:Formazione&Metrologia
- incertezza tipo composta: incertezza tipo del
risultato di una misurazione che è ottenuto
come media di valori di un certo numero di
altre grandezza; è eguale alla radice
quadrata positiva di una somma di termini che
sono la varianza delle grandezze che
intervengono
- incertezza estesa: grandezza che definisce un
intervallo che si pensa comprenda una frazione
rilevante della distribuzione dei valori
ragionevolmente attribuibile al misurando
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Classificazione delle componenti dell’incertezza
L’incertezza tipo composta del risultato di una
misurazione, y, deriva dalle incertezze u(xi) (o
semplicemente ui) delle stime di ingresso xi che
entrano nell’equazione
y = f(x1, x2, . . . , xn)
[2]
Nell’esempio dell’equazione
P = f(V, R0, b, t) = V2/R0[1 + b(t - t0)]
[3]
l’incertezza tipo composta del valore stimato della
potenza P deriva dalle incertezze delle stime della
differenza di potenziale V, della resistenza Ro, del
coefficiente di temperatura b e della temperatura t.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
In genere le varie componenti dell’incertezza si possono
raggruppare in due categorie in base al metodo seguito
per la loro valutazione.
Ciascun componente dell’incertezza, comunque valutata,
è rappresentata da uno scarto tipo stimato, detta
incertezza tipo (ui) ed è eguale alla radice quadrata
della stima della varianza.
L’incertezza del risultato di una misurazione
rispecchia l’incertezza sulla conoscenza esatta del
misurando.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Tipi generali di incertezza che si verificano in
ogni risultato di misurazione
Random /casuale), o di categoria A ,
caratterizzata dalla varianza sperimentale
si2 e relativo scarto tipo sperimentale si
Sistematico, o di categoria B, che deve essere
caratterizzata da grandezze ui2che sono
trattate come varianze si2
Questa classificazione ha semplicemente validità
didattica, non implica l’esistenza di differenze nella
natura delle componenti risultanti dai due tipi di
valutazione.
Entrambe i tipi di valutazione sono basati su
di probabilità.
Anitadistribuzioni
Calcatelli
2013 -2014:Formazione&Metrologia
In senso lato, l’incertezza può avere un’origine
esterna o può essere ottenuta assumendo una
distribuzione di probabilità. Le distribuzioni
possono essere di vari tipi, ma le più comuni
sono: normale, rettangolare e triangolare.
 p(t )dt  1
a
a
a
a
1/a
1/2a

Anita Calcatelli
aa+

a-  a+
µ è il valore atteso o media della
distribuzione
e le aree tratteggiate
rappresentano ± una incertezza tipo intorno
2013 -2014:Formazione&Metrologia
alla media.
Eseguiamo una serie di misurazioni e riportiamo i risultati in un
grafico. Allo scopo suddividiamo l'asse delle ascisse in intervalli
uguali al valore della risoluzione del nostro strumento, mentre
indichiamo sull'asse delle ordinate il numero degli eventi. Su
tale grafico riportiamo, per ogni misurazione eseguita, un
rettangolo che ha per base il valore ottenuto e per altezza un
evento: disegniamo così la successione degli eventi. Otteniamo
un grafico ad istogramma
Anita Calcatelli
2013 -2014:Formazione&Metrologia
n
risoluzione  0
Nei processi di misurazione in teoria possiamo eseguire
un numero infinito di misure: abbiamo quindi a che fare
con una distribuzione di tipo continuo.
Se aumentiamo di molto il numero delle misurazioni
otteniamo una distribuzione sempre più regolare e
simmetrica rispetto ad un picco d'eventi che risulterà
posizionato in un determinato punto dell'asse delle
ascisse.
Il grafico ha l'aspetto tipico di una gaussiana
Anita Calcatelli
2013 -2014:Formazione&Metrologia
100% di probabilità
t-s
t
t+s
Questa
è
una
tipica
distribuzione
normale
o
gaussiana: in un insieme di
osservazioni la maggior parte
dei valori è più probabile che
cada nell’intorno del valore
medio che lontano da esso.
p(t)= densità di probabilità p (t ) 
1  t  t 
 

2 s 
2
1
Gaussiana
e
s 2
Un esempio tipico è rappresentano dalla
distribuzione delle altezze di alcune persone:
la maggior parte delle persone hanno altezze
vicino alla media; pochi individui sono o
estremamente alti o estremamente bassi.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Quando eseguiamo una serie di misurazioni
ogni volta che aggiungiamo un dato la media si
sposta un pò, cioè si sposta tutta la
distribuzione.
All’aumentare del numero delle misure le variazioni
della media diminuiscono
Anita Calcatelli
2013 -2014:Formazione&Metrologia
La miglior stima del misurando è data
dalla media aritmetica.
1 i n
   xi
n i 1
(*)
E la miglior stima della varianza sperimentale delle
osservazioni è
2
i n



x

(**)
2
i
s 
i 1
n 1
E scarto tipo sperimentale
s
(*)

1
 xi   

(n  1) i 1
   xp( x)dx
Anita Calcatelli

i n
2

s   ( x   ) p ( x)dx
(**) 2

2
2013 -2014:Formazione&Metrologia
E per la media si avrà:
2
Varianza della media
Scarto tipo della media
s ( xi )
s ( ) 
n
2
s ( xi )
s(  ) 
n
Distribuzioni di probabilità di tipo A
richiedono questo trattamento statistico
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Distribuzioni di tipo B
In questa categoria rientrano tutte quelle incertezze
che non possono essere caratterizzate tramite lo
scarto tipo sperimentale di misure ripetute (tipo A).
L’incertezza può essere valutata mediante distribuzioni
di probabilità stabilite sulla base o di una analisi
teorica del processo o di conoscenze sperimentali delle
caratteristiche e del comportamento della
strumentazione presa in esame, specifiche di
fabbrica, certificato di taratura…..
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Nelle valutazioni di tipo B
* Dapprima si fa una stima dei limiti delle variazioni
sulla misura causate da una sorgente di
incertezza, cioè si valuta lo scarto massimo.
* Si assume una certa distribuzione di probabilità tra
questi limiti.
* Si calcola lo scarto tipo equivalente che
rappresenta l’incertezza tipo B.
Normale, rettangolare, triangolare…
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Le informazioni disponibili possono essere:
·conoscenza generale, basata su precedenti esperienze,
del comportamento o delle proprietà di materiali
o strumenti
•specifiche del costruttore
•dati forniti dai certificati di taratura o da altri rapporti
•valori di incertezze ricavate dai manuali
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Valutazione di categoria B dell’incertezza tipo
La valutazione dell’incertezza si basa su metodi diversi
dall’analisi statistica di serie di osservazioni.
Per una stima xi di una grandezza di ingresso Xi
che non è stata ottenuta da osservazioni ripetute,
i
valori
della
varianza
stimata
u2(xi)
o
dell’incertezza
tipo
u(xi)
sono
basati
su
considerazioni di tipo scientifico utilizzando tutte
le informazioni disponibili.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Il corretto uso delle informazioni disponibili per la
valutazione di categoria B dell’incertezza tipo
richiede intuizione basata sull’esperienza e sulla
conoscenza generale.
Questa è una capacità che può essere acquisita
con la pratica. Una ben fondata valutazione di
categoria B può essere attendibile quanto una di
categoria A,specialmente in una situazione
sperimentale in cui la valutazione di categoria A
sia basata su un piccolo numero di osservazioni
indipendenti.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Quando sia noto un solo valore della grandezza
Xi, cioè una sola misura, (il risultato di una
misura precedente, un valore di riferimento
tratto dalla letteratura, o il valore di una
correzione); questo sarà usato come xi.
Quando sia nota, sarà associata a xi, l’incertezza
tipo u(xi).
Altrimenti essa sarà calcolata da dati di
incertezza non ambigui.
Se dati di questo genere non sono disponibili,
l’incertezza sarà valutata sulla base dell’esperienza.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Quando per la grandezza Xi, si possa assumere
una distribuzione di probabilità basata sulla
teoria o sull’esperienza, la stima xi e
l’incertezza u(xi) saranno il valore atteso della
distribuzione e la radice quadrata della sua
varianza rispettivamente.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Distribuzione normale
Si utilizza quando si ritiene che sia maggiore la
probabilità di trovare valori prossimi alla media
La relazione tra incertezza tipo u
(o scarto tipo equivalente) e i
limiti di variazione (scarto massimo
2a), si calcola osservando che
essendo 2u=a si ha
-a

Anita Calcatelli
+a
a
u   0,5 a
2
2013 -2014:Formazione&Metrologia
1/2a
p(x)
Distribuzione rettangolare
a
a
s
a
p(x)=1/2 a
per x tra –a e +a
(*)
3
p(x)= 0 fuori da
a
x
+
a
+a e -a
-s
+s
Questa è una distribuzione uniforme o rettangolare:
i risultati delle misurazioni sono distribuiti
(sparpagliati) tra i valori più alti e più bassi.
I limiti di variazione sono rappresentati da +/-a.
1 2
1  x3  a 2

s   p( x)( x   ) dx  
x dx 


2a
2a  3  3
2
(*)


2

essendo  p( x)dx  1
Anita Calcatelli
a
a
L’altezza del rettangolo, p(x) è data da 2a*h =1, h=1/2a
2013 -2014:Formazione&Metrologia
La distribuzione rettangolare è una descrizione
ragionevole in termini di probabilità di una
conoscenza inadeguata della grandezza d’ingresso
Xi in assenza di altre informazioni oltre i suoi limiti
di variabilità.
Ma se è noto che i valori della grandezza in
questione vicino al centro dell’intervallo di variabilità
sono più probabili dei valori compresi tra i limiti,
una distribuzione triangolare o normale può essere
un modello migliore.
D’altra parte se valori prossimi ai limiti sono più
probabili dei valori vicini al centro dell’intervallo,
una distribuzione a U può essere più appropriata,
Anita Calcatelli
che
non verrà considerata.
2013 -2014:Formazione&Metrologia
o di Simpson: si utilizza
quando la variabile casuale è
definita in un certo
intervallo, ma vi maggiore
probabilità di trovare valori
prossimi al valore medio
piuttosto che lontano da esso
e sia ipotizzabile che essi
decrescano linearmente dal
centro verso gli estremi.
p(x)
Distribuzione trangolare:
La relazione tra l’incertezza
(scarto tipo equivalente) e i limiti
di variazione (scarto massimo +/a) per questa distribuzione è:
Anita Calcatelli
a
a-
-s
a

a+
+s
x
a
s
6
us
a
6
 0,4a
2013 -2014:Formazione&Metrologia
Il fattore moltiplicativo di a per una
distribuzione triangolare è minore di quello
che si ottiene per una valutazione
rettangolare.
Ciò significa che la distribuzione
rettangolare rappresenta, per la stima di
un contributo de incertezza, una assunzione
più conservativa rispetto a quella
triangolare.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Ritorniamo alla valutazione
di categoria A dell’incertezza tipo
La valutazione dell’incertezza si basa su una analisi
statistica di serie di osservazioni.
Una componente dell’incertezza ottenuta da una
valutazione di tipo A è rappresentata da uno scarto
tipo si valutato statisticamente ed è eguale alla
radice quadrata della varianza si2 statisticamente
valutata ed è associata al numero di gradi di
libertà vi. Dunque per questa componente si ha ui
= si.
L’incertezza tipo di categoria A é ottenuta da una
densità di probabilità derivata da una distribuzione di
frequenza.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
La valutazione di categoria A dell’incertezza tipo
può essere applicata quando siano state fatte
diverse osservazioni indipendenti della grandezza
d’ingresso nelle stesse condizioni di misura.
Se il processo di misurazione ha sufficiente
risoluzione si osserverà una dispersione dei
valori ottenuti.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Innanzi tutto si eseguirà la media aritmetica dei
valori delle singole osservazioni xi (i = 1, 2, …, n)
1 i n
   xi
n i 1
L’incertezza di misura associata alla stima xi si valuta
con
la stima della varianza della distribuzione di probabilità
della popolazione: è la varianza sperimentale s²(x) dei
valori xi che è data da
1 i n
2
s x  
  xi   
n  1 i 1
2
Gradi di libertà
La sua radice quadrata (positiva) è lo scarto tipo
sperimentale.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
La migliore stima della varianza della media
aritmetica  è la varianza sperimentale della
media data da
2

s
x
2
s   
n
La sua radice quadrata (positiva) è lo scarto tipo
sperimentale della media.
s
u( ) 
n
L’incertezza tipo u(x) associata alla grandezza
d’ingresso x è lo scarto tipo sperimentale della media.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Esempio:
t/°C
94,5
95,5
96,5
97,5
98,5
99,5
100,5
101,5
102,5
95,5
96,5
97,5
98,5
99,5
100,5
101,5
102,5
103,5
103,5
104,5
104,5
105,5
Valutazione di categoria A da 22
misure di temperatura
La media aritmetica = 100,06) K è
la miglior stima del valore medio
basata sui dati disponibili.
Per lo scarto tipo sperimentale (=
radice quadrata della varianza) si ha
s(ti) = 0,7 °C
E lo scarto tipo sperimentale della media
rappresenta l’incertezza tipo della media:
s (ti ) 0,7
u ( t )  s( t ) 

 0,25C
22
22
Anita Calcatelli
t
100,0
s(ti)
0,7
s(t)
0,3
2013 -2014:Formazione&Metrologia
Se invece dei 22 valori si conoscessero i valori
estremi 96 °C e 104 °C e si sapesse, per
esperienza, che probabilmente si ha una
distribuzione normale con massima probabilità al
centro
Si potrebbe applicare la valutazione dell’incertezza
secondo una distribuzione normale con media
sempre eguale a 100°C con semiampiezza a=4 e
con
u(t)=s(t) =0,5 a = 0,5*4 = 2°C
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Passiamo alla distribuzione
rettangolare
p
a
1
2
a
a
a-
a+
t
s( t )  u ( t ) 
t  a / 3
Anita Calcatelli
a
3
t  a / 3
2013 -2014:Formazione&Metrologia
Riprendiamo il caso delle misure di temperatura
Se invece di avere i 22 risultati delle misurazioni di t
avessimo una informazione più scarsa e che l’unica
ipotesi possibile fosse che t è descritta da una
distribuzione rettangolare simmetrica avente estremo
inferiore uguale a 96 °C ed uno superiore uguale a
104 °C quindi con semi-ampiezza a= (a+-a-)/2=4 °C,
la densità di probabilità è allora
p(t)=1/2 a
p(t)=0
per
a  t  a
al di fuori
La stima di t è il suo valor medio  = 100 °C
L’incertezza di questa stima è
u (  t )  a / 3  4 / 3  4 / 1,73  2,31C
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Distribuzione triangolare
p
Se ci sono delle ragioni per
ritenere che i gradi di fiducia
decrescano linearmente dal
centro verso gli estremi (94
°C e 104 °C), avremmo una
distribuzione triangolare di
semiampiezza a=4, con valore
atteso (media) t = 100 °C e
scarto tipo della media.
s( t )  u ( t ) 
Quindi
1/a
t 
a
t 
6
a
6
a
4
4
s( t )  u ( t ) 


 1,63C
6
6 2,45
Anita Calcatelli
a
a
a
6
t
s(t) = 1,6 °C
2013 -2014:Formazione&Metrologia
confronto
Anita Calcatelli
Distrib.
u(t)/°C
normale
0,7
rettangolare
2,3
triangolare
1,6
normale
2,0
Da 22 misure
Conoscendo
solo gli
estremi
2013 -2014:Formazione&Metrologia
Esempio:
Coefficiente di dilatazione termica lineare del rame
puro a 20 °C =16,52 x 10-6 °C-1 e il suo errore non
dovrebbe eccedere 0,40 x 10-6 °C-1
Perciò si può supporre che C può cadere con eguale
probabilità in qualunque punto dell’intervallo compreso
tra 16,12 x 10-6 °C-1 e 16,92 x 10-6 °C-1
La varianza di questa distribuzione
rettangolare simmetrica di valori possibili ,
di ampiezza 0,40 x 10-6 °C-1 è:
u 2 ( 20 )  (0,40 x10 6 ) 2 C 2 / 3  53,3 x10 15 C 2 )
E l’incertezza :
u ( 20 )  0,40 x106C 1 / 3  0,40 x106C 1 / 1,73  0,23 x106C 1
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Specifiche del costruttore
Voltmetro digitale
“accuratezza” data dal costruttore:
u’ = 14 x 10-6 x lettura + 2 x10-6 x campo, nella
scala da 1V e tra uno e due anni dalla sua
taratura.
Lo si usa 20 mesi dopo la taratura.
Si eseguono misurazioni ripetute da cui si ricava un
valore media (V) nella scala da 1 V
E si ha (V) = 0,928 571, con scarto tipo
sperimentale della media u[(V)] =12 V
Anita Calcatelli
Comp
tipo A
2013 -2014:Formazione&Metrologia
Come utilizzare le specifiche del costruttore?
L’accuratezza dichiarata si può pensare che
rappresenti i limiti simmetrici di una correzione
additiva V con (V) nulla e probabilità di giacere in
qualunque punto interno ai limiti di una distribuzione
u’ = 14 x 10-6 x lettura + 2 x10-6 x campo
a= [(14 x 10-6)x(0,928 571) + 2 x 10-6 x 1] V= 15 V
(V) = 0,0 V
Normale tra due estremi
Rettangolare
15
u(V)= 0,5 x 15 V=7,5 V
u V  
 8.68V
3
V = (V) + V= (0,928571 +0) V
uc(V) sarà una combinazione delle due componenti,
quella di tipo A dovuta alle letture ripetute e quella
Anita Calcatelli
2013 -2014:Formazione&Metrologia
di tipo B dovuta alle specifiche.
Componente di tipo A = u[m(V)] =12 mV
u2(V)=
u(V)=
Con distribuzione rettangolare della
componente B
u V  
u2(V)=
15
 8.68V
3
Con distribuzione normale della
componente B
u(V)=
u(DV)= 0,5 x 15 mV=7,5 mV
Anita Calcatelli
2013 -2014:Formazione&Metrologia
In sintesi
La valutazione di una incertezza di categoria
B è ottenuta da una densità di probabilità
ipotizzata in base al grado di credenza nel
verificarsi di un evento.
Entrambe le metodiche (valutazione di tipo
A e di tipo B) implicano interpretazioni della
probabilità universalmente riconosciute.
Anita Calcatelli
2013 -2014:Formazione&Metrologia
Fine parte 1
Anita Calcatelli
2013 -2014:Formazione&Metrologia