AA. 2009-2010
PSICOMETRIA
E ANALISI DEI DATI
c. Problemi di misurazione
RICCARDO LUCCIO
Dipartimento di Psicologia “G. Kanizsa”
Università di Trieste
Individuazione della scala di misura
1.
2.
3.
4.
5.
Si conduce una ricerca sui tempi di reazione di soggetti sottoposti
a diversi livelli di stress. A quale livello di misura ci si muove e
perché?
Si conduce una ricerca sulle preferenze dimostrate dagli alunni di
una classe per i compagni. A quale livello di misura ci si muove e
perché?
Si conduce una ricerca sulle percezione della chiarezza di figure
poste su sfondi di diverso colore. A quale livello di misura ci si
muove e perché?
Si conduce una ricerca sull’influenza della professione sullo stato
civile. A quale livello di misura ci si muove e perché?
Si conduce una ricerca sull’intelligenza misurata come QI. A
quale livello di misura ci si muove e perché?
Individuazione della scala di misura
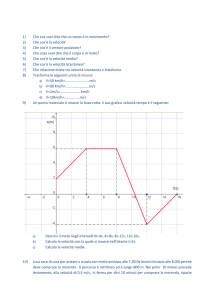
6. Si conduce una ricerca sulla percezione della velocità di movimento
di un mobile sullo schermo di un calcolatore. A quale livello di
misura ci si muove e perché?
7. Si conduce una ricerca sull’apprendimento di un brano di testo in
termini di numero di errori nella rievocazione. A quale livello di
misura ci si muove e perché?
8. Si conduce una ricerca sull’efficacia della cartellonistica
antiinfortunistica, misurata in termini di decremento degli
infortuni sul lavoro. A quale livello di misura ci si muove e
perché?
9. Si conduce una ricerca sull’influenza del sesso sulla scelta di giochi
competitivi o collaborativi nei bambini. A quale livello di misura
ci si muove e perché?
Rappresentazione di dati
Su una scala a nove punti
sono state trovate queste
frequenze di risposta.
Trovare:
1° e 3° quartile;
Mediana;
7° decile.
punti frequenze
1
11
2
14
3
15
4
22
5
44
6
41
7
23
8
4
9
1
Ripasso di algebra lineare
Posto che i dati precedenti fossero stati trovati su scala di intervalli,
calcola media e varianza delle frequenze con l’algebra lineare.
Fai il prodotto esterno del vettore dei dati e trova l’inversa di un
minore 3×3 della matrice così trovata.
Trova gli autovalori di questa matrice.
Verifica se questa matrice può essere l’inversa di quella.
"2 1 !2%
$
'
$ 3 1 !4'
$#1 !4 1 '&
Ripasso di calcolo combinatorio
1.
2.
Lily, studentessa di psicometria, civetta con 7 compagni di
corso, e per farli ingelosire esce sempre con due di loro insieme.
Dei compagni, 3 hanno i capelli rossi, 2 sono biondi e 2 mori.
Poiché Lily sceglie sempre coppie di accompagnatori con
capelli di colore diverso, per quante sere diverse ha compagnia
assicurata?
La piccola Cleofe Luponi festeggia il compleanno con 5
compagni di classe, tra cui i gemelli Pasztor. Per la torta,
siedono a un tavolo rotondo, e Cleofe evita di avere vicino uno
dei gemelli, che le danno sempre dei terribili pizzicotti. In
quanti modi potrà disporsi con i suoi amici?
Punto campione
1.
2.
A una gara partecipano 3 atleti della nazionale neo-zelandese e 4 della Libertas
Pischianzi, 2 neozelandesi sono biondi, il terzo ha i capelli rossi; 3atleti di
Pischianzi sono bruni e il terzo ha i capelli rossi. Utilizzando il metodo del
punto campione determinare la probabilità che:
1. Tra i primi tre ve ne siano 2 biondi;
2. Il primo e l’ultimo abbiano i capelli dello stesso colore;
3. Il quarto e il sesto appartengano alla stessa squadra
Agli atleti della gara precedente sono assegnati dei numeri, da 1 a 3 neri per i
neozelandesi, da 1 a 4 rossi per i pischianzini. Si formano delle coppie a caso,
indipendentemente dal colore dei numeri. Determinare la probabilità che si
può avere per ogni possibile somma di coppia di numeri, e costruire
l’istogramma.
Valore atteso
1.
2.
3.
In una ditta ci sono 7 impiegati di 4a categoria, uno di, un dirigente. Lo
stipendio lordo annuo del dirigente è 52.00 €, degli impiegati di 4a è un terzo,
l’impiegato di 7a guadagna una volta e mezzo quelli di quarta. Calcolare nel
modo più semplice possibile il valore atteso.
Dopo 5 anni questi stipendi sono aumentati del 20%. Calcolare nel modo più
semplice possibile il valore atteso.
Si calcolino anche le relative varianze.
Evidentemente il tutto va fatto con l’algebra lineare!
Test binomiale
1.
Il Foglieti, dentista tecnicamente modesto, estrae di solito con la stessa
probabilità i denti cariati quanto quelli che stanno alla loro destra e alla loro
sinistra. Ultimamente si è dato al bere, e delle ultime 12 estrazioni che ha fatto
solo 3 hanno riguardato denti cariati, mentre 9 hanno riguardato denti sani. Si
può ritenere che le sue capacità siano state danneggiate dall’alcool? (Enunciare
l’ipotesi nulla e l’ipotesi sostantiva, fissare α, calcolare la probabilità e
prendere la decisione statistica).
2.
Qual è il valore atteso di questi 12 eventi? E la varianza?