Calcolo delle probabilità
(riassunto veloce)
Laboratorio di Bioinformatica
Corso A
aa 2005-2006
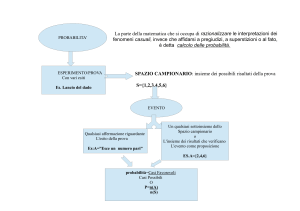
Teoria assiomatica della probabilità
• S = spazio campionario = insieme di tutti i
possibili esiti di un esperimento
• evento elementare = un qualsiasi
elemento di S
• evento = un qualunque sottoinsieme E
dello spazio campionario S
• si dice che l’evento E si è realizzato se il
risultato dell’esperimento è un elemento di
E
Operazioni con gli eventi
• somma logica (o unione):
A∪ B
• prodotto logico (o intersezione):
A∩ B
• evento contrario il complementare di A
rispetto a S:
A
• A e B si dicono incompatibili (o
mutuamente esclusivi) se
A∩ B = ∅
Definizione formale (assiomatica)
della probabilità
• Sia S uno spazio campionario
• Sia P una funzione a valori reali definita
sui sottoinsiemi di S (eventi) a valori reali
tale che:
– 0 ≤ P(E) ≤ 1
– P(S)=1
– Per ogni coppia di eventi E1 ed E2
incompatibili si ha
P(E1 U E2) = P(E1)+P(E2)
P(E) si dice probabilità dell’evento E
Se S contiene infiniti elementi
La terza condizione diventa
• Per successioni di eventi E1, E2, … a due a due
incompatibili, cioè t. c. Ei ∩ Ej = Ø se i ≠ j si ha
P U Ei = ∑ P(Ei )
i =1 i =1
∞
∞
Relazioni elementari
• Probabilità del complementare
()
P E = 1 − P (E )
P(∅ ) = 0
• Monotonia
E2 ⊂ E1
P( E1 ) ≥ P( E2 )
• Unione e intersezione
P(E1UE2) = P(E1) + P (E2) - P(E1∩E2)
La definizione classica
• Se S è uno spazio campionario formato da
eventi elementari equiprobabili la probabilità
di un evento E è data da
P(E) = # elementi di E / # elementi di S
= # casi favorevoli / # casi possibili
Esercizio: compleanni
• Calcoliamo la probabilità che scegliendo a
caso n persone almeno due di esse
festeggino il compleanno lo stesso giorno.
• Ipotesi operativa: i bambini nascono con la
stessa probabilità in ognuno dei 365 giorni
dell’anno.
• A = {almeno due delle n persone
festeggiano il compleanno lo stesso giorno}
Esercizio compleanni
• Calcoliamo la probabilità di A = { tra gli n
compleanni non ve ne sono due uguali}
• # eventi possibili = # n-uple formate scegliendo
tra i 365 giorni = 365n
• # eventi favorevoli a A = # n-uple formate
scegliendo tra i 365 giorni senza ripetizioni =
365 * 364 * …* (365 – n +1)
365 ⋅ 364 ⋅ K ⋅ (365 − n + 1)
364
365 − n + 1
PA =
= 1⋅
⋅L ⋅
n
365
365
365
()
Proviamo alcuni n
compleanni.xls - Foglio1!A1
Fissiamo il compleanno
• Vogliamo calcolare la probabilità dell’evento B =
{tra n persone almeno una ha il mio stesso
compleanno}
• Calcoliamo la probabilità del complementare
364
364
PB =
=
n
365
365
n
364
P (B ) = 1 −
365
()
compleanni.xls - Foglio3!A1
n
n
Calcolo delle probabilità
(probabilità condizionata)
Laboratorio di Bioinformatica
Corso A
aa 2005-2006
Probabilità condizionata
• La probabilità di un evento può variare
quando si aggiungono informazioni, ad
esempio il fatto che un altro evento si è
verificato.
Esempio: lancio di un dado
• Prima di lanciare un dado, la probabilità di
ottenere il numero 5 è 1/6.
• Supponiamo che dopo il lancio del dado una
persona mi riferisca che il numero uscito è
dispari.
• La probabilità, per effetto della nuova
informazione è salita a 1/3.
• L’informazione acquisita mi ha portato a
“rinnovare” lo spazio campionario dall’iniziale
S = {1, 2, 3, 4, 5, 6} a S' = {1, 3, 5} .
Probabilità condizionata
• Si definisce probabilità di un evento A
condizionata (o subordinata) all'evento
B, e s'indica P( A | B ), la probabilità del
verificarsi di A nell'ipotesi che B si sia
verificato.
Probabilità condizionata
S
A
B
A∩B
Dobbiamo restringere a B lo spazio campionario e
ridefinire su B la probabilità. La sola parte di A
significativa resta A ∩ B.
P( A ∩ B)
P( A | B) =
P( B)
In altre parole
• La formula precedente si può leggere
come
P( A ∩ B) = P( A | B) ⋅ P( B)
P( A ∩ B ) = P( B | A) ⋅ P( A)
Teorema della probabilità
composta
Eventi indipendenti
• Da un mazzo di carte da briscola si estrae una carta.
La probabilità che sia fiori è 10/40 = 1/4.
• Se so che la carta estratta è una figura, la probabilità
che si tratti di una carta di fiori rimane 3/12=1/4.
A = "esce una carta di fiori"
F = "esce una figura"
p(A) = 1/4 = p(A|F)
• Il verificarsi di F non modifica la probabilità che A si
verifichi.
• Si dice allora che i due eventi sono indipendenti
Eventi indipendenti
Due eventi A e B si dicono (stocasticamente)
indipendenti quando la conoscenza del
verificarsi di uno dei due non dà alcuna
informazione sul verificarsi dell’altro.
Due eventi A e B si dicono (stocasticamente)
indipendenti quando si verifica una delle due
condizioni equivalenti
P ( A) = P ( A | B )
o
P ( B) = P ( B | A)
Eventi indipendenti
(ancora una definizione)
Due eventi A e B si dicono
(stocasticamente) indipendenti quando
P( A ∩ B) = P( A) ⋅ P( B)
ATTENZIONE!
• Non confondere eventi indipendenti con
eventi incompatibili.
• Se due eventi sono incompatibili il
verificarsi di uno dei due esclude il
verificarsi dell’altro quindi non sono
indipendenti. Ad esempio
• A= esce testa
• B= esce croce
Teorema di Bayes
• Sia { A, B } una partizione dell’insieme
campionario, cioè una coppia di eventi tali che
A∪ B = S
e
A∩ B = ∅
• Supponiamo di conoscere P(A)>0 e P(B)>0
• Sia C un terzo evento del quale si conoscono
P(C | A) e P(C | B)
Un disegno
C
A
B
Teorema di Bayes
• Se si verifica C, qual è la probabilità che si sia
verificato A?
P ( A ∩ C ) P(C | A) ⋅ P( A)
P( A | C ) =
=
P (C )
P(C )
P(C | A) ⋅ P ( A)
=
P(C ∩ A) + P(C ∩ B)
P(C | A) ⋅ P( A)
=
P(C | A) ⋅ P( A) + P(C | B) ⋅ P( B)
Teorema di Bayes
Sia {E1, E2, …, En} una partizione si S, cioè una
collezione di eventi tali che
n
Ei ∩ E j = ∅ se i ≠ j e
UE
i
=S
i =1
Allora, se P(Ei)>0 per ogni i ed A è un evento con
P(A)>0 vale la formula
P ( E j | A) =
Effetto
P( A | E j ) ⋅ P( E j )
n
∑ P( A | E ) ⋅ P( E )
i
i =1
i
Cause