Politecnico di Milano - Academic Year 2010-2011
Statistica 086449
Docente: Alessandra Guglielmi
Esercitatore: Stefano Baraldo
Esercitazione 3
5 Aprile 2011
Esercizio 1. Diciamo che X ha distribuzione Gamma(α, λ), con α > 0, λ > 0,
se la sua densità ha la seguente forma:
fX (x) =
λα α−1 −λx
x
e
I(0,+∞) (x).
Γ(α)
dove Γ(α), per α > 0, è la funzione Gamma definita come
Z
+∞
tα−1 e−t dt.
Γ(α) =
0
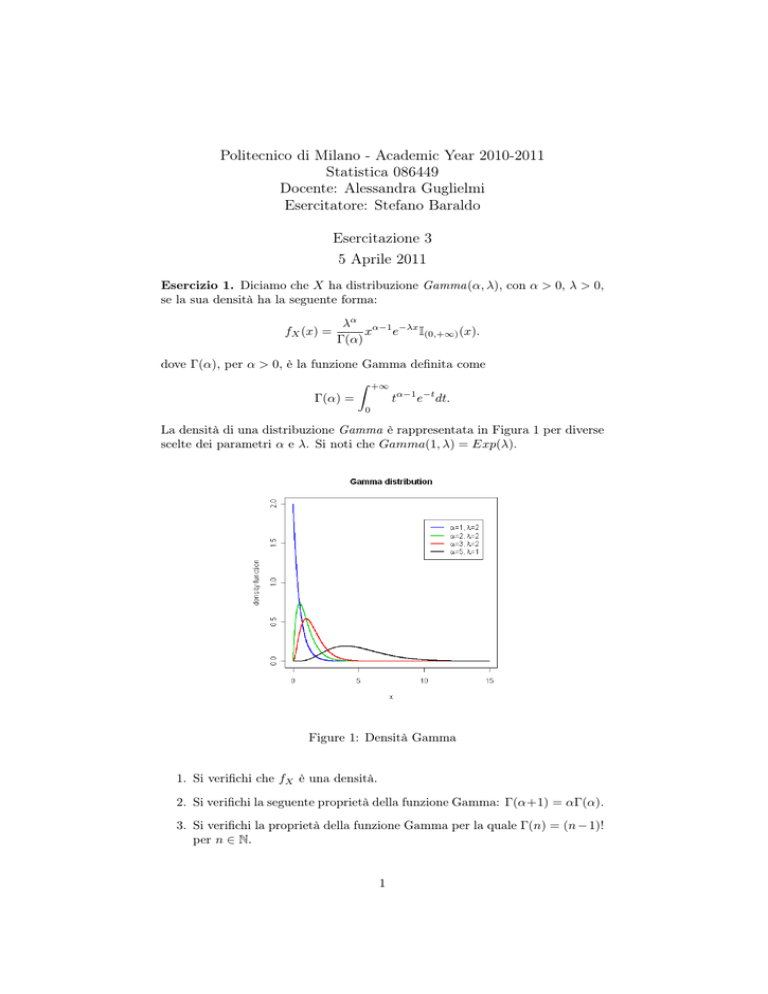
La densità di una distribuzione Gamma è rappresentata in Figura 1 per diverse
scelte dei parametri α e λ. Si noti che Gamma(1, λ) = Exp(λ).
Figure 1: Densità Gamma
1. Si verifichi che fX è una densità.
2. Si verifichi la seguente proprietà della funzione Gamma: Γ(α+1) = αΓ(α).
3. Si verifichi la proprietà della funzione Gamma per la quale Γ(n) = (n − 1)!
per n ∈ N.
1
4. Si verifichi che E[X] =
α
λ
e Var(X) =
α
λ2 .
Soluzione.
1. fX (x) è una densità perché è sempre non negativa e
Z
R +∞
+∞
fX (x)dx =
0
−∞
λα xα−1 e−λx dx
=1
R +∞
tα−1 e−t dt
0
grazie al cambio di variabile λx = t nell’integrale al numeratore. Si noti
che dx = dt/λ.
R +∞
R +∞
+∞
2. Γ(α + 1) = 0 tα e−t dt = 0 αtα−1 e−t dt − [tα e−t ]0 = αΓ(α).
R +∞
3. Γ(1) = 0 e−t dt = 1, e utilizzando la proprietà al punto 2 otteniamo
Γ(n) = (n − 1)Γ(n − 1) = (n − 1)(n − 2) × Γ(n − 2)
= (n − 1)(n − 2)(n − 3) · · · 2 · 1 Γ(1) = (n − 1)!
4. Poiché
R +∞
0
λα
α−1 −λx
e
dx
Γ(α) x
= 1, otteniamo che
R +∞
0
xα−1 e−λx dx =
Γ(α)
λα .
+∞
λα
λα α−1 −λx
x
e
dx =
Γ(α)
Γ(α)
0
α
λα Γ(α + 1)
= .
=
Γ(α) λα+1
λ
Z
E[X] =
Z
+∞
x(α+1)−1 e−λx dx
x
0
È anche possibile calcolare E[X] tramite integrazione per parti.
+∞
λα
λα α−1 −λx
x
e
dx =
E[X ] =
x
Γ(α)
Γ(α)
0
α
λ Γ(α + 2)
α(α + 1)
=
=
.
Γ(α) λα+2
λ2
2
Z
2
E otteniamo Var(X) = E[X 2 ] − E[X]2 =
Z
α(α+1)
λ2
+∞
x(α+2)−1 e−λx dx
0
−
α2
λ2
=
α
λ2
Esercizio 2. Stando alle statistiche riguardanti la Divisione di Pronto Soccorso
del Desert Samaritan Hospital di Mesa, AZ, si trova che, dalle 6 del pomeriggio,
il tempo (in ore) di ingresso di attesa per l’ingresso del terzo paziente segue una
distribuzione Gamma di parametri α = 3 e λ = 6.9.
1. Si calcoli la funzione di ripartizione.
Si valuti la probabilità che, a partire dalle 6 del pomeriggio, il terzo paziente
arrivi
2. prima delle 7;
3. tra le 6:15 e le 6:30.
2
Soluzione. Sia X il tempo di attesa (in ore) fino all’entrata del terzo paziente:
X ∼ Γ(3, 6.9); quindi la sua densità è data da
f (x) =
6.93 3−1 −6.9x
x e
I(0,+∞) (x).
Γ(3)
1. Se α ∈ N, α = 3 in questo caso, la funzione di ripartizione può essere
calcolata tramite integrazioni per parti successive come
FX (x) = 1 −
α−1
X
k=0
e−λx (λx)k
I(0,+∞) (x).
k!
In questo caso otteniamo
FX (x) = 1 −
3−1 −6.9x
X
e
(6.9x)k
k!
k=0
I(0,+∞) (x)
2. P(0 < X < 1) = FX (1) − FX (0) = FX (1) = 0.968048
3. P(1/4 < X < 1/2) = FX (1/2) − FX (1/4) = 0.420415
Esercizio 3. Durante la 30esima settimana di gravidanza, il tasso di sedimentazione X segue una legge Γ(5, 0.1).
1. Si calcolino la densità e la funzione di ripartizione di X;
2. Si calcoli la probabilità che durante la 30esima settimana di gravidanza il
tasso di sedimentazione sia almeno pari a 60;
3. Si calcoli la probabilità che durante la 30esima settimana di gravidanza il
tasso di sedimentazione sia compreso tra 40 and 50.
3
Soluzione.
1. La densità è
fX (x) =
0.15 4 −0.1x
x e
I(0,+∞) (x);
Γ(5)
la funzione di ripartizione è
FX (x) = 1 −
5−1 −0.1x
X
e
(0.1x)j
j!
j=0
I(0,+∞) (x).
2. P(X ≥ 60) = 1 − FX (60) = 0.28506
3. P(40 ≤ X ≤ 50) = FX (50) − FX (40) = 0.188343
Esercizio 4. Diciamo che X ha distribuzione Weibull di parametri α > 0
(parametro di scala) e β > 0 (parametro di forma) se la sua densità ha la
seguente forma:
β
fX (x) = αβxβ−1 e−αx I(0,+∞) (x).
La densità di una variabile Weibull è rappresentata nella Figura 2, per diverse
scelte dei parametri α e β. La variabile aleatoria Weibull ha media E[X] =
Figure 2: Densità Weibull
2
1
2
α− β Γ 1 + β1 e varianza Var(X) = α− β Γ 1 + β2 − Γ 1 + β1
1. Si calcoli la funzione di ripartizione FX ;
2. Si mostri che se X ∼ exp(λ), allora Y = X 1/γ ha legge W eibull(λ, γ),
dove γ > 0.
Soluzione.
4
1. Per X ∼ W eibull(α, β) abbiamo
β
FX (x) = 1 − e−αx I(0,+∞) (x)
2. Utilizziamo il teorema di trasformazione di variabili aleatorie:
y = g(x) = x1/α ⇒ x = g −1 (y) = y α ,
quindi
fY (y) = fX (g
−1
−1 dg (y) = λγy γ−1 e−λyγ
(y)) dy che è la densità di una variabile aleatoria Weibull(λ, γ).
Esercizio 5. Si supponga che il tempo di vita di un componente elettronico
segua una distribuzione Weibull di parametri α = 2 e β = 1/9, col tempo
espresso in anni.
1. Si disegni il grafico della densità e si calcoli la funzione di ripartizione del
tempo di vita del componente;
2. si calcoli la probabilità che il componente duri almeno 6 mesi;
3. si calcoli la probabilità che il tempo di vita di un componente sia compreso
tra 6 mesi e un anno.
Soluzione.
1. La densità è rappresentata in Figura 3 e la funzione di ripartizione è
FX (x) = 1 − e−2x
1/9
2. P(X ≥ 0.5) = 1 − FX (0.5) = e−2(0.5)
1/9
I(0,+∞) (x)
= 0.1569623
1/9
3. P(0.5 ≤ X ≤ 1) = FX (1) − FX (0.5) = e−2(0.5)
− e−2 = 0.02162705
Esercizio 6. Tema d’esame del 17/11/2008
Sia X una variabile aleatoria assolutamente continua uniforme sull’intervallo
(0, 1).
1. Verificare che Y = − λ1 log(X), dove λ è un parametro positivo e log indica
il logaritmo naturale, ha distribuzione Exp(λ).
Si supponga ora che il tempo di vita di una ventola di raffreddamento
√ di un
computer, espressa in migliaia di ore, sia una variabile aleatoria U = Y , con
Y ∼ Exp(λ) e λ = 0.03.
2. Calcolare esplicitamente la funzione di ripartizione di U , verificare che corrisponde ad una distribuzione assolutamente continua e ricavare la densità
di U .
3. Calcolare la probabilità che la ventola duri almeno 2500 ore.
Soluzione.
5
Figure 3
1. Se X ∼ U ([0, 1]), Y = − λ1 log(X) ≥ 0 q.c.. Quindi, se y ≤ 0, FY (y) = 0,
mentre, se y > 0,
1
FY (y) = P(Y ≤ y) = P − log(X) ≤ y = P(log(X) ≥ −λy)
λ
= P(X ≥ e−λy ) = 1 − FX (e−λy ) = 1 − e−λy .
Dunque la funzione di ripartizione di Y coincide con quella di una esponenziale di parametro λ.
2. Se u ≤ 0, FU (u) = 0; se, invece, u > 0:
√
2
FU (u) = P( Y ≤ u) = P(Y ≤ u2 ) = FY (u2 ) = 1 − e−λu .
La funzione di ripartizione FU è differenziabile per ogni u 6= 0 e quindi la
sua densità siottiene nel seguente modo:
2
fU (u) = FU0 (u) = 2λue−λu I(0,+∞) (x).
U ha distribuzione Weibull(2, λ).
3. Si tratta di calcolare
2
P(U ≥ 2.5) = 1 − FU (2.5) = e−0.03×(2.5) = e−0.1875 ∼
= 0.8290.
Esercizio 7. Sia X ∼ Exp(λ); si calcoli la legge della variabile aleatoria Y =
(2X/λ)1/2 .
Soluzione. Per il teorema di trasformazione di variabili aleatorie si ottiene
facilmente che
2 2
fY (y) = λ2 ye−λ y /2
che è una distribuzione di Rayleigh di parametro λ2 .
6
Esercizio 8. Sia X il numero di corsi ai quali uno studente universitario scelto
a caso risulta iscritto. La distribuzione di probabilità di X è la seguente
x
p (x)
1
0.02
2
0.03
3
0.09
4
0.25
5
0.40
6
0.16
7
0.05
1. Determinare la probabilità che lo studente sia iscritto a 4 corsi.
2. Determinare la probabilità che lo studente sia iscritto a non più di 3 corsi.
3. Determinare la probabilità che sia iscritto a più di 3 corsi e meno di 6.
4. Determinare la funzione di ripartizione di X e disegnarne il grafico.
5. Calcolare il valore atteso e la deviazione standard del numero di corsi.
Soluzione.
1. P(X = 4) = p(4) = 0.25
2. P(X ≤ 3) = p(1) + p(2) + p(3) = 0.14
3. P(3 < X < 6) = p(4) + p(5) = 0.65
4.
0
0.02
0.05
0.14
F (x) =
0.39
0.79
0.95
1
se x < 1
se 1 ≤ x < 2
se 2 ≤ x < 3
se 3 ≤ x < 4
se 4 ≤ x < 5
se 5 ≤ x < 6
se 6 ≤ x < 7
se x ≥ 7
Pn
Pn
2
5. E[X] =
Xi p(i) = 4.66; E[X 2 ] =
i=1
i=1 Xi p(i) = 23.16, da cui
q
p
2
V ar(X) = E[X 2 ] − E[X] = 1.20
Esercizio 9. Consideriamo le seguenti funzioni F e G:
0,
x<0
1
,
0
≤
x<1
2
F (x) =
3
,
1
≤
x<4
4
1,
x≥4
0,
x<0
1
,
0
≤
x≤1
2
G (x) =
3
,
1
<
x<4
4
1,
x≥4
1. Quale delle due è una funzione di ripartizione? Disegnarne il grafico.
2. Si determini la funzione di probabilità associata ad F . Inoltre si calcoli
P(X < 4); P(X ≤ 3) e P(X = 1).
3. Calcolare il valore atteso di X.
7
Soluzione.
1. La funzione F è una funzione di ripartizione (infatti è non decrescente,
continua a destra, e tale che limx→−∞ F (x) = 0 e limx→+∞ F (x) = 1). La
funzione G invece non è una funzione di ripartizione perchè non è continua
a destra.
2. p(0) = 1/2, p(1) = 1/4, p(2) = 0, p(3) = 0, p(4) = 1/4.
P(X < 4) = p(0) + p(1) = 3/4;
P(X ≤ 3) = F (3) = p(0) + p(1) = 3/4;
P(X = 1) = p(1) = 1/4.
3. E[X] = 5/4
Esercizio 10. Determinare la costante c ∈ R tale per cui la seguente funzione
è una densità discreta:
p (x) = c
x
, per x = 0, 1, . . . , 120.
120
Calcolarne il valore atteso.
Soluzione. Affinchè la funzione scritta sopra sia una densità discreta occorre
che tutti i pesi siano
non-negativi
e che sommino
ad uno, e quindi deve essere
P120
1
2
1
c > 0 e 1 = c 120
121
×
60
,
da
cui
c = 121
i
=
c
.
i=0 120
P120
Pn
120×121×241
2 1
2 1
2
=
80.333
perchè i=0 i2 =
E[X] = 121 120
i
=
i=0
121 120
6
n(n+1)(2n+1)
.
6
Esercizio 11. Si consideri la variabile aleatoria discreta X con legge data dalla
funzione di ripartizione
0
x<0
1/3 0 ≤ x < 1
F (x) =
5/6 1 ≤ x < 3
1
x≥3
Disegnare la funzione di
√ ripartizione di X. Calcolare la funzione di probabilità
e i valori attesi di X e X.
√
Soluzione. p(0) = 1/3, p(1) = 1/2, p(3) = 1/6; E[X] = 1; E[ X] = 0.7887
8












