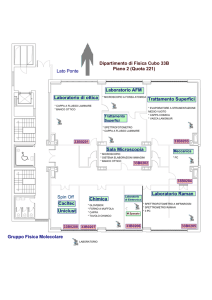
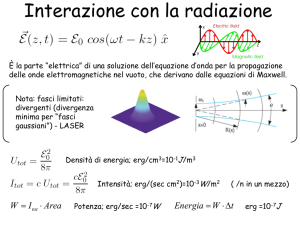
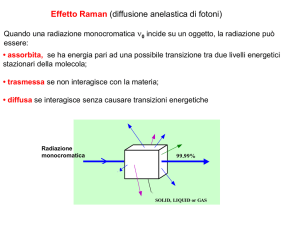
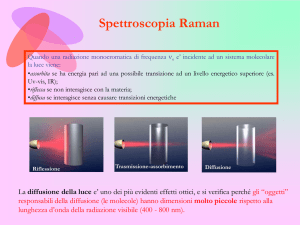
Spettroscopia Raman.
Introduzione
Descrizione quantistica di un cristallo. Esempio: Silicio
http://en.wikipedia.org/wiki/File:Silico
n-unit-cell-3D-balls.png
http://www.exploreroots.com/a3.htm
l
Descrizione quantistica di un cristallo.
Approssimazione di Born-Oppenheimer
L'approssimazione BO si basa sul fatto che la massa degli elettroni è molto minore di
quella dei nuclei.
Massa dell'elettrone: 9.108 10-31 kg
Massa del protone: 1.673 10-27 kg
Massa del neutrone: 1.675 10-27 kg
Dunque l'energia cinetica degli ioni (nuclei più ellettroni interni) risulta molto minore di
quella degli elettroni di valenza.
Si risolve allora il problema della determinazione dei livelli energetici elettronici,
considerando gli ioni fissi nella loro posizione di equilibrio.
In secondo luogo, si risolve il problema del moto vibrazionale degli ioni che risentono del
moto medio degli elettroni.
Il moto vibrazionale degli ioni (onde meccaniche) è quantizzato (analogamente alla
quantizzazione delle onde elettromagnetiche.)
Un quanto di vibrazione si dice fonone.
Infine si prende in considerazione l'influenza del moto degli ioni sugli elettroni:
l'interazione elettrone-fonone
Stati elettronici e vibrazionali
Determinati dal vettore d'onda k
L1= N 1 a 1,
L2= N 2 a 2,
L3 =N 3 a3
N =N1 N 2 N 3
m1
m2
m3
k = b 1+
b2 +
b3
N1
N2
N3
m1, m2, m3 interi
Stati elettronici e vibrazionali
k' e k indicano lo stesso stato quantico se differiscono di
un vettore del reticolo reciproco.
k
b2
K
k'
b1
Tutti i possibili vettori d'onda k degli elettroni (dei
fononi) sono contenuti in una sola cella primitiva del
reticolo reciproco
Stati elettronici. Silicio: prima zona di Brillouin e bande
E j = E j (k) j -esima banda di energia
Bandgap indiretto
Bandgap (semiconduttori, isolanti)
Dato che il numero di celle primitive (e di livelli
energetici per banda) è N e gli stati per ogni livello
energetico sono 2 (grado di libertà di spin) l'esistenza di
un bandgap richiede che il numero di elettroni per cella
primitiva sia pari.
Metalli
Bande parzialmente riempite
Il livello di energia che separa bande piene e vuote è
detto energia di Fermi EF
semiconduttore
semiconduttore
En (k)=E F
è il ramo della superficie di Fermi dell' n-esima
banda
semimetallo
http://en.wikipedia.org/wiki/Semimeta
l
Diamond: Electronic Properties and Applications: Electronic Properties and
Applications Lawrence S. Pan, Don R. Kania Springer, 31/dic/1994
Stati fononici.
E=ℏ ω∼0.1 eV
Stati fononici. Reticolo tridimensionale con base
Curve di dispersione
fononica, silicio
Fundamentals of
Semiconductors: Physics
and Materials Properties
Peter YU, Manuel
Cardona, Springer
Per ogni valore di q nella FBZ ci sono 3p modi normali, 3 modi acustici e 3p-3 modi
ottici, con p numero degli atomi della base.
ωi (q)
per ogni ramo è una funzione periodica con la periodicità del reticolo reciproco
I modi sono quantizzati e a ognuno è assegnato un insieme discreto di energie:
(
nq ,i +
1
ℏ ωi (q) nq ,i numero di fononi
2
)
I fononi seguono la staistica di Bose-Einstein:
1
nq ,i=
e
ℏ ω i (q)
kT
−1
Regole mnemoniche
14
3×10
ν (Hz) =
λ ( μm )
4
10
ν̃ (cm ) =
λ ( μm )
−1
E (eV) =
1.24
λ ( μm )
Scattering Raman
Un fotone di luce visibile può essere diffuso dal reticolo con
l'emissione o l'assorbimento di un fonone. Questo
“scattering” anelastico è molto meno intenso dello
scattering elastico (Rayleigh). Quindi si osserva
usualmente utilizzando una sorgente laser.
Se i fononi interessati sono acustici si parla di Scattering
Brilloun, se sono ottici , si parla di Scattering Raman
ℏ ω' =ℏ ω±ℏ ω i(q )
ℏ k ' =ℏ k±ℏ q +ℏ K
k ' ,k
conservazione dell'energia
conservazione del momento cristallino
Sono i vettori d'onda del fotone nel mezzo,
k =n k 0
k'
k'
Processo
antiStokes
q
k
q
Processo Stokes
k
q
q
Sezione d'urto di scattering
Scattering of Light by
Crystals
William Hayes, Rodney
Loudon, Dover
Sezione d'urto differenziale e spettrale
I0
dσ
=energia diffusa per unità di tempo, angolo solido e frequenza
d Ωd ω
Relazione tra sezioni d'urto di scattering Stokes e anti-Stokes
nq ,i
[
dσ
dΩd ω
]
Stokes
=(nq ,i +1)
[
dσ
dΩd ω
]
antiStokes
ℏ ω' =ℏ ω±ℏ ω i(q )
ℏ k ' =ℏ k±ℏ q +ℏ K
Luce visibile
ω ≈5×1014 Hz
2π
Vettore d'onda del fotone incidente
k=
Intervallo dei “Raman shift” in frequenza:
“Raman shift”
“Brillouin shift”
1
ν̃ = λ =17000 cm −1
λ =600 nm
2π
n=1.6×10 5 cm −1
λ
3×1011<
1 1
ν̃ −ν̃ '= −
λ λ'
ωi (q )
<1014 Hz
2π
10-3000 cm-1
1 cm-1
Dunque nella maggior parte degli esperimenti:
ωi (q)≪ω
k≈k '∼105 cm −1
1/1000 della zona di Brillouin
K=0
k'
Processo Stokes
k
q
q
k'
q
q
k
q=2k sin θ
2
q≈0
Esempio, spettro Raman del Si
q≈0
1 Bohr = 0.53 Å
10.34 Bohr = 5.47 Å
http://www2.warwick.ac.uk/services/rss/business/analyticalguide/raman
Esempio, spettro Raman del diamante monocristallino
6.7468 Bohr = 3.57 Å
Raman spectroscopy of diamond and doped diamond
Steven Prawer and Robert J. Nemanich
Phil. Trans. R. Soc. Lond. A 2004 362, 2537-2565
Esempio, spettro Raman dela grafite
http://graphitecrystals.com/stm.htm
l
Difetti, rilassamento della regola q=0
Materiale policristallino: dimensione
lineare dei grani d
Δ q≈
2π
d
Al diminuire delle dimensioni dei
grani lo spettro Raman riflette la
densità degli stati fononici
Spettro Raman della grafite cristallina
Picco G e secondo ordine G*
Picco D (disordered) dovuto a difetti del reticolo e seconda armonica D*
Il picco D coinvolge fononi al bordo K della FBZ ed è legato alle dimensioni dei
grani d
I ( D) A (λ )
=
I (G)
d
A (515 nm )=44 Å
Dispersione del picco D della grafite
Allargamento della riga del diamante in funzione della dimensione dei grani
Raman spectroscopy of diamond and doped diamond
Steven Prawer and Robert J. Nemanich
Phil. Trans. R. Soc. Lond. A 2004 362, 2537-2565
doi: 10.1098/rsta.2004.1451
Spettro Raman di diamante sintetico policristallino
Dipendenza dello spettro del diamante dalla lunghezza d'onda (energia del fotone) di
eccitazione
Resonant Raman scattering of amorphous carbon and
polycrystalline diamond films
J. Wagner, M. Ramsteiner, Ch. Wild, and P. Koidl
Phys. Rev. B 40, 1817 – Published 15 July 1989
Resonance effects in Raman scattering from
polycrystalline diamond films
J. Wagner, C. Wild, and P. Koidl
Citation: Applied Physics Letters 59, 779 (1991);
doi: 10.1063/1.105340
Δ ν̃ = Δ λ2
λ
Dipendenza del Raman shift dalla pressione
Δ ω =−γ Δ V
ω
V
International Journal of Spectroscopy
Volume 2012 (2012), Article ID 617528, 16 pages
http://dx.doi.org/10.1155/2012/617528
Review Article
Raman Spectroscopy at High Pressures
Alexander F. Goncharov
V volume del cristallo
Δ ω =2.7−2.9 cm −1 /GPa
ΔP
Luminescenza Si-V a 738 nm
Spettro di assorbimento del diamante