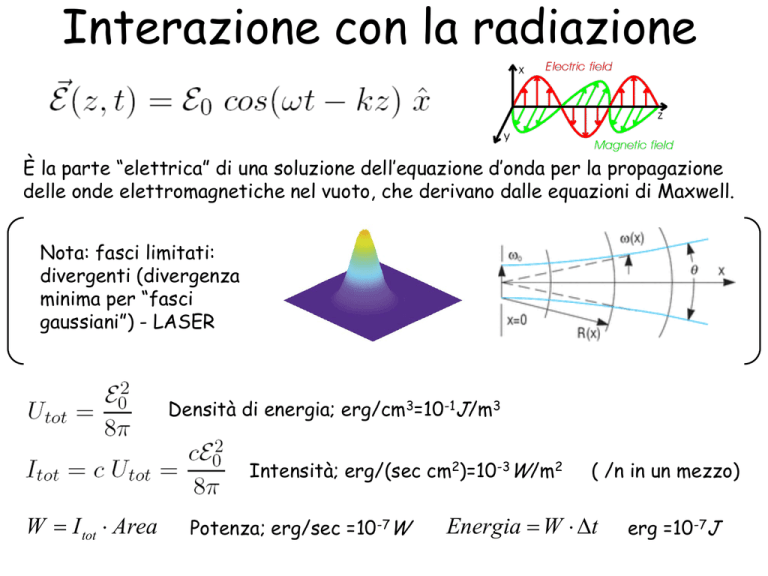
Interazione con la radiazione
È la parte “elettrica” di una soluzione dell’equazione d’onda per la propagazione
delle onde elettromagnetiche nel vuoto, che derivano dalle equazioni di Maxwell.
Nota: fasci limitati:
divergenti (divergenza
minima per “fasci
gaussiani”) - LASER
Densità di energia; erg/cm3=10-1J/m3
Intensità; erg/(sec cm2)=10-3W/m2
W = I tot ⋅ Area
Potenza; erg/sec =10-7W
( /n in un mezzo)
Energia = W ⋅ ∆t
erg =10-7J
Ripasso
Conosciamo le soluzioni dell’equazione di Schrödinger di base:
Rappresentazione nello spazio degli autostati di H0:
Considero una perturbazione:
Riscrivo l’equazione di Schrödinger completa dipendente dal
tempo nello spazio degli autostati di H0:
(3.2.1)
Teoria delle perturbazioni
dipendente dal tempo:
(3.3.3)
Ordine 1:
(3.3.4)
Caso particolare:
perturbazione sinusoidale su un autostato
(3.3.1)
(3.3.2)
Regola d’oro di Fermi
Interazione con la radiazione
Campo elettrico
Se λ=2π/k >> dimensioni del sistema: approssimazione di dipolo:
I
δ (ω − ωk 0 ) (3.4.1)
Regola d’oro di Fermi
;
(3.4.3)
Absorption
Stimulated Spontaneous
Emission
Emission
Maxwell equation
(thermal equilibrium)
−
E1
kT
hν
−
n1 e
= E0 = e kT
−
n0
e kT
0
“Planck” Black
Body Radiation
Dipolo indotto da E
Lineare:
Non lineare:
Generazione di seconda armonica:
Raman (vibrazionale)
Una molecola non è ferma:
Consideriamo una frequenza
(di vibrazione) ω' :
Dipolo indotto
Generalizzazione: ω'
ωkn (frequenza di risonanza del sistema)
Example
From Cyrus Farokh Hirjibehedin Ph.D. Thesis
Alcune non-linearità: ordine 2
Consideriamo uno spettro non banale per f(t); per mantenere le cose semplici:
Il doppio integrale
sarà quindi dato da una somma di termini del tipo:
Sostituendo il risultato dell’integrale nell’espressione per
, considerando solo
I termini derivanti dall’espressione nel riquadro
, e con considerazioni simili a
quelle che portano alla regola d’oro di Fermi (e considerando solo termini non
trascurabili…) un contributo al secondo ordine alla probabilità di transizione dal
livello n al livello j è legato a:
(3.15.1)
Assorbimento a 2 fotoni:
ω1=ω2=ω
n
ω
ω
g
γ
ωnk+ ωkj = ωnk− ωjk= ωnj
Raman
ω2 = ωL (-)
ω1 = ωS (+)
(3.16.1)
(3.16.1)
Raman non risonante
Per W(x) ~ e Ei x, la probabilità per il Raman
diventa circa proporzionale a:
e 4 EL2 ES2, 0
(3.17.1)
(Questa semplificazione si trova in alcuni testi; ha una certa validità per
sistemi con pochi livelli molto ben separati, e lontano dalla risonanza)
Is/Ias=[(ν0-νvib)/ (ν0+νvib)]3exp(hνvib/kT)
F
F
Fluore
scence
Thermally activated
fluorescence
Electronic - vibrational spectroscopy
Coordinate elettroni
Coordinate nuclei
n
Funzione d’onda elettronica
Funzione d’onda (vibrazionale) nucleare
Born-Oppenheimer Approximation
Ψ
Ψ
φ
φ
Infrared vibrational spectroscopy
Coordinate elettroni
Funzione d’onda elettronica
Coordinate nuclei
Funzione d’onda (vibrazionale) nucleare
Il dipolo elettronico dipende dalla posizione dei nuclei:
L’elemento di matrice di dipolo vale:
0
Regole di selezione per funzioni d’onda nucleari ed elettroniche
0
Electronic transitions
1
L’elemento di matrice di dipolo vale:
1
1
Fattori
di Franck
Condon