11.9 Gli amplificatori distribuiti e l`amplificatore Raman

11.9 Gli amplificatori distribuiti e l’amplificatore
Raman
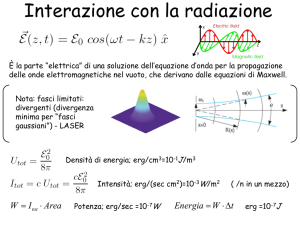
Abbiamo visto al paragrafo 11.3 che per piccoli segnali l’equazione di
guadagno dell’Amplificatore Ottico diventa
Ip
dIs
= "# sa N1Is + $# sa
N1Is
dz
I pump sat
dalla quale introducendo il nuovo parametro sintetico gedfa definito come
!
gedfa =
" a#N1
I pump sat
ottengo
!
!
dIs
= "# sa N1Is + gedfa IpIs
dz
Questa equazione fa “sistema” con l’equazione di attenuazione della
pompa
dIp
= "# pa N1Ip
dz
!
Queste due equazioni sono particolarmente adatte ad una trattazione
propagativa dell’AO, ovvero a descrivere fenomeni che avvengono con la
propagazione di “campi” all’interno delle fibre ottiche.
La seconda equazione rappresenta semplicemente l’attenuazione che
subisce la pompa mentre propaga. La prima equazione mi dice, al primo
termine del secondo membro, che l’intensità del segnale viene attenuata
con il processo classico di attenuazione in fibra (dove ad esempio Σ
abbiamo visto valere 5.5 10 "5 m "1) + un termine di “guadagno” che è
funzione dell’intensità di pompa Ip e di Is stessa (ovvero del processo
stimolato). Tutta la fisica dell’inversione di popolazione rimane
!
“nascosta” dentro
il coefficiente gedfa e la funzione di pompaggio viene
!
invece esplicitata dalla presenza
di!Ip .
Valutiamo gedfa. Per " a = 4.64 10#25 m 2 $ = 1 I pump sat = 5.4 10 7 W /m 2 ed un
drogaggio pari a 10 ppm!(cui corrispondono circa NT " N1 = 5.73 10 23 m#3 )
!
!
Comunicazioni Ottiche, Edizione gennaio 2010, Capitolo
11
!
ottengo:
gedfa
"#N1 4.64 10$255.73 10 23
m
=
=
% 4.92 10$9
7
I pump sat
5.4 10
W
Usando questo sistema di espressioni posso facilmente studiare
l’Amplificatore Ottico di tipo EDFA ma distribuito nel quale cioè
l’amplificazione avviene in Km di fibra ottica. Questo tipo di AO è stato
studiato per molti anni, ma poi si è visto che non era conveniente rispetto
quello a parametri concentrati nel quale grazie ad intense concentrazioni
di Er 3+ si aveva una amplificazione in pochi metri di fibra ottica.
!
!
Un’equazione molto simile a quella ricavata per l’EDFA si ottiene per
altri due tipi di AO distribuiti: l’amplificatore Raman e l’amplificatore
Parametrico (o Kerr).
Nel 1928 C.V.Raman scoprì durante un esperimento che parte della luce
diffusa da un gas o da un liquido presentava un piccolo ma non
trascurabile cambiamento di colore. Raman trovò che la causa era da
addebitare alla interazione fra i fotoni della luce incidente e le vibrazioni
molecolari del gas o del liquido ( quando queste vibrazioni si presentano
collettivamente ordinate, come nei solidi cristallini, esse vengono
chiamate “fononi”). La stessa proprietà fu scoperta quasi
contemporaneamente da scienziati
russi nei solidi cristallini (
Mandel’shtam e Landsberg, 1928). Una analisi spettroscopica della luce
diffusa mostrava che la luce poteva presentare un aumento o una
diminuzione di frequenza. Nel 1962, dopo la scoperta del laser, una
versione “stimolata” dello stesso fenomeno venne scoperta da E.J.
Woodbury: esso è alla base del funzionamento dell’amplificatore Raman
proposto nel 1992 per applicazioni alle comunicazioni ottiche.
Dal punto di vista concettuale, l’amplificatore Raman è il paradigma di
una grande famiglia di amplificatori ottici in cui livelli virtuali
temporanei vengono coinvolti nel meccanismo di amplificazione. Altri
amplificatori ottici che funzionano con lo stesso paradigma sono i già
citati amplificatori Parametrici ed anche gli amplificatori Brillouin .
Tutti gli stati della materia presentano effetto Raman con più o meno
efficienza. Dal punto di vista fisico le vibrazioni molecolari dividono i
livelli elettronici in sotto-livelli secondo strutture molto complesse che
dipendono dal tipo di molecola e dalla sua simmetria. L’effetto Raman si
manifesta come una transizione fra un livello vibrazionale e quello non
Comunicazioni Ottiche, Edizione gennaio 2010, Capitolo 11
immediatamente adiacente: questa transizione avviene mediante un
processo di assorbimento seguito immediatamente da un processo di
emissione (vedi figura).
Quindi l’effetto Raman si manifesta come una combinazione di legge di
assorbimento e di emissione che, come sempre, può essere spontanea e
stimolata ( dando così origine, come nell’amplificatore di tipo EDFA, a
luce rumore spontaneo di tipo ASE o a luce amplificata). Siccome il
processo è regolato da una doppia probabilità, la sezione d’urto
dell’effetto Raman è significativamente più piccola di quella dei normali
processi di assorbimento ed emissione. In principio l’effetto Raman può
avvenire spontaneamente in ambo i sensi, cioè il fotone diffuso può avere
più o meno energia del fotone entrante. Come effetto “stimolato “ si può
invece dimostrare che avviene solo nel senso di produrre un fotone con
energia minore del fotone entrante.
Nello schema seguente sono indicati rispettivamente l’effetto Rayleigh in
cui i fotoni entranti ed uscenti hanno la stessa energia (si parla in questo
caso anche di urto “elastico”) , l’effetto Raman che produce fotoni a
minor energia chiamati anche fotoni Stokes, e l’effetto Raman che
produce fotoni a maggiore energia chiamati anche fotoni Anti-Stokes (si
parla in questi ultimi due casi anche di urto anelastico).
Comunicazioni Ottiche, Edizione gennaio 2010, Capitolo 11
(si noti nella figura la presenza di un livello virtuale indicato come
“tratteggiato”).
Spesse volte l’interazione di diffusione Raman e Rayleigh ha una
rappresentazione semplice in termini di singoli fotoni e di singoli
“fononi” (che sono considerati come particelle) ed è come segue
h" S = h" I # h" P
h" R = h" I
h" AS = h" I + h" P
!
Raman # Stokes process
Rayleight process
Raman # Anti # Stokes process
dove ωP rappresenta la pulsazione del fonone e ωI la pulsazione ella luce
incidente. Tipici valori di ωP sono dell’ordine di centinaia di cm-1 ( il cm-1
è una unità di misura spettroscopica che equivale a 30 GHz) . In
particolare il vetro presenta un picco di presenza di fononi alla frequenza
di 467 cm-1 cui corrisponde una frequenza di circa 13,2 THz. La
diffusione Raman produce quindi un significativo cambiamento di colore
che può arrivare anche ad essere diversi “percento” della frequenza di
ingresso. Siccome 100 cm-1 corrispondono ad energie dell’ordine di 12,4
meV, appare evidente che i “fononi” sono permanentemente eccitati nei
solidi alle normali temperature producendo in questo modo un continuo
di diffusione di luce Raman che si presenta, in uno spettro di frequenza,
come una doppia banda laterale accanto al picco stimolante (vedi figura
in cui sono mostrati anche i picchi Brillouin e Rayleigh).
Comunicazioni Ottiche, Edizione gennaio 2010, Capitolo 11
Nel vetro della fibra ottica questo continuo di frequenze fononiche si
presenta con un andamento molto caratteristico rappresentato in figura.
Si tratta di uno spettro (stimolato) sperimentale ricavato da Doughertj
D.J. nel 1995 per una fibra ottica con un core drogato al 2% di Germanio.
Il picco a 467 cm-1 è ben visibile e si presenta con una larghezza “ a metà
altezza” dell’ordine di 200 cm-1 ( cui corrispondono circa 6 THz che
rappresenta quindi la larghezza di banda “naturale” dell’amplificatore
Raman).
Comunicazioni Ottiche, Edizione gennaio 2010, Capitolo 11
L’effetto Raman è un effetto presente in molti materiali sia gassosi che
liquidi o solidi ed è misurabile in termine di sezione d’urto differenziale
/unità di angolo solido. Spesse volte, per l’effetto Raman stimolato si
preferisce usare una unità di misura più pratica, il coefficiente di
guadagno rapportato alla intensità incidente o g/I in unità di misura di
cm/MW. L’entità di queste grandezze è riportata per confronto nella
tabella seguente per diversi materiali compreso la fibra ottica.
La piccola entità dell’effetto Raman per la fibra ottica è compensata dalla
grande lunghezza di propagazione del segnale ottico. Per tanto, con
lunghezze di diverse decine di Km si ottiene una amplificazione Raman
dello stesso ordine di grandezza della amplificazione EDFA con una
differenza fondamentale: che in questo caso l’amplificazione è un
processo intrinsecamente distribuito. Lo schema tipico di un
amplificatore Raman si presenta quindi come nelle figure seguenti in
configurazione co- e contro-propagante.
Il principio di funzionamento dell’amplificatore Raman è quindi il
seguente. Un fascio piuttosto intenso di “eccitazione “ o di “pompa” entra
in fibra ottica ( esso può essere indifferentemente sia co- che contropropagante). Questo fascio eccita i livelli elettronici delle molecole del
vetro del core della fibra ottica ad uno stato virtuale “alto”. Questa
eccitazione rimane per un tempo sufficientemente lungo per permettere
ad un fotone di segnale di interagire con la stessa molecola e produrre
quindi l’emissione di un fotone “stimolato” alla stessa energia del segnale
+ l’eccitazione di un appropriato fonone ( che pareggia il bilancio
energetico). In altri termini l’inversione di popolazione avviene in questo
caso solo virtualmente e solo temporaneamente: è la presenza
contemporanea del fascio di pompa e di segnale che rende possibile
l’amplificazione che, comunque, avviene sempre per un processo
“stimolato”, come nell’EDFA.
Comunicazioni Ottiche, Edizione gennaio 2010, Capitolo 11
Comunicazioni Ottiche, Edizione gennaio 2010, Capitolo 11
Comunicazioni Ottiche, Edizione gennaio 2010, Capitolo 11
Osservando la figura si può anche immaginare che il processo d’urto crei
un livello virtuale all’interno del materiale (virtuale, perchè non è un
livello stazionario elettronico, ma è un livello “eccitato” ottenuto
mediante il processo d’urto) da cui viene “stimolata” l’emissione Stokes:
in questo senso osservo un’analogia fra lo schema Raman e lo schema di
pompaggio a 3 livelli: è come se l’assorbimento Raman mi producesse un
ripopolamento del livello “virtuale” il quale poi “decade” al livello
fondamentale sotto lo stimolo di un campo ottico di segnale sempre
presente, in modo da produrre amplificazione ottica nella transizione fra
il livello virtuale ed il livello fondamentale.
L’amplificatore Raman prevede quindi che vi sia sempre una pompa
spostata in frequenza di un entità pari alla frequenza del fonone eccitato.
Ad esempio, se questo è alla frequenza più probabile (cioè alla frequenza
con più grande sezione d’urto) cioè 12,5 THz, questi equivalgono attorno
Comunicazioni Ottiche, Edizione gennaio 2010, Capitolo 11
ad 1,5 micron a circa 100 nm. Se quindi voglio amplificare un segnale a
1550 nm (posto in posizione Anti-Stokes), debbo usare una pompa a circa
1450 nm.
In linea di principio, siccome l’effetto Raman avviene in tutto lo spettro
dal visibile al lontano infrarosso, l’amplificatore Raman può operare a
qualsiasi frequenza. Questa caratteristica è di fondamentale importanza
nella ipotesi di estendere la banda occupata dai segnali telecom in tutto il
continuo fra seconda e terza finestra.
Il fenomeno Raman è un fenomeno non-lineare che coinvolge nella sua
formulazione sempre la presenza di due fotoni. Da questo schema di
livelli “virtuale” si evince come mai i fotoni “di pompa” vengano
convertiti in fotoni di segnale direttamente dopo avere “urtato” contro le
molecole di silice. A livello di flusso fotonico si ha che:
" EX = " S
e quindi
!
h" S
h" EX
# EX = h" S # S
h" EX
da cui
!
"S
IEX = IS
" EX
e quindi lo “svuotamento” dell’intensità IEX avviene oltre che per normale
! “attenuazione”, per conversione di IEX in Is con “efficienza” " S /" EX .
Il valore modesto (" 10#13 m /W ) del gRaman è equivalente a quello di un AO
di tipo EDFA molto debolmente! drogato (frazioni di ppb) ed è il motivo
!di tipo Raman è! usato sino ad ora
!
per cui l’Amplificatore Ottico
prevalentemente
in schemi !distribuiti.
!
Per studiare l’amplificazione Raman supponiamo quindi che la variazione
di intensità emessa per via stimolata sia proporzionale attraverso la
sezione d’urto Raman stimolata alla intensità stessa attraverso la classica
relazione di bilancio
dIST = " RSE IST NV dz
dove " RSE è la sezione d’urto microscopica di emissione stimolata Raman,
NV il numero di centri di diffusione Raman e dz il tratto di fibra percorso
!
!
Comunicazioni Ottiche, Edizione gennaio 2010, Capitolo 11
dal segnale. Il parametro " RSE è esprimibile in funzione dell’equivalente
parametro “ spontaneo” dalla relazione
" RSE = " RS
!
IEX
SAT
IEX
!
dove IEX rappresenta l’intensità del fascio di eccitazione o di pompa.
Moltiplicando per h" EX entrambi i termini otteniamo
" RSE = " RS
h# EX IEX
1
IEX
=
SAT
h!# EX IEX
number of propagating exciting modes h# EX
infatti dalla relazione generale
!
Wsat " c = Isat
abbiamo che
!
!
Wsat
I SAT
c = number of propagating exciting modes = EX
h" EX
h" EX
esplicitando cWsat /h" in un materiale con indice di rifrazione n
otteniamo quindi
# 2c 2 I
" RSE = "!RS 2 2 EX
$ ST n h$ EX
!
la misura della sezione d’urto microscopica spontanea si ottiene da una
misura della sezione d’urto differenziale relativa ad un certo angolo
solido ( vedi figura)
Comunicazioni Ottiche, Edizione gennaio 2010, Capitolo 11
per cui abbiamo
$ d " RS '
" RS = &
)d#
% d# (
cioè
!
" RSE =
# 2c 2 IEX & d" RS )
(
+d%
2
$ ST
n 2 h$ EX ' d% *
ed introducendo questa espressione nell’equazione di bilancio
!
dIST =
" 2c 2 IEX
2
# ST
n 2 h# EX
& d$ RS )
(
+d%NV IST dz
' d% *
Definiamo a questo punto un coefficiente di guadagno Raman come
!
gR =
!
' d% RS *
4 " 3c 2
NV
)
,
2
2
# ST n h# EX $# EX ( d& +
(dove è stato supposto una diffusione completamente isotropa integrata
per tutto l’angolo solido # d" = 4$ ) (in letteratura si trova anche una
definizione del coefficiente gR che integra anche il termine IEX) . Valori
tipici di gR/IEX sono riportati nella tabella precedente e per la fibra ottica
-3
sono dell’ordine di
! 0.8 10 cm/MW nel visibile ed inferiori di un paio di
ordini di grandezza (0,810-5 cm/MW) nell’infrarosso. Usando il
coefficiente gR, l’equazione di bilancio diventa
Comunicazioni Ottiche, Edizione gennaio 2010, Capitolo 11
dIST = gR IST IEX dz
!
da cui otteniamo la classica relazione di amplificazione esponenziale
IST = I0ST e g R I EX z
Si noti che il Guadagno G
!
G = eg R z = e
!
- 4 " 3c 2
0
' d% RS *
NV
/ 2 2
)
,I EX 2z
/. # ST n h# EX $# EX ( d& +
21
è funzione esponenziale della Intensità di pompa IEX, del numero di centri
di diffusione NV, della sezione d’urto del processo Raman σRS e della
distanza z percorsa dal segnale in fibra. IOST rappresenta l’intensità di
partenza del segnale. Via via che il segnale propaga in fibra il fascio di
pompa è completamente convertito nel fascio segnale con un andamento
come in figura
Comunicazioni Ottiche, Edizione gennaio 2010, Capitolo 11
A questo risultato occorre aggiungere l’inevitabile effetto di attenuazione
di fibra ottica che agisce contemporaneamente sia sul segnale che sulla
pompa dando luogo al sistema di equazioni tipico dell’amplificazione
distribuita
& dIS
(( dz = "# aS IS + gR IEX IS
'
( dIEX = " $ % g I Is " # I
R EX
EX EX
() dz
$s
dove l’equazione di pompa deriva dalla relazione
!
"s
I p = Is ed i
"p
coefficienti ΣaS e ΣEX sono i coefficienti attenuativi della fibra ottica per
le lunghezze d’onda di segnale e di pompa. L’integrazione del sistema di
equazioni precedente
porta
ad
ottenere! tipici andamenti
dell’amplificazione Raman illustrati nella figura seguente sia per il caso
co- che contro-propagante.
Comunicazioni Ottiche, Edizione gennaio 2010, Capitolo 11
Comunicazioni Ottiche, Edizione gennaio 2010, Capitolo 11