ESERCIZIO: DARLINGTON #1
IC1
B
C
IC
IB
vπ1 rπ1
ro1
-
IC2
B
C
gm1vπ1
+
+
gm2vπ2
vπ2 rπ2
IE1
IE
ro2
-
E
E
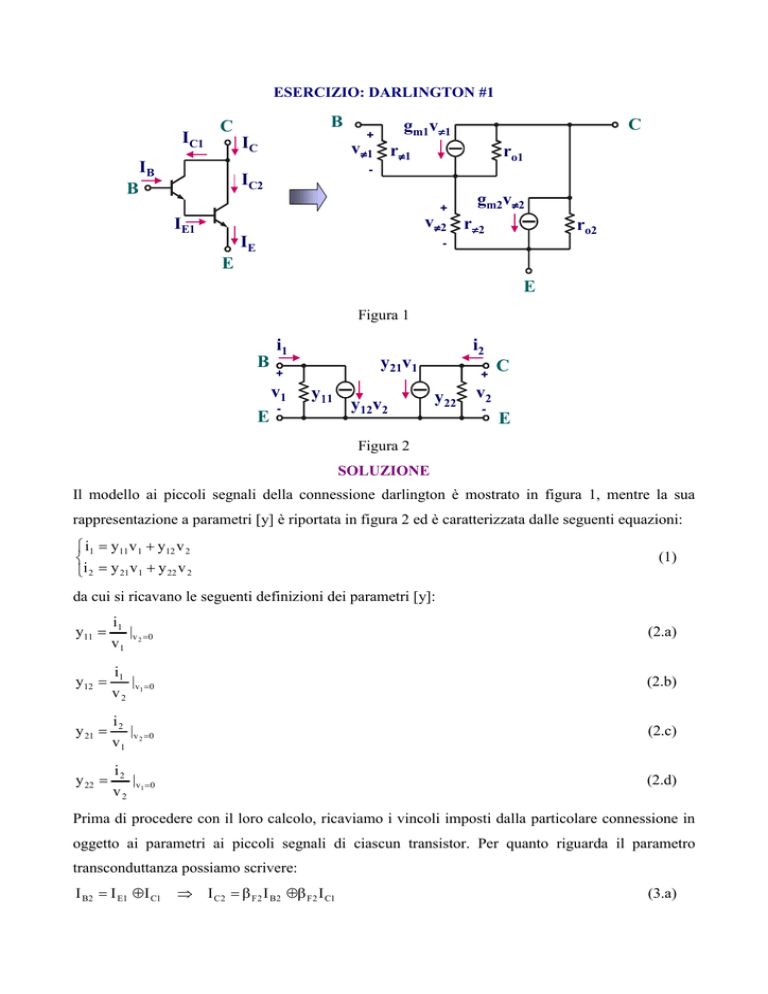
Figura 1
B
i1
+
v1
E
-
i2
y21v1
y11
y12v2
+
y22
C
v2
-
E
Figura 2
SOLUZIONE
Il modello ai piccoli segnali della connessione darlington è mostrato in figura 1, mentre la sua
rappresentazione a parametri [y] è riportata in figura 2 ed è caratterizzata dalle seguenti equazioni:
i1 = y11 v 1 + y12 v 2
i 2 = y 21 v 1 + y 22 v 2
(1)
da cui si ricavano le seguenti definizioni dei parametri [y]:
y11 =
i1
|v =0
v1 2
(2.a)
y12 =
i1
|v = 0
v2 1
(2.b)
y 21 =
i2
|v =0
v1 2
(2.c)
y 22 =
i2
|v = 0
v2 1
(2.d)
Prima di procedere con il loro calcolo, ricaviamo i vincoli imposti dalla particolare connessione in
oggetto ai parametri ai piccoli segnali di ciascun transistor. Per quanto riguarda il parametro
transconduttanza possiamo scrivere:
I B2 = I E1 ≈ I C1
⇒ I C 2 = β F 2 I B2 ≈ β F 2 I C1
(3.a)
da cui,
g m2 =
I C 2 β F 2 I C1
≈
= β F 2 g m1
VT
VT
⇒ g m 2 ≈ β 02 g m1
(3.b)
Di conseguenza, le resistenze di ingresso devono soddisfare la seguente relazione:
rπ 2 =
β 02
r
1
≈
= π1
g m 2 g m1 β 01
(4)
Per quanto riguarda le resistenze di uscita possiamo scrivere:
ro1 =
VCE1 + VA VA VA I C 2
≈
=
≈ β 02 ro 2
I C1
I C1 I C 2 I C1
(5)
Per il calcolo dei parametri [y], facciamo riferimento alle figure 3 e 4, nelle quali si è considerato
v1 = 0 e v2 = 0 rispettivamente. Le espressione approssimate ricavate in seguito considerano β0 >>1.
i2
β01i1
+
i1 rπ1
+
ro1
io1
vπ1
-
gm2vπ2
+
vπ2= -vπ1 rπ2
C
v2
ro2
-
-
E
Figura 3
i1
B
+
rπ1
i2
+
gm1vπ1
ro1
io1
vπ1
-
v1
+
E
-
gm2vπ2
vπ2 rπ2
ro2
-
Figura 4
Determinazione di y11:
Il parametro y11 rappresenta la conduttanza di ingresso quando viene annullata la tensione di uscita.
Il circuito da analizzare è pertanto quello mostrato in figura 4 nel quale si è posto l'uscita in
cortocircuito e si è applicato un generatore di tensione v1 in ingresso. Da questo schema si calcola il
rapporto i1/v1 come segue:
v 1 = rπ1i1 + (ro1 // rπ 2 )(1 + β 01 )i1
(6)
1
1
1
1
≈
=
=
rπ1 + (ro1 // rπ 2 )(1 + β 01 ) rπ1 + rπ 2β 01 2rπ1 2 rπ 2β 01
y11 =
(7)
dove si è fatto uso della (4) e si è considerato ro1 // rπ 2 ≈ rπ 2 dato che
rπ 2 ≈
V
V V
V
1
= T = T A ≈ T ro1 << ro1
g m1 I C1 VA I C1 VA
(8)
Determinazione di y12:
Il parametro y12 rappresenta la transconduttanza inversa con la porta di ingresso cortocircuitata. Il
circuito da analizzare è mostrato in figura 3. Da questo schema otteniamo:
i1 = −
i 01 =
rπ 2
(β 01i1 + i 01 )
rπ1 + rπ 2
(9)
v 2 − (rπ 2 // rπ1 )(β 01i1 + i 01 )
⇒ i 01 =
r01
v 2 (rπ 2 // rπ1 )
−
β 01i1
(r // r ) r
r01
1 + π 2 π1 01
r01
1
(10)
Sostituendo la (10) equazione nella (9) otteniamo:
i1 = −
rπ 2
(β 01i1 ) − rπ2
rπ1 + rπ 2
rπ1 + rπ 2
v 2 (rπ 2 // rπ1 )
1
β 01i1
−
r01
r01
1 + (rπ 2 // rπ1 )
r01
(11)
Da questa relazione possiamo trovare l'espressione esatta del parametro y12. Tuttavia, per capire se
possiamo trascurarlo o meno abbiamo bisogno di una espressione più semplice che possiamo
derivare nel seguente modo:
Notiamo, innanzitutto, che il termine
rπ 2
può essere così semplificato (si faccia uso della (4)):
rπ1 + rπ 2
rπ 2
rπ 2
1
=
=
rπ1 + rπ 2 β 01 rπ 2 + rπ 2 β 01 + 1
(12)
e consideriamo, inoltre:
rπ 2 // rπ1 ≈ rπ 2 // (β 01rπ 2 ) ≈ rπ 2
(13)
Usando tali approssimazioni e considerando la (8), la (11) diventa:
v
r
i1 = − i1 − 2 − π 2
β 01 r01 r01
da cui si ricava:
1
i1
1 + rπ 2
r01
⇒ 2i1 ≈ −
v2
β 01r01
(14)
y12 ≈ −
1
2β 01r01
≈0
(15)
Determinazione di y21:
Il parametro y21 rappresenta la transconduttanza diretta con l'uscita in cortocircuito. Per la sua
determinazione si faccia uso della figura 4. Da questo schema calcoliamo:
1
i 2 = g m1 v π1 + g m 2 v π 2 + i 01 = g m1 v π1 + v π 2 g m 2 −
r01
(16)
Dalla maglia di ingresso osserviamo che:
(r // r )
v 1 = v π1 + v π 2 = v π1 1 + π 2 01 (1 + β 01 ) ≈ 2 v π1
rπ1
⇒ v π1 ≈ v π 2
(17)
per cui sostituendo nella (16) otteniamo (si ricordi la relazione (3.b)):
i2 ≈
v1
(g m1 + g m 2 ) ⇒
2
y 21 ≈
g m2
2
(18)
Determinazione di y22:
Il parametro y22 rappresenta la conduttanza di uscita quando viene cortocircuitata la porta di
ingresso. Il circuito da analizzare rimane quello di figura 3. Calcoliamo, innanzitutto, la resistenza
di uscita del primo transistor che coincide con la resistenza di uscita di uno stadio emettitore
comune con resistenza di emettitore, cioè:
g m1rπ 2
ro′1 = ro1 1 +
≈ 2 ro1
rπ 2
1+
rπ1
(19)
La corrente di uscita i2 risulta:
i2 =
v
v2
v
v
v
+ g m 2 v π 2 + 2 = 2 + 2 + g m 2 2 (rπ1 // rπ 2 )
ro′1
ro 2 ro′1 ro 2
ro′1
(20)
da cui, facendo uso della (5), si ottiene:
y 22 ≈
1
1
(1 + β 02 ) ≈ 1 + 1 = 3
+
ro 2 2ro1
ro 2 2 ro 2 2 ro 2
(21)
In definitiva, la connessione darlington può essere trattata alla stregua di un singolo transistor
avente il seguente modello ai piccoli segnali:
B
+
rπ
C
gmvπ
ro
vπ
-
E
Figura 5
in cui i parametri valgono:
rπ ≈ 2β 01 rπ 2
(22.a)
g m2
2
(22.b)
2
ro ≈ ro 2
3
(22.c)
gm ≈