Doppi bipoli

Doppi bipoli
www.die.ing.unibo.it/pers/mastri/didattica.htm
(versione del 21-11-2012)
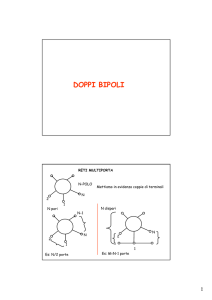
Doppi bipoli (o 2-porte)
● Doppi bipoli: componenti con due copie di terminali (porte) tali
che, per ciascuna coppia, la corrente entrante in uno dei terminali
è uguale a quella uscente dall’altro
● Doppio bipolo intrinseco:
 il vincolo tra le correnti dei terminali di ciascuna porta è
determinato dalla struttura interna del componente
● Doppio bipolo non intrinseco:
 il vincolo tra le correnti è dovuto al modo in cui il componente
viene collegato
i2  i1
i4  i3
2
Rappresentazioni di un tripolo come doppio bipolo
● Un tripolo può essere considerato come un doppio bipolo con i
terminali negativi delle porte collegati tra loro
● Le tensioni e le correnti utilizzate per caratterizzare il componente e le espressioni delle equazioni caratteristiche dipendono
dalla scelta del terminale comune
3
Doppi bipoli resistivi
● Le equazioni di un doppio bipolo resistivo sono del tipo
f1 v1 (t ), v2 (t ), i1 (t ), i2 (t ), t   0
f 2 v1 (t ), v2 (t ), i1 (t ), i2 (t ), t   0
f1, f2  funzioni generiche
● Se il tempo non compare esplicitamente come argomento di f1 e
f2 il componente è detto tempo-invariante
4
Doppi bipoli resistivi lineari tempo-invarianti
● Per un doppio bipolo resistivo lineare e tempo-invariante
le equazioni, nel caso generale, sono del tipo
a11v1  a12 v2  b11i1  b12i2  0
a21v1  a22 v2  b21i1  b22i2  0
aij, bij (i, j  1, 2) rappresentano delle costanti reali
● Queste equazioni possono essere espresse nella forma
Av  Bi  0
dove
v 
v   1
v2 
i 
i   1
i2 
a
A   11
a21
a12 
a22 
b 
b
B   11 12 
b21 b22 
● Quando è possibile esplicitare due delle variabili in funzioni delle
rimanenti si possono avere altre forme particolari delle equazioni
5
Rappresentazioni di un doppio bipolo
Rappresentazione
Variabili
Variabili
indipendenti dipendenti
Comandata in corrente
i1, i2
v1, v2
Comandata in tensione
v1, v2
i1, i2
Ibrida (diretta)
i1, v2
v1, i2
Ibrida inversa
v1, i2
i1, v2
Trasmissione (diretta)
v2, i2
v1, i1
Trasmissione inversa
v1, i1
v2, i2
6
Matrice di resistenza
● Per un doppio bipolo comandato in corrente le equazioni
possono essere poste nella forma
v1  r11i1  r12i2
v2  r21i1  r22i2
cioè
v  Ri
dove
 v1 
v 
v2 
 i1 
i 
i2 
 r11
R
r21
r12 
r22 
● R = matrice di resistenza
● Per comprendere il significato dei parametri, si considerano le
condizioni di funzionamento in cui una delle variabili indipendenti
viene azzerata (mentre l’altra assume un valore arbitrario  0)
7
Significato dei parametri di resistenza
r11 
v1
i1 i 0
r21 
2
v2
i1
i2  0
 r11  resistenza di ingresso a vuoto alla porta 1
 r21  resistenza di trasferimento a vuoto dalla porta 1 alla porta 2
r22 
v2
i2
r12 
i1  0
v1
i2
i1  0
 r22  resistenza di ingresso a vuoto alla porta 2
 r12  resistenza di trasferimento a vuoto dalla porta 2 alla porta 1
8
Esempio – Resistori collegati a T
 R  RC
R A
 RC
v1  RA  RC i1
v2  RCi1
RC 
RB  RC 
v1  RCi2
v2  RB  RC i2
9
Esempio – Resistori collegati a Π
 RAB RAC  RAC RBC
 R R R
AC
BC
R   AB
R
R
AC BC

 RAB  RAC  RBC
RAC RAB  RBC 
RAC  RAB  RBC
RAC
v2  i1
RBC
RAC  RAB  RBC
v1  i1
RAC RBC

RAB  RAC  RBC 

RAB RBC  RAC RBC 
RAB  RAC  RBC 
RBC RAB  RAC 
RBC  RAC  RAB
RBC
RAC
v1  i2
RAC  RAB  RBC
v2  i2
10
Esempio – Equivalenza T – Π (stella-triangolo)
● Un doppio bipolo a T e un doppio bipolo a Π sono equivalenti se
le loro matrici di resistenza RT e R sono uguali
 R  RC
RT   A
 RC
RC 
RB  RC 
 RAB RAC  RAC RBC
 R R R
AC
BC
R    AB
RAC RBC

 RAB  RAC  RBC
RAC RBC

RAB  RAC  RBC 

RAB RBC  RAC RBC 
RAB  RAC  RBC 
● Confrontando le matrici si riconosce che devono essere verificate
le relazioni
RAB RAC
RAB RBC
RAC RBC
RA 
RB 
RC 
RAB  RAC  RBC
RAB  RAC  RBC
RAB  RAC  RBC
che corrispondono alle formule di trasformazione triangolo-stella
11
Matrice di conduttanza
● Per un doppio bipolo comandato in tensione le equazioni
possono essere poste nella forma
i1  g11v1  g12 v2
i2  g 21v1  g 22 v2
cioè
i  Gv
dove
 v1 
v 
v2 
 i1 
i 
i2 
 g11
G
 g 21
g12 
g 22 
● G = matrice di conduttanza
12
Significato dei parametri di conduttanza
g11 
i1
v1 v 0
g 21 
2
i2
v1
v2  0
 g11  conduttanza di ingresso in cortocircuito alla porta 1
 g21  conduttanza di trasferimento in cortocircuito dalla porta 1 alla porta 2
g 22 
i2
v2
g12 
v1  0
i1
v2
v1  0
 g22  conduttanza di ingresso in cortocircuito alla porta 2
 g12  conduttanza di trasferimento in cortocircuito dalla porta 2 alla porta 1
13
Esempio – Resistori collegati a Π
G  GAC
G   AB
  GAB
i1  v1 GAB  GAC 
i2  v1GAB
 GAB 
GAB  GBC 
i1  v2GAB
i2  v2 GAB  GBC 
14
Esempio – Resistori collegati a T
 GA GB  GA GC
 G G G
B
C
G A
G
G
A B

 GA  GB  GC
GA GB  GC 
GA  GB  GC
G G  GC 
GB
i2  v1 A B

GA  GB  GC GB  GC
i1  v1
GA GB

GA  GB  GC 

GA GB  GBGC 
GA  GB  GC 

GB GA  GC 
GB  GA  GC
G G  GC 
GA
i1  v2 B A

GB  GA  GC GA  GC
i2  v2
15
Matrici ibride
● Se è possibile esprimere v1 e i2 in funzione di i1 e v2 si ha
v1  h11i1  h12 v2
i2  h21i1  h22 v2
 i1 
v1 
 i   H  v 
 2
 2
h
H   11
h21
h12 
h22 
● H  matrice ibrida (diretta)
● Se è possibile esprimere i1 e v2 in funzione di v1 e i2 si ha
i1  h11 v1  h12 i2
 v1  h22
 i2
v2  h21
 i1 
v1 



H
v 
i 
 2
 2
 h11
H  

h21
h12 
 
h22
● H  matrice ibrida inversa
● I coefficienti delle matrici ibride non hanno dimensioni omogenee
16
Significato dei coefficienti di H
h11 
v1
i1
h21 
v2  0
i2
i1
v2  0
 h11  resistenza di ingresso in cortocircuito alla porta 1
 h21  guadagno di corrente in cortocircuito dalla porta 1 alla porta 2
h12 
v1
v2
h22 
i1  0
i2
v2
i1  0
 h22  conduttanza di ingresso a vuoto alla porta 2
 h12  guadagno di tensione a vuoto dalla porta 2 alla porta 1
17
Significato dei coefficienti di H
h11 
i1
v1
 
h21
i2  0
v2
v1
i2  0
 h11  conduttanza di ingresso a vuoto alla porta 1
  guadagno di tensione a vuoto dalla porta 1 alla porta 2
 h21
h12 
i1
i2
 
h22
v1  0
v2
i2
v1  0
  resistenza di ingresso in cortocircuito alla porta 2
 h22
 h12  guadagno di corrente in cortocircuito dalla porta 2 alla porta 1
18
Matrice di trasmissione (matrice catena)
● Si esprimono la tensione e la corrente alla porta 1 in funzione della
tensione e della corrente alla porta 2
● Per motivi pratici, conviene considerare come variabile indipendente i2
invece di i2
v1  Av2  Bi2
A B
T

C D 
v1 
 v2 
T


i 
 i 
 1
 2
i1  Cv2  Di2
● T  matrice di trasmissione (matrice catena)
● Significato dei coefficienti
A
v1
v2
B
i2  0
v1
 i2
C
v2  0
i1
v2
D
i2  0
i1
 i2
v2  0
● Non è possibile utilizzare queste relazioni per determinare i coefficienti
(occorrerebbe fissare sia la tensione che la corrente della porta 2)
19
Determinazione dei coefficienti di T
1 v2

A v1
1 v2

C i1
i2  0
1  i2

B v1
v2  0
i2  0
1  i2

D
i1
v2  0
20
Matrice di trasmissione inversa
● Si esprimono la tensione e la corrente alla porta 2 in funzione della
tensione e della corrente alla porta 1
● Per motivi pratici, conviene considerare come variabile indipendente i1
invece di i1
v2  Av1  Bi1
i2  C v1  Di1
 A B 
T  

C  D
v2 
 v1 

T


i 
 i 
 2
 1
● T  matrice di trasmissione inversa
● Significato dei coefficienti
A 
v2
v1
B 
i1  0
v2
 i1
C 
v1  0
i2
v1
D 
i1  0
i2
 i1
v1  0
21
Relazioni tra le rappresentazioni
● Confrontando le varie espressioni delle equazioni di un doppio
bipolo si riconosce che (quando il doppio bipolo ammette tutte le
rappresentazioni considerate)
 la matrice G è l’inversa della matrice R
 la matrice H è l’inversa della matrice H
 La matrice T è l’inversa della matrice T con i coefficienti della
diagonale secondaria cambiati di segno a causa delle scelte
diverse per i versi di riferimento delle correnti
● Le altre relazioni tra le varie rappresentazioni si possono ottenere
utilizzando le definizioni dei coefficienti delle matrici
22
Esempio - Passaggio da parametri r a parametri h
v1  r11i1  r12i2

v2  r21i1  r22i2
v1  h11i1  h12 v2
i2  h21i1  h22 v2
● Calcolo degli elementi della prima colonna di H
v1
i1
h11 
h21 
v2  0
v2  0

(si pone v2  0)
v2  0
v1  r11i1  r12i2

h11 
i2
i1
0  r21i1  r22i2
det(R )
r22
h21  
i2  

r21
i1
r22

r 
det(R )
v1   r11  r12 21  i1 
i1
r22 
r22

r21
r22
23
Esempio - Passaggio da parametri r a parametri h
v1  r11i1  r12i2
v2  r21i1  r22i2

v1  h11i1  h12 v2
i2  h21i1  h22 v2
● Calcolo degli elementi della seconda colonna di H
h12 
v1
v2
h22 
i1  0
i1  0


h12 
r12
r22
i2
v2
(si pone i1  0)
i1  0
v1  r12i2
v2  r22i2
h22 

i2 
1
v2
r22
v1 
r12
v2
r22
1
r22
24
Relazioni tra le rappresentazioni
R
R
G
r11
r12
r21
r22
r22
R

G
r21

R
R
r22
H
r
 21
r22
1
r11
H
r21
r11
r11
r21
T
1
r21
r22
r21
T
1
r12
r12
R
r11
R
r12
r22
1
r22
r
 12
r11
R
r11
R
r21
r22
r21
R
r12
r11
r12

g 22
G
g
 21
G
g11
g 21
1
g11
g 21
g11
G
g 22
g
 21
g 22
g
 22
g 21
G

g 21
g
 11
g12
G

g12
g
 12
G
g11
G
g12
g 22
g12
g11
G
g11
g12
g 22
1
g 22
1

g 21
g
 11
g 21
1

g12
g
 11
g12

H
H h12
h22
h22
1
h21

h22 h22
1
h
 12
h11
h11
h21 H
h11
h11
h11
h12
h21
h22
h22
h
 12
H
H
h
h11
 21
H H
h
H

 11
h21
h21
1
h
 22 
h21
h21
h11
1
h12 h12
h22 H
h12 h12
H
1
h
 12
h11
h11

h21
H
h11
h11
H h12


h22
h22

h21
1



h22
h22

h22
h
 12
H
H
h
h11
 21
H
H
h11

h21
1

h21
h11

h21
H 

h12
h
 11
h12
h12

h22

h22

h21
H 

h21
h
 22
h12
1

h12
T
A T
C C
1
D
C C
D
T

B
B
A
1

B
B
B
T
D
D
C
1

D D
T
C

A
A
1
B
A
A
A
B
C
D
D
T
C
T
B
T
A
T
T
1
D
C C
T A
C C
A
1

B
B
T D

B
B

B
1
A
A
T C 

A A
1
C


D
D
A
T
D
D
D
B
T T
C
A
T T
A B
C  D
Μ  det(M )
Ogni riga riporta le espressioni dei coefficienti di una matrice in funzione
dei coefficienti delle matrici indicate nelle intestazioni delle colonne
25
Esempio – doppi bipoli che non ammettono la
matrice R o la matrice G
v1  v2  R (i1  i2 )
 v1   R
v    R
 2 
R   i1 

R  i2 
R R
R

R R
● Non è possibile imporre valori arbitrari ad entrambe le tensioni (cioè
utilizzarle come variabili indipendenti)  la matrice G non è definita
i1  i2  G (v1  v2 )
 i1   G  G   v1 
i    G G   v 
  2
 2 
 G  G
G

 G G 
● Non è possibile utilizzare le correnti come variabili indipendenti
 la matrice R non è definita
26
Reciprocità
● Ipotesi:
v1, v2 , i1, i2 
v1, v2, i1, i2 
insiemi arbitrari di tensioni e correnti che
soddisfano le equazioni del doppio bipolo
● Definizione:
si dice che il doppio bipolo è reciproco se
v1i1  v2 i2  v1i1  v2i2
● Per interpretare il significato di questa relazione e ricavare le
condizioni che devono soddisfare i parametri delle matrici del
doppio bipolo si fa riferimento alle situazioni in cui una sola delle
variabili indipendenti è diversa da zero
27
Reciprocità - parametri r
Condizione 1
i1  I
Condizione 2
i2  0
i1  0
v2  r21i1  r22i2  r21 I
i2  I
v1  r11i1  r12i2  r12 I
Condizione di reciprocità
v1i1  v2 i2  v1i1  v2i2


v1  0  v2 I  v1I  v2  0

v2  v1
r12  r21
28
Reciprocità - parametri g
Condizione 1
v1  V
Condizione 2
v2  0
v1  0
i2  g 21v1  g 22 v2  g 21 V
v2  V
i1  g11v1  g12 v2  g12 V
Condizione di reciprocità
v1i1  v2 i2  v1i1  v2i2


V i1  0  i2  0  i1  V i2

i2  i1
g12  g 21
29
Reciprocità - parametri h
Condizione 1
i1  I
Condizione 2
v2  0
i1  0
i2  h21i1  h22 v2  h21 I
v2  V
v1  h11i1  h12 v2  h12 V
Condizione di reciprocità
v1i1  v2 i2  v1i1  v2i2

v1  0  0  i2  v1 I  V i2

h12  h21

i2
v
 1
I
V
30
Reciprocità - parametri h, T e T
● Parametri h:
 procedendo in modo simile al caso precedente si ottiene la
condizione

h12  h21
● Parametri di trasmissione:
 si può dimostrare che per un doppio bipolo reciproco valgono
le condizioni
det(T)  1
det(T)  1
31
Doppi bipoli reciproci
● Per un doppio bipolo reciproco valgono le seguenti proprietà:
 Applicando una corrente I ad una qualunque delle porte
all’altra porta si ottiene la stessa tensione a vuoto
 Applicando una tensione V ad una qualunque delle porte
all’altra porta si ottiene la stessa corrente di cortocircuito
 Il guadagno di corrente in cortocircuito in una direzione è
uguale al guadagno di tensione a vuoto nella direzione
opposta cambiato di segno
32
Simmetria
● Si dice che un doppio bipolo è simmetrico se, per ogni insieme
di tensioni e di correnti alle porte che soddisfano le sue equazioni
caratteristiche, anche l’insieme ottenuto scambiando la porta 1
con la porta 2 soddisfa le equazioni caratteristiche
● Si può dimostrare che le matrici di un due porte simmetrico
soddisfano le seguenti proprietà
 matrice R:
r11  r22
r12  r21
 matrice G:
g11  g22
g12  g21
 matrice H:
h12  h21 det(H)  1
 matrice H: h12  h21 det (H)  1
 matrice T:
AD
det(T)  1
 matrice T: A’  D’
det(T)  1
 La simmetria implica anche la reciprocità
33
Trasformatore ideale
● Le equazioni del trasformatore ideale possono essere espresse
intermini di matrice ibrida o di matrice di trasmissione (dirette o inverse)
Parametri di
trasmissione
v1  Kv2
i1  
1
i2
K
Parametri
ibridi
v1  Kv2
i2   Ki1
K  rapporto di trasformazione o rapporto spire
● Per il trasformatore ideale non è possibile definire le matrici R e G
● Vale la relazione h12  h21  K
 Il trasformatore ideale è un componente reciproco
(ma non simmetrico, se K ≠ 1 )
34
Generatori dipendenti
Generatore di tensione
controllato in corrente
v1  0
v2  ri1

 v1  0 0  i1 
v    r 0  i 
  2
 2 
Caso particolare di rappresentazione
in termini di parametri di resistenza
r11  r12  r22  0
Generatore di corrente
controllato in tensione
i1  0
i2  gv1

r21  r
 i1   0 0  v1 
i    g 0  v 
  2
 2 
Caso particolare di rappresentazione
in termini di parametri di conduttanza
g11  g12  g 22  0
g 21  g
35
Generatori dipendenti
Generatore di corrente
controllato in corrente
v1  0
i2  i1

v1   0 0  i1 
 i     0   v 
  2
 2 
Caso particolare di rappresentazione
in termini di parametri ibridi (diretti)
h11  h12  h22  0
Generatore di tensione
controllato in tensione
i1  0
v2  v1

h21  
 i1   0 0 v1 
v    0   i 
  2
 2 
Caso particolare di rappresentazione
in termini di parametri ibridi (inversi)
 0
h11  h12  h22
 
h21
36
Generatori dipendenti
● I quattro tipi di generatori dipendenti corrispondono a matrici R, G, H e
H’ con il solo elemento 21 diverso da zero
 I generatori dipendenti sono componenti non reciproci
● Ciascun tipo di generatore ammette una sola tra le matrici R, G, H e H’
● Si può verificare che l’unica altra matrice definita in tutti e quattro i casi
è la matrice T
● I doppi bipoli (e più in generale i componenti N-porte) lineari resistivi
possono essere rappresentati mediante circuiti equivalenti formati da
generatori dipendenti e resistori
 In questo modo è possibile estendere i metodi di analisi studiati in
Elettrotecnica ai circuiti che contengono doppi bipoli (e N-porte)
37
Circuiti equivalenti di doppi bipoli lineari
Matrice di resistenza
v1  r11i1  r12i2
v2  r21i1  r22i2
Matrice di conduttanza
i1  g11v1  g12 v2
i2  g 21v1  g 22 v2
38
Circuiti equivalenti di doppi bipoli lineari
Matrice H
v1  h11i1  h12 v2
i2  h21i1  h22 v2
Matrice H
i1  h11 v1  h12 i2
 v1  h22
 i2
v2  h21
39
Circuiti equivalenti di doppi bipoli lineari
Circuiti equivalenti a T
Doppio bipolo reciproco
v1  r11i1  r12i2
v2  r12i1  r22i2
Doppio bipolo non reciproco
v1  r11i1  r12i2
v2  r21i1  r22i2
40
Circuiti equivalenti di doppi bipoli lineari
Circuiti equivalenti a Π
Doppio bipolo reciproco
i1  g11v1  g12 v2
i2  g12 v1  g 22 v2
Doppio bipolo non reciproco
i1  g11v1  g12 v2
i2  g 21v1  g 22 v2
41
Teoremi di rappresentazione dei doppi bipoli
Rappresentazione comandata in corrente
● Ipotesi:
 Q  doppio bipolo formato da componenti resistivi lineari e
generatori indipendenti
 Q è comandato in corrente
 Circuito equivalente:
 vG1, vG2  tensioni a vuoto alle porte di Q
(v1 e v2 per i1  i2  0)
 R  matrice di resistenza del doppio bipolo ottenuto da Q
azzerando i generatori indipendenti
42
Teoremi di rappresentazione dei doppi bipoli
Rappresentazione comandata in tensione
● Ipotesi:
 Q  doppio bipolo formato da componenti resistivi lineari e
generatori indipendenti
 Q è comandato in tensione
 Circuito equivalente:
 iG1, iG2  correnti di cortocircuito alle porte di Q
(i1 e i2 per v1  v2  0)
 G  matrice di conduttanza del doppio bipolo ottenuto da Q
azzerando i generatori indipendenti
43
Teoremi di rappresentazione dei doppi bipoli
Rappresentazione ibrida (diretta)
● Ipotesi:
 Q  doppio bipolo formato da componenti resistivi lineari e
generatori indipendenti
 Q ammette la rappresentazione ibrida (diretta)
 Circuito equivalente:
 vG1  v1 per i1  0, v2  0
 iG2  i2 per i1  0, v2  0
 H  matrice ibrida (diretta) del doppio bipolo ottenuto da Q
azzerando i generatori indipendenti
44
Collegamenti di bipoli e doppi bipoli
● Di seguito si prenderanno in esame alcuni casi in cui un doppio bipolo
è ottenuto collegando due doppi bipoli oppure collegando un doppio
bipolo con uno più bipoli
● In tutti i casi si sottintende che siano soddisfatte le seguenti ipotesi
(che nei casi pratici dovranno sottoposte a verifica)
 I collegamenti considerati sono leciti (cioè non dànno origine a
circuiti impossibili o indeterminati)
 Le matrici utilizzate per rappresentare i doppi bipoli sono definite
 Nel caso di doppi bipoli non intrinseci, i componenti, collegati nei
modi considerati, si comportano effettivamente come doppi bipoli
45
Resistori in serie alle porte
● In questo caso conviene utilizzare i parametri di resistenza

r 
R   11
r21
r12 
r22 
v1  R1i1  v1  R1  r11 i1  r12 i2
v2  R2i2  v2  r21 i1  R2  r22 i2

r   R1
R   11
r21
r12

r22  R2 
 Le resistenze in serie alle porte si sommano alle resistenze di ingresso
46
Resistori in parallelo alle porte
● In questo caso conviene utilizzare i parametri di conduttanza

g
G    11

 g 21
 
g12
 
g 22
 v1  g12
 v2
i1  G1v1  i1  G1  g11
 v1  G2  g 22
 v2
i2  G2 v2  i2  g 21

 g   G1
G   11

 g 21

g12

  G2 
g 22
 Le conduttanze dei resistori in parallelo alle porte si sommano alle
conduttanze di ingresso
47
Doppi bipoli in serie
● LKI:
i1  i1a  i1b
i2  i2 a  i2b
 i  i a  ib
● LKV:
v1  v1a  v1b
v2  v2 a  v2 b
 v  v a  vb
● Componenti:
v a  R ai a
vb  R bib

v  (R a  R b )i  v  Ri

R  Ra  Rb
● La matrice R del doppio bipolo risultante è data dalla somma delle
matrici di resistenza dei due doppi bipoli
48
Resistore in serie al terminale comune di un tripolo
● Questo collegamento può essere visto come un caso particolare di
collegamento in serie di doppi bipoli
r
R a   11
r21
r12 
r22 
R R
Rb  

R R
 r  R r12  R 
R  R a  R b   11

r21  R r22  R 
 R si somma a tutti gli elementi della matrice Ra
49
Doppi bipoli in parallelo
● LKV:
v1  v1a  v1b
v2  v2 a  v2 b
 v  va  vb
● LKI:
i1  i1a  i1b
i2  i2 a  i2b
 i  i a  ib
● Componenti:
ia  Ga va
ib  G b vb

i  (G a  G b ) v  i  Gv

G  Ga  Gb
 La matrice G del doppio bipolo risultante è data dalla somma delle
matrici di conduttanza dei due doppi bipoli
50
Resistore collegato tra le due porte
● Questo può essere visto come un caso particolare di collegamento in
parallelo di doppi bipoli
g
G a   11
 g 21
g12 
 G  G
G

b
 G G 
g 22 


g  G
G  G a  G b   11
 g 21  G
g12  G 
g 22  G 
 G si somma agli elementi della diagonale principale e si sottrae dagli
elementi della diagonale secondaria della matrice Ga
51
Collegamento serie-parallelo
● LKV:
v1  v1a  v1b
v2  v2 a  v2 b
● LKI:
i1  i1a  i1b
i2  i2 a  i2b
● Componenti:
v1a 
 i1a  v1b 
 i1b 
 i   H a v   i   H b  v 
 2a 
 2 a   2b 
 2b 
v1 
 i1 
 i1 


H
H
H




 i 
a
b
v 
v 
 2
 2
 2

H  H a  Hb
 La matrice H del doppio bipolo risultante è data dalla somma delle
matrici ibride dei due doppi bipoli
52
Collegamento parallelo-serie
● LKV:
v1  v1a  v1b
v2  v2 a  v2 b
● LKI:
i1  i1a  i1b
i2  i2 a  i2b
● Componenti:
 i1a 
v1a   i1b 
v1b 


H
H


b
a
v 
  

 2a 
 i2 a  v2b 
 i2b 
 i1 
v1 
v1 





H
H
H




 v 
a
b
i 
i 
2
 
 2
 2

H  Ha  Hb
 La matrice H del doppio bipolo risultante è data dalla somma delle
matrici ibride inverse dei due doppi bipoli
53
Doppi bipoli in cascata
● In questo caso conviene utilizzare le matrici di trasmissione
 v2 a 
v1 
T

a

i 
 1
 i2 a 
v1b 
 v2 
T

b
i 

 i2 
 1b 
● Le tensioni e le correnti alla porta comune coincidono
v1b  v2 a
i1b  i2 a
v1 
 v2 
T
T


  i  a b  i 
 T  Ta  Tb
 1
 2
 La matrice T del doppio bipolo risultante è data dal prodotto delle
matrici di trasmissione dei due doppi bipoli
54
Doppi bipoli terminati
Sorgente
Doppio
bipolo
Carico
● Nelle applicazioni pratiche si incontra spesso il caso in cui le porte di un
doppio bipolo sono collegate a due bipoli come mostrato nella figura
● Il primo bipolo costituisce la sorgente del segnale in ingresso al doppio
bipolo e può rappresentare il circuito equivalente di Thévenin o Norton
degli stati precedenti
● Il secondo bipolo costituisce il carico e può rappresentare l’impedenza
equivalente degli stati successivi
55
Indici degli elementi delle matrici del doppio bipolo
● Quando un doppio bipolo è utilizzato in modo che è possibile attribuire
alle due porte i ruoli di ingresso e di uscita, gli indici degli elementi delle
matrici del doppio bipolo vengono indicati anche nel modo seguente
 11  i (input)
 il parametro esprime la relazione tra la
tensione e la corrente alla porta di ingresso
 21  f (forward)  il parametro indica come ciò che avviene
alla porta di ingresso influenza l’uscita
 12  r (reverse)  il parametro indica come ciò che avviene
alla porta di uscita influenza l’ingresso
 22  o (output)
r
R i
rf
rr 
ro 
 il parametro esprime la relazione tra la
tensione e la corrente alla porta di uscita
g
G i
 gf
gr 
g o 
h
H i
hf
hr 
ho 
56
Doppi bipoli unilaterali
● Un doppio bipolo per cui il parametro r è nullo è detto unilaterale
 Un doppio bipolo unilaterale è un componente non reciproco
● In queste condizioni si può avere propagazione del segnale solo dalla
porta 1 alla porta 2
 Eventuali disturbi sovrapposti a v2 o i2 nel caso di un doppio bipolo
bilaterale vengono trasferiti alla porta 1
 Nel caso di doppio bipolo unilaterale questi disturbi non possono
modificare v1 e i1
 Per un doppio bipolo bilaterale v1 e i1 variano al variare del carico
 Per un doppio bipolo unilaterale v1 e i1 sono indipendenti dal carico
● Il fatto che un doppio bipolo sia unilaterale spesso rappresenta una
situazione vantaggiosa (più semplice da gestire)
● In pratica, di solito non possibile fare in modo che il parametro r sia
esattamente zero, ma solo che sia molto piccolo rispetto al parametro f
57
Funzioni di rete
● La sorgente viene rappresentata mediante un circuito equivalente di
tipo Thévenin o Norton
● Il carico viene rappresentato mediante una resistenza equivalente
58
Funzioni di rete
● Equazioni della sorgente
v1  vS  RSi1
i1  iS  GSv1
● Equazioni del doppio bipolo
 v1   ri
v    r
 2  f
rr   i1 
 

ro  i2 
 i1   g i
i    g
 2  f
g r   v1 
 

g o  v2 
v1   hi
 i   h
 2  f
hr   i1 
 

ho  v2 
● Equazioni del carico
v2   RLi2
i2  GL v2
● Scelta la rappresentazione del doppio bipolo, le equazioni consentono
di ricavare le tensioni e le correnti alle porte
● Inoltre è possibile determinare delle funzioni di rete che esprimono le
relazioni tra le tensione e le correnti alle porte
● In seguito, come esempio, si farà uso della matrice ibrida, ma il procedimento può essere esteso facilmente alle altre rappresentazioni
59
Guadagno di corrente
v1  hi i1  hr v2
i2  hf i1  ho v2
v2   RLi2
● Combinando l’equazione del carico con la seconda equazione del doppio bipolo si ottiene la relazione tra le correnti di ingresso e di uscita
i2  hf i1  ho RLi2

i2 
 Il guadagno di corrente è
hf
i1
1  ho RL
Ai 
i2
hf

i1 1  ho RL
● In particolare se si annulla la resistenza di carico si ha
Ai cc 
i2
 hf
i1
60
Guadagno di tensione
v1  hi i1  hr v2
i2  hf i1  ho v2
i2  GL v2
● Eliminando i1 e i2 dalle equazioni si ottiene la relazione tra le tensioni di
ingresso e di uscita
 GL v2  hf i1  ho v2  i1  
ho  GL


h  GL
v2  v1    hi o
 hr v2
hf
hf


 Il guadagno di tensione è Av 
v2
hf
hf


H  hi GL
v1
hi ho  hr hf  hiGL
● In particolare nel funzionamento a vuoto si ha
Av 0  
hf
H
61
Resistenza di ingresso
v1  hi i1  hr v2
i2  hf i1  ho v2
v2   RLi2
● La resistenza di ingresso del doppio bipolo caricato si ottiene
eliminando i2 e v2 dalle equazioni
hf

hh R 
i1
v1  hi i1  hr RLi2   hi  r f L i1

1  ho RL
1  ho RL 

v
hh R
hh
Rin  1  hi  r f L  hi  r f
i1
1  ho RL
ho  GL
i2 

● In particolare a vuoto e in cortocircuito si ottiene, rispettivamente
Rin0 
v1
H
hh
 hi  r f 
i1
ho
ho
Rincc  hi
62
Guadagni di tensione e corrente riferiti al generatore
● Per calcolare i guadagni riferiti ai generatori si moltiplicano i guadagni
di tensione e di corrente riferiti alla porta 1 per i fattori di partizione che
legano, rispettivamente, vS a v1 e iS a i1
AV S 
v2 v1 v2
Rin


AV
vS vS v1 RS  Rin
AIS 
i2 i1 i2
Gin
AI


iS iS i1 GS  Gin
63
Equazione di uscita
v1  vS  RSi1
v1  hi i1  hr v2
i2  hf i1  ho v2
● Eliminando i1 e v1, si ottiene la relazione che lega la tensione e la
corrente alla porta 2
vS  RSi1  hii1  hr v2
i2 


hf
hh 
VS   ho  r f v2
hi  RS
hi  RS 

i1 
vS  hr v2
hi  RS

● A partire da questa relazione di possono ricavare i circuiti equivalenti di
Thévenin e Norton del bipolo ottenuto collegando la sorgente e il doppio
bipolo
64
Resistenza di uscita
● La resistenza di uscita si ottiene azzerando il generatore
vS  0

hr hf 
v2




i
h
v
R


2
2
o
out


hi  RS 
i2

VS  0

hh 
  ho  r f 
hi  RS 

1
● Nei casi particolari di RS  0 o GS  0 si ha rispettivamente
Routcc

hh
  ho  r f
hi

1

h
  i
H

Rout0 
1
ho
65
Tensione a vuoto
i2  0  v2  v20
● La tensione di uscita a vuoto si ottiene ponendo i2  0 nell’equazione
di uscita

hf
hh 
vS   ho  r f v20  0
hi  RS
hi  RS 


v20  
hf
vS
ho hi  hr hf  ho RS
● La relazione tra la tensione a vuoto e la tensione del generatore è
v20
hf

vS
H  ho RS
66
Tensione a vuoto
● Lo stesso risultato si può ottenere utilizzando la resistenza di ingresso
a vuoto per determinare v1 e quindi moltiplicando v1 per il guadagno di
tensione a vuoto
H
Rin 0
ho
hf
 hf 
vS
v20  vS
Av 0  vS


H
h
R
Rin 0  RG



H
H

o G
 RG 
ho
67
Corrente di cortocircuito
v2  0  i2  i2 cc
● La corrente di uscita in cortocircuito si ottiene ponendo v2  0
nell’equazione di uscita
i2 cc 
hf
hf
vS 
iS
1  hiGS
hi  RS
● La relazione tra la corrente di cortocircuito e la corrente iS è
i2 cc
hf

iS 1  hi GS
68
Corrente di cortocircuito
● Lo stesso risultato si può ottenere utilizzando la resistenza di ingresso
in cortocircuito per determinare i1 e quindi moltiplicando i1 per il
guadagno di corrente in cortocircuito
i2 cc  iS
RS
RS
hf
Aicc  iS
hf  iS
hf
1  hiGS
Rincc  RS
hi  RS
69
Circuiti equivalenti del doppio bipolo
● Dal punto di vista della sorgente, il doppio bipolo può essere
rappresentato da una resistenza equivalente Rin che, in generale,
dipende dalla resistenza di carico RL
● Dal punto di vista del carico, il doppio bipolo può essere rappresentato
mediante un circuito equivalente di tipo Thévenin o Norton, i cui
parametri, in generale, dipendono dalla resistenza del generatore RS
70
Funzioni di rete espresse con i parametri R, G e H
Av
Ai
Rin
Rout
v 20
vS
i2 cc
iS
R
rf RL
R  ri RL
rf

ro  RL
G
gf

g o  GL
g f GL
G  g i GL
rr
ri  r f
ro  RL

gg 
 g i  r f 
g o  GL 

1

gr gf 
 g o 

g
G

i
S 

gf

GRS  g o
gf
g i  GS
rr
ro  r f
ri  RS
rf
ri  RS
rf

RGS  ro
H
hf

H  hi GL
hf
1  ho RL
1
hi 
hr hf
ho  GL

hh 
 ho  r f 
hi  RS 

hf

H  hoGS
hf
1  hi GS
1
71
Funzioni di rete espresse con i parametri R, G e H
Av0
Aicc
R
rf
ri
r
 f
ro
Rin0
ri
Rincc
R
ro
Rout0
ro
Routcc
R
ri
G
g
 f
go
gf
gi
go
G
1
gi
gi
G
1
go
H
h
 f
H
hf
H
ho
hi
1
ho
hi
H
72
Resistenza caratteristica
● Il valore della resistenza di carico RL per cui risulta Rin RL è detto
resistenza caratteristica e viene indicato con R0
● Utilizzando le espressioni ricavate per Rin e imponendo Rin RL R0
si ottiene
(ri  ro )  (ri  ro ) 2  4rr rf

R0 
2
 ( g  g )  ( g  g )2  4g g
o
i
o
r f
 i
2

1

 

(H  1)  (H  1) 2  4hi ho

2ho
● Quando RL R0 si dice che il doppio bipolo è adattato
73
Doppi bipoli in cascata
● Nella pratica si presenta frequentemente il caso in cui un sistema è
costituito da più doppi bipoli collegati in cascata
● Le funzioni che descrivono il comportamento del doppio bipolo risultante
non sono legate in modo semplice alle funzioni di rete relative ai singoli
componenti
● Non è semplice ricavare come cambia il comportamento del sistema se
viene variata la sua configurazione (per es. se viene eliminato uno dei
moduli o ne viene aggiunto un altro)
74
Doppi bipoli in cascata
● In alcuni casi particolari il problema può essere semplificato
 Per esempio, se tutti i doppi bipoli hanno resistenza di ingresso
molto elevata e resistenza di uscita molto piccola il guadagno di
tensione complessivo è circa uguale al prodotto dei loro guadagni
a vuoto
 Questa situazione non è sempre facilmente realizzabile
(specialmente nel caso di doppi bipoli passivi)
● Se tutti i doppi bipoli hanno la stessa resistenza caratteristica
 il doppio bipolo risultante ha ancora la stessa resistenza
caratteristica
 in condizioni di adattamento il guadagno complessivo si ottiene
moltiplicando i guadagni dei singoli doppi bipoli
● Questa scelta trova numerose applicazioni pratiche
 Es. sistemi a 600  usati in telefonia, sistemi a 50  utilizzati a
radiofrequenza e per strumenti di misura
75
N-porte resistivi
● Componenti con 2N terminali che costituiscono N porte
 per ciascuna porta la corrente entrante in uno
dei terminali è uguale a quella uscente dall’altro
● Relazioni costitutive
f1 v1 ,  , v N , i1 ,  iN , t   0

f N v1 ,  , v N , i1 ,  iN , t   0
f1, ..., fN funzioni generiche

● Se il tempo non compare esplicitamente nelle
funzioni il componente è detto tempo-invariante
76
N-porte lineari tempo-invarianti
● Nel caso più generale le equazioni costitutive di un N-porte
lineare e tempo-invariante sono del tipo
a11v1    a1N v N  b11i1    b1N iN  0

a N 1v1    a NN v N  b11i1    bNN iN  0
● Queste equazioni possono essere scritte nella forma
Av  Bi  0
dove
 v1 
 i1 
 a11  a1N 
 b11  b1N 
v     i     A       Β      
v N 
iN 
a N 1  a NN 
bN 1  bNN 
77
Rappresentazioni di un N-porte lineare
● Parametri di resistenza
v  Ri
 v1 
v    
v N 
 i1 
i    
iN 
 r11  r1N 
R      
rN 1  rNN 
 i1 
i    
iN 
 g11  g1N 
G      
 g N 1  g NN 
● Parametri di conduttanza
i  Gv
 v1 
v    
v N 
● Se l’N-porte ammette entrambe le rappresentazioni, si ha
G  R 1
R  G 1
● Le altre possibili rappresentazioni sono dette ibride
78
Significato dei parametri di resistenza
rjk 
vj
ik
ih  0 h  k
Rapporto tra la tensione alla porta
j e la corrente alla porta k quando
tutte le porte diverse dalla k-esima
sono a vuoto
79
Significato dei parametri di conduttanza
g jk 
ij
vk
vh  0 h  k
Rapporto tra la corrente alla porta
j e la tensione alla porta k quando
tutte le porte diverse dalla k-esima
sono in cortocircuito
80
Reciprocità
● Si dice che un N-porte è reciproco se, dati due generici insiemi di
tensioni e correnti vk , ik e vk , ik (k =1,...,N) compatibili con le sue
equazioni caratteristiche, è verificata la relazione
N
N
 v i   vi
k 1
k k
k 1
k k
 Se il componente ammette la matrice di resistenza vale la
relazione
rjk  rkj
k  j
 Se il componente ammette la matrice di conduttanza vale la
relazione
g jk  g kj
k  j
81
Teorema di reciprocità
● Un N-porte ottenuto connettendo componenti resistivi reciproci è
reciproco
Dimostrazione
● Premessa: per un resistore la condizione di reciprocità è sempre
verificata, infatti
v  Ri
vi  Rii
 vi  vi

v  Ri
vi  Rii
● Si considerano due condizioni di funzionamento dell’N-porte, in cui le
porte vengono collegate a due insiemi arbitrari di N bipoli, scelti con
l’unico vincolo che i circuiti ottenuti dal collegamento ammettano
soluzione unica
● Si indica con l il numero totale di lati dei circuiti così ottenuti e si
attribuiscono i numeri da 1 a N ai bipoli collegati alle porte
82
Teorema di reciprocità
Dimostrazione
● Si indicano le tensioni e le correnti relative ai due funzionamenti con
v1,  , vl i1,  , il e v1,  , vl i1,  , il
● Per il teorema di Tellegen si ha
N
l
 v i   v i  0
k 1
k k
k  N 1
k k
N
l
 vi   vi  0
k 1
k k
k  N 1
k k
● Se l’N-porte è formato da componenti reciproci, i secondi addendi di
queste equazioni sono uguali
l
l
 v i   vi
k  N 1
k k
k  N 1
k k
 Questo richiede che siano uguali i primi addendi, cioè che le tensioni e
le correnti dell’N-polo risultante soddisfino la condizione di reciprocità
N
N
 v i   vi
k 1
k k
k 1
k k
83
N-porte dinamici
● Per una rete lineare dinamica a N porte le relazioni tra le correnti e le
tensioni alle porte sono di tipo differenziale lineare omogeneo
● In condizioni di regime sinusoidale, applicando la trasformata di
Steinmetz si ottengono relazioni lineari algebriche omogenee tra i fasori
delle tensioni V1...VN e delle correnti I1... IN del tipo
Av  Bi  0
dove
 V1 
 I1 
 a11  a1N 
 b11  b1N 
v     i     A       Β      
VN 
I N 
a N 1  a NN 
b N 1  b NN 
● Le equazioni hanno la stessa forma delle equazioni di un N-porte
resistivo, ma in questo caso le matrici hanno coefficienti complessi
dipendenti dalla pulsazione
84
Matrici di impedenza e di ammettenza
● Se il componente è comandato in corrente oppure in tensione è
possibile rappresentarlo mediante parametri di impedenza o di
ammettenza che costituiscono l’estensione al caso dei regimi
sinusoidale dei parametri di resistenza e di conduttanza
● Matrice di impedenza
v  Zi
 z11  z1N 
Z      
z N 1  z NN 
z jk 
Vj
Ik
I h  0 h  k
● Matrice di ammettenza
i  Yv
 y11  y1N 
Y      
y N 1  y NN 
y jk 
Ij
Vk
Vh  0 h  k
85
Matrici ibride e matrici di trasmissione
● Per i componenti a due porte si possono estendere al regime
sinusoidale le definizioni delle matrici ibride e di trasmissione
(in questo caso i coefficienti sono complessi e dipendono da )
 I1 
V1  h11 h12   I1 
H




V 
  
 I  h
 2
 2   21 h 22  V2 
Matrice ibrida
 h12
  V1 
V1 
 I1  h11

H




I 
V  h h   I 
22   2 
 2
 2   21
Matrice ibrida inversa
 V2 
V1   A B   V2 
T




 I 
 I   C D   I 
  2
 2
 1 
Matrice di trasmissione
 V1 
V2   A B  V1 

 I    C D   I   T   I 
  1
 1
 2 
Matrice di trasmissione inversa
86
Relazioni tra le rappresentazioni dei doppi bipoli
Z
Z
Y
z11
z12
z 21
z 22
z 22
Z

Y
z 21

Z
Z
z 22
H
z
 21
z 22
1
z11
H
z 21
z11
z11
z 21
T
1
z 21
z 22
z 21
T
1
z12
z12
Z
z11
Z
z12
z 22
1
z 22
z
 12
z11
Z
z11
Z
z 21
z 22
z 21
Z
z12
z11
z12

y 22
Y
y
 21
Y
y11
y 21
1
y11
y 21
y11
Y
y 22
y
 21
y 22
y
 22
y 21
Y

y 21
y
 11
y12
Y

y12
y
 12
Y
y11
Y
y12
y 22
y12
y11
Y
y11
y12
y 22
1
y 22
1

y 21
y
 11
y 21
1

y12
y
 11
y12

H
H h12
h 22
h 22
1
h 21

h 22 h 22
1
h
 12
h11
h11
h 21 H
h11
h11
h11
h12
h 21 h 22
h 22
h
 12
H
H
h
h11
 21
H H
h
H

 11
h 21
h 21
1
h
 22 
h 21
h 21
1
h11
h12 h12
h 22 H
h12 h12
H
1
h
 12


h11
h11
h21 H


h11
h11

H h12
h22
h22
1
h
 21
h22 h22
h22
h
 12
H
H

h
h11
 21
H H
 h12

h11
h21 h22
1
h21

h11
h21
H


h12

h11


h12
h22
h21
H
h21
h
 22

h12
1


h12
T
A T
C C
1
D
C C
D
T

B
B
1
A

B
B
B
T
D
D
1 C

D D
T
C

A
A
1
B
A
A
A B
C D
D
T
C
T
B
T
A
T
T
1
D
C C
T A
C C
1
A

B
B
T D

B
B

1
B
A
A
T C

A A
1
C


D
D
T A
D
D
D
B
T T
C
A
T T
A  B
C D
Μ  det(M )
Ogni riga riporta le espressioni dei coefficienti di una matrice in funzione
dei coefficienti delle matrici indicate nelle intestazioni delle colonne
87
Circuiti con doppi bipoli dinamici
● Facendo uso della trasformata di Steinmetz, nel caso di circuiti in
regime sinusoidale, o, più in generale, della trasformata di Fourier è
possibile estendere ai circuiti contenenti doppi bipoli dinamici tutti i
risultati ricavati per i doppi bipoli e per gli N-porte resistivi
● In particolare si possono generalizzare
 i circuiti equivalenti dei doppi bipoli
 i teoremi di rappresentazione dei doppi bipoli
 le relazioni relative ai collegamenti tra doppi bipoli
 il teorema di reciprocità
 le definizioni delle funzioni di rete, che in questo caso divengono
funzioni a valori complessi della pulsazione 
88
Funzioni di rete espresse con i parametri Z, Y e H
Av
Ai
Z in
Z out
V20
VS
I 2 cc
IS
Z
zf ZL
Z  z i Z L
zf

zo  ZL
Y
yf

y o  YL
y f YL
G  y i YL
zz
zi  r f
zo  ZL

yy 
 y i  r f 
y o  YL 

1

yryf 

 y o 
y
Y

i
S 

yf

YZS  y o
yf
y i  YS
zz
zo  r f
z i  ZS
zf
z i  ZS
zf

ZGS  z o
H
hf

H  h i YL
hf
1  hoZL
1
hi 
h rhf
h o  YL

hh 
 h o  r f 
h i  ZS 

hf

H  h o YS
hf
1  h i YS
1
89
Funzioni di rete espresse con i parametri Z, Y e H
A v0
A icc
Z
zf
zi
z
 f
zo
Z in0
zi
Z incc
Z
zo
Z out0
zo
Z outcc
Z
zi
Y
y
 f
yo
yf
yi
yo
Y
1
yi
yi
Y
1
yo
H
h
 f
H
hf
H
ho
hi
1
ho
hi
H
90