La fisica moderna

LA RADIAZIONE DI CORPO NERO.
LE DIFFICOLTÀ DELLA TEORIA CLASSICA.
Verso la fine del diciannovesimo secolo si era creata una situazione contraddittoria in relazione alla teoria della radiazione del corpo nero.
E' noto che un corpo caldo emette radiazione sotto forma di calore. Tale
radiazione consiste di onde elettromagnetiche di lunghezza d'onda maggiore
della radiazione visibile. Lo spettro dell'energia risulta essere continuo e
dipendente dalla temperatura. Si definisce "corpo nero" un corpo che assorbe
completamente tutte le radiazioni che lo colpiscono, o, viceversa, quando viene
riscaldato, si comporta come corpo perfettamente irradiante; esso ha pertanto
sia assorbività o potere assorbente che emissività o potere emissivo pari ad 1. Si
può dimostare con argomenti termodinamici che il rapporto tra emissività e
assorbività è lo stesso per tutti i corpi ad una data temperatura ed è uguale al
potere emissivo di un corpo nero alla stessa temperatura (legge di Kirchhoff).
Nessun corpo può quindi emettere energia radiante nell'unità di tempo in misura
maggiore di un corpo nero e, pertanto, il corpo nero è il più efficiente sia come
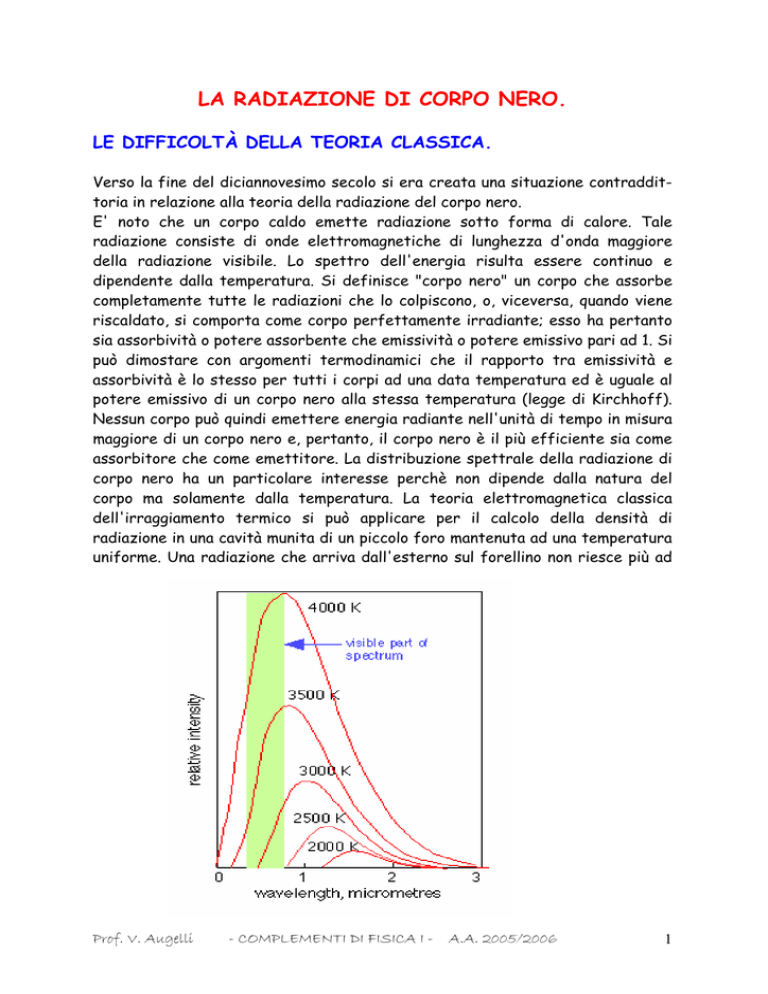
assorbitore che come emettitore. La distribuzione spettrale della radiazione di
corpo nero ha un particolare interesse perchè non dipende dalla natura del
corpo ma solamente dalla temperatura. La teoria elettromagnetica classica
dell'irraggiamento termico si può applicare per il calcolo della densità di
radiazione in una cavità munita di un piccolo foro mantenuta ad una temperatura
uniforme. Una radiazione che arriva dall'esterno sul forellino non riesce più ad
Prof. V. Augelli
- COMPLEMENTI DI FISICA I -
A.A. 2005/2006
1
uscire dall'involucro perciò il foro si comporta come un corpo nero. Tuttavia una
piccola quantità di radiazione uscirà e potrà essere spettroscopicamente
analizzata, ma non turberà l'equilibrio statistico. Un tale radiatore emetterà,
secondo la teoria classica, energia di radiazione di lunghezza d'onda variabile
con continuità ovvero gli atomi costituenti le pareti emetteranno e assorbiranno
radiazione elettromagnetica; in condizione di equilibrio, l'energia emessa
nell'unità di tempo sarà uguale a quella assorbita nello stesso tempo. Misure a
varie temperature, per mezzo di un bolometro, furono effettuate da Lummer e
Pringsheim (1899); le curve di radiazione furono misurate per temperature di
emissione differenti fra 1000 °C e 1650 °C. Essi trovarono che il massimo della
distribuzione aumentava con la temperatura e si spostava verso le lunghezze
d'onda più piccole.
Un approccio classico al problema della radiazione fu fatto da Wien nel 1893.
Egli trovò che l'energia radiante per unità di volume era una funzione del tipo:
⎛ ν ⎞⎟
⎝ T⎠
u(ν, T) = ν f ⎜
3
Per determinare il massimo della funzione, fissata T, poniamo uguale a zero la
derivata prima:
∂u
1 ⎛ ν⎞
⎡ ⎛ ν ⎞ ν ⎛ ν⎞ ⎤
⎛ ν⎞
= 0 = 3ν 2f ⎜ ⎟ + ν3 f' ⎜ ⎟ = ν2 ⎢ 3f ⎜ ⎟ + f' ⎜ ⎟ ⎥
⎝ T⎠
∂ν
T ⎝ T⎠
⎣ ⎝ T ⎠ T ⎝ T⎠ ⎦
Questa espressione si annulla per un certo valore di ν/T che sarà sempre lo
stesso se si varia ν e T, ma in maniera tale che il valore del loro rapporto non
cambi e soddisfi quindi la condizione di massimo. Wien trovò sperimentalmente
la legge dello spostamento:
λ maxT = cos t = 2.898 10-3 m K
(1)
Pertanto la frequenza a cui il massimo della distribuzione si ha è proporzionale
alla temperatura.
Un'altra legge importante è quella stabilita sperimentalmente da Stefan (1879)
e dimostrata teoricamente da Boltzmann (1884). Tale legge afferma che la
radianza totale, cioè la quantità di energia per unità di area e di tempo, RT, è
proporzionale alla quarta potenza della temperatura: RT = σT4. Essendo RT
proporzionale alla funzione u di Wien, possiamo scrivere:
∞
∞
⎛ν ⎞
RT = cos t ∫ ν f ⎜ ⎟dν = T 4 ∫ z 3 f ( z )dz = σT 4
⎝T ⎠
0
0
−8
−2 −4
La costante di Stefan vale: σ = 5. 67 ⋅ 10 Wm K .
3
(2)
Nel 1900 Rayleigh e, qualche anno dopo, Jeans ricavarono una formula che dà
l'energia di radiazione per unità di volume in equilibrio nella cavità, in un
intervallo di lunghezze d'onda che si estende fra λ e λ- dλ.
L'argomentazione procede come segue: la radiazione nella cavità deve esistere
come onde stazionarie aventi nodi sulle pareti metalliche della cavità; si
Prof. V. Augelli
- COMPLEMENTI DI FISICA I -
A.A. 2005/2006
2
determina il numero delle onde stazionarie di frequenze comprese tra ν e ν
+dν e come esso dipende da ν. L'energia che compete a ciascun onda (grado di
libertà) è nota dalla teoria statistica classica, quindi si può ricavare la densità
dell'energia della radiazione in un certo intervallo di frequenze.
Consideriamo una scatola cubica di lato a. La radiazione nella cavità subirà
riflessioni sulle pareti; essa può essere analizzata in termini delle sue tre
componenti lungo gli spigoli del cubo che quindi non si mischiano e possono
essere trattate separatamente. Riferiamoci alla componente x. Le componenti
incidente e riflessa sulla parete formano onde stazionarie il cui campo elettrico
è quindi parallelo alle pareti, ma in tal caso ci sarebbe un moto di cariche in un
conduttore che è equipotenziale; perciò deve essere sulle pareti nullo il campo
elettrico cioè ci dev'essere un nodo in x=0 e x=a. Analogamente nelle direzioni y
e z. Queste condizioni determinano delle limitazioni sulle possibili lunghezze
d'onda e quindi frequenze, che la radiazione può avere nella cavità.
Vogliamo contare quante onde stazionarie aventi frequenza tra ν e ν +dν sono
possibili.
Consideriamo la componente x dell'onda elettromagnetica stazionaria nella
cavità:
E(x, t) = E osin (2πx / λ)sin (2 πνt)
Tale onda ha un'ampiezza che varia sinusoidalmente nello spazio e
sinusoidalmente oscilla nel tempo. Nei punti nodali l'ampiezza si deve annullare e
quindi deve essere 2 πx / λ = nπ ovvero x = nλ/2, dove n è un numero intero.
Il numero di valori permessi di frequenza nell'intervallo compreso tra ν e ν +dν
sia N(ν)dν. E' evidente che tale numero dipende da dν e non da ν; esso sarà pari
a (2a/c)dν .
Se consideriamo che, per ciascuna frequenza, esistono due onde indipendenti,
una per ciascun stato possibile di polarizzazione. Perciò, relativamente alla
direzione x,
N(ν)dν = (4a/c)dν
Prof. V. Augelli
- COMPLEMENTI DI FISICA I -
A.A. 2005/2006
3
Estendiamo questo discorso al caso tridimensionale.
Ogni punto corrisponde ad una terna e quindi ad un'onda stazionaria. Essendo i
punti uniformemente distribuiti, il numero di punti compresi tra la sfera di
raggio r =
nx + ny + n z e r+dr sarà il volume dell'ottante del guscio sferico,
2
2
2
cioè:
1
1
4a 2 2 2a
4πa3 2
2
N (ν)dν = 4 πr dr = 4 π 2 ν
dν = 3 ν dν
c
c
c
8
8
Questo valore va moltiplicato per 2 per tener conto dei due stati di
polarizzazione, per cui si ha:
3
8πa
N (ν)dν = 3 ν2 dν
c
Che ν =
(3)
cr
si può facilmente dimostrare se si considera un'onda la cui
2a
direzione di propagazione forma gli angoli α, β, γ con gli assi di un sistema di
riferimento; se λ/2 è la distanza tra due piani nodali, la distanza dei nodi lungo
gli assi sarà:
λx / 2 =
λ/2
,
cos α
λy / 2 =
λ/2
,
cosβ
λz / 2 =
λ/2
cos γ
e quindi dovendo esserci nodi anche sulle pareti, deve aversi:
la=n1λ/2
Prof. V. Augelli
- COMPLEMENTI DI FISICA I -
A.A. 2005/2006
4
ma = n2λ/2,
na = n3λ/2,
dove n1, n2, n3 sono numeri interi e l, m, n sono i coseni direttori della direzione
della radiazione (solamente quando sono soddisfatte queste condizioni, gli
spigoli del cubo rimarranno permanentemente nodi di vibrazione). Quadrando e
sommando, otteniamo
a (l + m + n ) = λ ( n1 + n 2 + n3 ) / 4
2
2
2
1 +m +n = l,
2
2
2
2
2
2
2
(n1 + n2 + n 3 ) / a = 4 / λ = 4 ν / c
ν = (n12 + n22 + n 23 )1/ 2 c / 2a = r c / 2a
2
poiché
allora
quindi
2
2
2
2
2
2
2
dove ν è la frequenza e c la velocità della radiazione.
Il problema successivo è quello di valutare quanta energia è associata a ogni
onda stazionaria di data frequenza. Dall'elettromagnetismo sappiamo che
l'energia associata può variare da zero a infinito con continuità ed è
proporzionale al quadrato dell'ampiezza dell'onda. Essendo l'insieme delle onde
in equilibrio termico con la cavità a queste si applicano i risultati della teoria
cinetica classica e, in particolare, il principio di equipartizione dell'energia. (Nel
caso delle onde stazionarie c'è un solo grado di libertà, cioè, l'ampiezza del
campo elettrico).
Una vibrazione, o un treno d'onde, deve essere considerato come un sistema
dinamico nel quale l'energia cinetica media è uguale all'energia potenziale media,
entrambe essendo eguali a kT/2, dove k è la costante di Boltzmann e T la
temperatura assoluta. Perciò l'energia totale media associata è kT, valore
indipendente dalla frequenza dell'onda. Tenendo conto che a3=V, la densità di
energia totale per ogni modo di vibrazione nell’intervallo infinitesimo di
frequenza o lunghezza d’onda, è perciò
RT (ν )dν = RT (λ )dλ = 8πν2dνkT/c3 = 8πkTλ−4dλ.
Questa è la formula della radiazione secondo la meccanica classica di RayleighJeans.
Secondo tale espressione, l'energia irradiata (da un corpo nero) in un dato
campo di lunghezze d'onda dλ aumenta rapidamente col diminuire di λ e in
effetti tende all'infinito per lunghezze d'onda abbastanza piccole.
La curva di distribuzione della radiazione osservata sperimentalmente è in
completo disaccordo con questa conclusione. Inoltre, l'energia trasportata da
tutte le lunghezze d'onda (emissione continua) è
∞
RT = ∫ RT (λ )dλ = ∫ 8πkT λ − 4 dλ
0
dove λ varia da zero all'infinito. L'integrale è uguale a infinito per ogni valore di
T all'infuori di T nullo, il che, interpretato fisicamente, significa che l'energia
totale irradiata nell'unità di tempo per unità di area è infinita per tutte le
Prof. V. Augelli
- COMPLEMENTI DI FISICA I -
A.A. 2005/2006
5
temperature. E' chiaro che questa conclusione è completamente falsa. Entrambe
le conclusioni sono errate ed entrambe falliscono completamente nello spiegare
la dipendenza della radiazione dalla temperatura. Le osservazioni di Lummer e
Pringsheim sull'irraggiamento del corpo nero non obbediscono alla legge di
Rayleigh-Jeans e la legge di Stefan-Boltzmann, che è stata confermata
dall'esperienza, mostra che l'irraggiamento termico è proporzionale a T4.
In realtà la formula di Rayleigh-Jeans può interpretare le curve per valori di
λ sufficientemente grandi, ma per piccoli λ si ha evidentemente un netto
disaccordo. La quantità di energia irradiata ad una certa temperatura è
proporzionale a T , il che corrisponde alla legge di Stefan, e non è, naturalmente,
infinita.
4
Poiché la deduzione matematica della formula classica è priva di errori, la
contraddizione con l'esperienza può significare soltanto che le ipotesi
fondamentali impiegate per dedurre l'espressione sono errate.
DIFFICOLTÀ
SPECIFICI.
DELLA
TEORIA
CLASSICA
DEI
CALORI
Secondo la teoria cinetica, l'energia media di ogni grado di libertà di una
molecola di gas alla temperatura T è kT/2. In un gas monoatomico vi sono tre
gradi di libertà, in modo che l'energia totale media per ogni particella è 3kT/2.
Un solido si immagina costituito di atomi individuali, parzialmente legati ai loro
vicini, ma che tuttavia possono risuonare e vibrare del tutto liberamente quando
si somministri del calore. Se supponiamo vi siano N atomi in una grammomolecola, l'energia cinetica di oscillazione per questa quantità sarà 3kTN/2, che
equivale a 3RT/2 poiché k = R/N. L'energia potenziale media per ciascuna delle
Prof. V. Augelli
- COMPLEMENTI DI FISICA I -
A.A. 2005/2006
6
tre componenti di vibrazione sarà kT/2 per ogni particella (si può dimostrare
che l'energia potenziale media è eguale all'energia cinetica media). Quindi
l'energia totale è E=3RT. Per definizione, il calore specifico a volume costante è
(dE/dT)v = 3R. Da questo ragionamento consegue che i calori specifici di tutti i
solidi dovrebbero essere eguali e indipendenti dalla temperatura.
Il valore numerico di 3R è di 5,96 calorie per grammomolecola e questo
procedimento fu ritenuto una conferma teorica della primitiva legge di Dulong e
Petit, secondo la quale la capacità termica della grammomolecola nella maggior
parte degli elementi solidi è approssimativamente uguale a 6 cal. Tuttavia,
questa legge fallisce completamente quando viene applicata a elementi leggeri
come il carbonio, e viene meno, in generale, a basse temperature, poiché i calori
specifici tendono a zero al tendere della temperatura allo zero assoluto. Questo
fallimento non può essere spiegato dalla teoria classica dell'assorbimento
termico la quale richiede che un corpo possa assorbire calore continuamente in
quantità infinitamente piccole, in modo che di nuovo appare chiaramente che i
presupposti fondamentali del punto di vista classico sono errati.
LA TEORIA DEI QUANTI.
Che l'energia totale media associata a un grado di libertà sia kT si può
dimostrare partendo dai risultati della statistica classica e cioè: dato un insieme
di oscillatori non interagenti e in equilibrio termodinamico (come le onde
stazionarie nella cavità), un oscillatore ha una probabilità di avere energia
compresa tra E ed E+dE data da:
p( E)dE = C exp(− E / kT )dE
(legge di distribuzione di Boltzmann).
L'energia media associata al sistema sarà:
∞
E =
∫ E exp (−E / kT )dE
0
∞
= kT
(4)
∫ exp(−E / kT )dE
0
Il fallimento dei metodi classici nello spiegare le curve di radiazione e i risultati
sui calori specifici, portò alla condanna dei presupposti fondamentali della fisica
classica, e nel 1900 Planck propose una ipotesi rivoluzionaria con la quale egli
dedusse la vera legge dell'irraggiamento termico. Questa ipotesi, conosciuta
come teoria dei quanti, ha profondamente alterato l'intero panorama della
fisica, sviluppatasi alla fine del diciannovesimo secolo partendo dall'ipotesi della
continuità dell'energia. Il cambiamento radicale di Planck consistette
Prof. V. Augelli
- COMPLEMENTI DI FISICA I -
A.A. 2005/2006
7
nell'introduzione del concetto di atomicità del regno dell'energia. Egli fece
quattro ipotesi fondamentali, e cioè:
1) Un corpo nero contiene degli oscillatori armonici semplici che possono vibrare
con tutte le frequenze possibili.
2) La frequenza irradiata da un oscillatore è uguale alla frequenza
meccanica.
3)
L'emissione della radiazione ha luogo a intervalli discreti, e l'ampiezza rimane costante nei periodi di emissione.
4)
Un oscillatore che emette una frequenza ν può irradiare solamente
in unità, o quanti, di grandezza hν, dove h è una costante universale nota oggi
come costante di Planck.
Gli oscillatori possono essere considerati gli elettroni degli atomi che investiti
dalla radiazione elettromagnetica reirradiano energia elettromagnetica.
La quarta ipotesi è la più rivoluzionaria; essa suppone infatti che l'energia
possa essere irradiata solamente in quantità discrete, o pacchetti, e non in
quantità variabili con continuità.
Come Planck giunse alla formulazione di tali ipotesi. Osservando che la legge
di Rayleigh-Jeans funziona a basse frequenze, egli pensò che il punto debole
doveva essere l'uso del principio di equipartizione per cui questo andava bene a
basse frequenze, cioè,
E ⎯ν→0
⎯⎯→ kT
(5)
mentre, per qualche motivo, doveva essere
E ⎯ν→∞
⎯⎯→0
.
(6)
Tale risultato si ottiene se l'energia viene considerata come una variabile
discreta e non continua per cui gli integrali nella (4) diventano delle sommatorie.
LA TEORIA QUANTISTICA DELL'IRRAGGIAMENTO TERMICO.
Consideriamo un corpo nero che contenga una grande quantità di oscillatori
lineari che possono vibrare solamente per valori di energia interi ∆E . Dovendo
soddisfare alle condizioni (5) e (6) tale valore doveva dipendere
necessariamente dalla frequenza per cui ipotizzò la dipendenza più semplice,
cioè quella lineare: ∆E =hν. Gli oscillatori avranno quindi energie uniformemente
distribuite E= 0, hν, 2hν, 3hν,...,
Calcoliamo l'energia media degli oscillatori usando sempre la legge di
distribuzione di Boltzmann:
Prof. V. Augelli
- COMPLEMENTI DI FISICA I -
A.A. 2005/2006
8
∞
∑ nhν e− nhν/ kT
E =
n=0
∞
e quindi
∑
e
−nhν/ kT
n =0
hν ∑ nxn
=
n
∑x
n
hν ⋅ x ∑ nx n−1
=
n
∑ xn
n
n
E =
1
(1 − x )2
=
1
hν ⋅ x
1− x
1− x
hν ⋅ x ⋅
=
hν
e
hν/ kT
(7)
−1
dove si è usato x =exp(- hν/kT); nella terza uguaglianza la serie al numeratore è
la derivata della serie al denominatore.
Per ottenere la legge di distribuzione dell'energia di Planck, si deve moltiplicare
l'energia di ogni oscillatore per il numero effettivo degli oscillatori di data
frequenza contenuti nell'unità di volume. Il numero di oscillatori contenuti
−4
nell'intervallo di lunghezza d'onda λ → λ − dλ è eguale a 8π λ dλ quindi la
legge di distribuzione diviene
RT (λ )dλ = 8πhcλ −5 dλ /(exp(hc / kλT ) − 1)
(8)
dν
c
= RT (ν ) 2 se si vuole scrivere la
Si tenga conto che RT (λ ) = − RT (ν )
dλ
λ
legge in funzione della frequenza.
Quando λ è grande, o più precisamente quando hν è piccolo in confronto a kT, il
fattore
exp [hν/kT] - 1 tende a hv/kT
Dalla (7) si vede che in questo caso l'energia media E di un grado di libertà
diventa eguale a kT (indipendente dalla frequenza). Per questa ragione la legge
di distribuzione dedotta dalla teoria dei quanti darà lo stesso risultato numerico
di quella dedotta per via classica, quando si consideri una radiazione di grande
lunghezza d'onda.
Se la formula di Planck si scrive nella forma
RT (ν )dν = (8πkTλ −4 dλ ) ⋅ (hν / kT ) /(exp(hν / kT ) − 1)
il primo termine fra parentesi equivale alla formula di Rayleigh-Jeans, per cui si
può concludere che la formula della teoria dei quanti si può ottenere dalla
formula
classica
moltiplicando
questa
ultima
per
il
fattore
(hν / kT ) / (exp(hν / kT ) − 1) , che si può chiamare il fattore di moltiplicazione
di Planck.
Possiamo ricavare la legge di Wien e quella di Stefan dalla legge di Planck che
riscriviamo come:
RT (λ ) = 8πhcλ −5 /(exp(hc / kλT ) − 1)
Per trovare il massimo della distribuzione imponiamo d ( RT (λ )) / dλ = 0 . Tale
condizione conduce ad una equazione esponenziale che si risolve con
Prof. V. Augelli
- COMPLEMENTI DI FISICA I -
A.A. 2005/2006
9
approssimazioni successive. Si trova che λmaxT=0,298. La densità totale di energia
è data da:
∞
RT = ∫ RT (ν )dν =
0
8πh
c
3
∞
ν 3 dν
∫ e hν / kT
0
8πh ⎛ kT ⎞
= 3 ⎜ ⎟
−1 c ⎝ h ⎠
4∞
x 3 dx
∫ e x − 1 = σT
4
0
dove x=hν/kT. Valutando l'integrale si trova per σ il valore 7.564 10-16 Jm-3K-4.
Da ciò si vede come la teoria dei quanti, relativa all'irraggiamento termico,
abbia avuto un completo successo dove invece la teoria classica era fallita.
Perciò ci si poteva attendere che le considerazioni basate sulla teoria dei quanti
conducessero a una soluzione delle difficoltà relative ai calori specifici. Tale
previsione fu confermata.
L'EFFETTO FOTOELETTRICO.
Tra il 1886 e il 1887 Hertz eseguì alcuni esperimenti con i quali confermò
l'esistenza delle onde elettromagnetiche e la validità dell'elettromagnetismo di
Maxwell. Inoltre, Hertz scoprì che una scarica elettrica tra due elettrodi
avviene più facilmente se si illuminano gli elettrodi con luce ultravioletta. Tale
fenomeno è noto come effetto fotoelettrico e, in generale, consiste nel fatto
che se superfici metalliche sono colpite dalla luce o da raggi X, vengono emessi
elettroni dai metalli.
L'apparato sperimentale è schematicamente rappresentato in figura.
vetro
A
quarzo
B
luce
incidente
V
G
inversione di
polarità
Nel recipiente di vetro è stato praticato il vuoto. La luce di data frequenza
incide sulla piastra metallica A che emette elettroni (fotoelettroni). Applicando
una differenza di potenziale V tra A e B, con B positivo, si misura con G una
corrente. La dipendenza della fotocorrente da V è quella in figura.
Prof. V. Augelli
- COMPLEMENTI DI FISICA I -
A.A. 2005/2006
10
i
a
b
0
V
V
o
Prof. V. Augelli
- COMPLEMENTI DI FISICA I -
A.A. 2005/2006
11
Quando V è sufficientemente alto la corrente giunge alla saturazione, cioè tutti
i fotoelettroni sono raccolti da B. Se invertiamo il segno di V, la corrente non va
subito a zero, ciò vuol dire che i fotoelettroni sono emessi con una certa energia
cinetica; se questa è sufficiente alcuni fotoelettroni raggiungeranno B
nonostante il campo avverso. La corrente si annulla per un certo valore del
potenziale ritardante che sarà pertanto legato all'energia cinetica massima:
Kmax=eVo
Se si varia l'intensità luminosa, come per esempio in b), Vo è lo stesso e quindi la
energia cinetica massima non dipende dall'intensità luminosa. Se invece, si varia
la frequenza della luce incidente si trova la una dipendenza lineare tra Vo e ν (la
figura si riferisce a luce sul sodio).
V
o
(V)
2
1
4
νo
14
8
12 x 10
Hz
Come si osserva, esiste una frequenza di soglia al di sotto della quale non si
osserva effetto fotoelettrico.
Perciò, per qualsiasi superficie, irradiata con luce di frequenze differenti, si è
trovato che l'energia cinetica degli elettroni emessi non dipende dalla intensità
della luce, ma varia linearmente con la frequenza.
Da un punto di vista classico tale fenomeno è totalmente incomprensibile.
Infatti, in termini di teoria ondulatoria,
a) una variazione di intensità luminosa cambia l'ampiezza del campo elettrico e
quindi la forza agente sull'elettrone e conseguentemente la sua energia cinetica.
Ma ciò non si osserva: l'energia cinetica risulta indipendente dalla intensità
luminosa.
b) Da un punto di vista classico, l'effetto dovrebbe essere osservato una volta
che l'intensità è sufficientemente elevata da fornire sufficiente energia per
estrarre i fotoelettroni, perciò l'effetto non dovrebbe dipendere dalla
frequenza. Ma si osserva una frequenza di soglia al di sotto della quale non si
osserva l'effetto qualunque sia l'intensità.
c) Classicamente l'energia è uniformemente distribuita sul fronte d'onda. Se
l'intensità è bassa, l'interazione fronte d'onda - elettrone trasferirebbe una
piccolissima quantità di energia per cui il tempo necessario per osservare
l'effetto, diminuendo l'intensità, dovrebbe aumentare perchè sarebbe
Prof. V. Augelli
- COMPLEMENTI DI FISICA I -
A.A. 2005/2006
12
necessario più tempo all'elettrone per accumulare l'energia sufficiente per
fuoriuscire dal metallo. Tale ritardo di tempo non si osserva. Alcuni esperimenti
eseguiti con debolissimi raggi di luce mostrarono che l'effetto fotoelettrico ha
inizio non appena il metallo viene irradiato (o almeno entro 3 x l0-9 secondi).
Per spiegare questi fatti sperimentali Einstein nel 1905, propose una estensione
delle idee di Planck sulla quantizzazione dell'energia degli elettroni irradianti in
una cavità. Egli assunse che l'energia portata da un'onda luminosa non fosse
uniformemente distribuita sul fronte d'onda, ma localizzata in piccole regioni. Il
contenuto energetico di un'onda elettromagnetica di frequenza ν emessa da una
sorgente può essere 0, hν , ...., nhν ; per passare da un contenuto energetico ad
un altro (vicino) è necessario emettere o assorbire una quantità di energia pari
ad hν. Einstein assunse che tale quantità era localizzata in un pacchetto che si
chiamerà fotone. In termini di fotone l'effetto fotoelettrico può essere
completamente spiegato.
Se W è la quantità di lavoro necessario per estrarre l'elettrone dal metallo
(esso varia da sostanza a sostanza), l'energia cinetica con cui un elettrone è
emesso sarà data da
K = hν -W
Per gli elettroni meno fortemente legati che non perdono energia per collisioni
all'interno dell'atomo, il lavoro necessario per estrarre un elettrone è detto
lavoro di estrazione, W ; in tal caso, l'energia cinetica con cui l'elettrone
fuoriesce è massima:
(8)
Kmax = hν - Wo
Vediamo come il concetto di fotone supera le difficoltà incontrate dalla teoria
classica.
Variare l'intensità luminosa significa variare il numero di fotoni e quindi varierà
il numero totale degli elettroni emessi.
L'esistenza di una frequenza di soglia discende dalla (8) se poniamo Kmax = 0, per
cui
νo=Wo /h
Se i fotoni non hanno energia almeno pari ad hνo la corrente sarà zero
indipendentemente dal numero di fotoni.
L’introduzione del concetto di fotone elimina anche il problema del ritardo
temporale in quanto l’intero quanto è scambiato in un singolo atto di interazione:
se un fotone urta un atomo, esso viene assorbito e un elettrone viene emesso. La
(8) può essere scritta:
eVo = hν − Wo
cioè esiste una relazione lineare tra potenziale ritardante e frequenza; la
pendenza della retta è h/e.
Si vede cosi che l'effetto fotoelettrico fornisce una prova decisiva a sostegno
della teoria dei quanti e suggerisce l'idea di una estensione della ipotesi di
Prof. V. Augelli
- COMPLEMENTI DI FISICA I -
A.A. 2005/2006
13
Planck. Poiché l'energia non è solamente irradiata in quantità discrete, ma
queste quantità individuali viaggiano come pacchetti separati di energia
piuttosto che sotto forma di vibrazioni propagantisi come onde. L'assorbimento
di un quanto di radiazione si può ora comprendere più facilmente, perché
l'energia radiante urta contro una superficie assorbente sotto la forma di una
pioggia di quanti ed evidentemente deve essere assorbita in quantità intere.
EFFETTO COMPTON.
Le idee quantistiche di Planck e Einstein furono successivamente applicate
per spiegare l'effetto Compton (1923). Compton osservò che quando la
radiazione x interagiva con la materia si osservava una radiazione diffusa avente
una frequenza minore di quella della radiazione incidente.
Egli osservò, inoltre, che la frequenza della radiazione diffusa dipendeva dalla
direzione di diffusione (o scattering). Analizzando la radiazione diffusa per
mezzo di uno spettroscopio si trovava che tale radiazione di frequenza ν' < νinc
aveva intensità anche maggiore di quella del fascio incidente se il materiale
aveva un basso numero atomico (C, Al) e il fascio incidente era "duro" (alte
frequenze) oppure l'intensità risultava minore se il materiale aveva un alto
numero atomico (Pb) e il fascio incidente era "molle" (basse frequenze).
Gli spettri misurati da Compton usando raggi x su grafite sono riportati in figura
per vari angoli di diffusione. La prima linea verticale è la lunghezza d'onda dei
raggi incidenti.
L'apparato sperimentale era costituito da una sorgente di raggi x, un target di
grafite, un rivelatore (camera di ionizzazione) che misura le intensità relative
alle varie lunghezze d'onda dei raggi x diffusi e separate dalle riflessioni alla
Bragg su un cristallo.
Il comportamento degli spettri osservati veniva correttamente descritto dalla
relazione:
λ' − λ = 0. 024(1 − cos θ)
(9)
dove λ e λ sono le lunghezze d'onda, espresse in Å, della radiazione incidente e
diffusa, rispettivamente, e θ è l'angolo di diffusione.
Da un punto di vista classico, la teoria di Maxwell-Lorentz prevede che gli
elettroni investiti dal campo elettrico oscillante della radiazione incidente
producono delle oscillazioni forzate. Essendo gli elettroni accelerati nella
direzione di propagazione dell'onda elettromagnetica, essi dovrebbero
'
Prof. V. Augelli
- COMPLEMENTI DI FISICA I -
A.A. 2005/2006
14
sorgente
collimatori
cristallo
x
incidenti
x diffusi
target
θ
rivelatore
emettere una radiazione di frequenza uguale a quella del campo
elettromagnetico se non si sovrapponesse l'effetto Doppler1. Tale effetto
costringe l'elettrone oscillante ad emettere anche un'altra frequenza ν' , la cui
dipendenza dall'angolo di osservazione è:
λ' − λ = λ
v
(1 − cosθ )
c
dove v è la velocità dell'elettrone. Lo sdoppiamento della frequenza sarebbe
dovuto aumentare con l'energia ceduta dalla radiazione agli atomi, ma ciò non si
osservava.
Compton fece l'ipotesi che l'interazione della radiazione con la materia fosse
riconducibile ad un urto elastico tra fotone ('quanto' del campo
elettromagnetico) ed elettrone.
1La
legge di assorbimento e riemissione alla stessa frequenza è valida nel sistema di riferimento in
cui l'elettrone è a riposo. Nel sistema laboratorio c'è anche l'effetto Doppler.
Prof. V. Augelli
- COMPLEMENTI DI FISICA I -
A.A. 2005/2006
15
Con riferimento alla figura, supponiamorl'elettrone inizialmente fermo in O e il
fotone incidente con quantità di moto p . Applichiamo le leggi di conservazione
per l'urto elastico:
p
e
ϕ
p
O
p'
θ
r r r
p = p' + pe
(10)
E + me c 2 = E' +c m2e c2 + p 2e
(11)
r
r r
Dalla (10): pe = p − p' , quadrando:
2
2
r r ⎛ hν ⎞
hν hν'
⎛ hν' ⎞
2
2
2
⎟ −2
pe = p + p' −2 p ⋅ p ' = ⎜ ⎟ + ⎜
cosθ (12)
⎝ c ⎠
⎝ c ⎠
c c
2 1
2
2
2 2
Dalla (11): pe = E + me c − E'
2 − me c
c
[(
)]
Confrontando la (11) e la (12) e tenendo conto che E=hν e E'=hν', si ha:
[(E + m c
2
e
− E'
)]
2
2
2
1
E E'
⎛ E⎞
⎛ E' ⎞
2 2
⎟ +⎜ ⎟ −2
cos θ
2 − m ec = ⎜
⎝c⎠
⎝ c⎠
c
c c
da cui
E − E' =
ed essendo E = hν =
1
(1 − cos θ)EE'
m e c2
hc
si ottiene:
λ
λ' − λ =
La quantità
h
(1 − cosθ )
m ec
(13)
h
= λ C = 0. 024 Å è nota come lunghezza d'onda Compton.
m ec
La (13) è in ottimo accordo con i dati sperimentali. Come si vede dalla (13) lo
shift Compton, ∆λ, dipende solo dall’angolo di scattering e non dalla lunghezza
d’onda della radiazione incidente; ∆λ varia da 0 per θ=0 a 2λC per θ=180° . La
differenza essenziale tra punto di vista classico e quantistico è nel fatto che il
primo prevede un trasferimento continuo di energia e impulso dalla radiazione a
tutti gli elettroni ad essa sottoposti, mentre il secondo assume un
trasferimento di energia discontinuo e praticamente istantaneo ad alcuni
elettroni.
Verifiche sperimentali della teoria dell'effetto Compton furono fatte nel
1925 da Bothe e Geiger che rivelarono la presenza di elettroni di rinculo tramite
contatori e da Compton e Simon che rivelarono elettroni di rinculo in una camera
Prof. V. Augelli
- COMPLEMENTI DI FISICA I -
A.A. 2005/2006
16
di Wilson. L'analisi di questi esperimenti permise di stabilire che si trattava
proprio di un urto fotone-elettrone. Per individuare gli elettroni di rinculo
prodotti per effetto Compton, bisogna escludere dall'analisi quelli prodotti per
effetto fotoelettrico. Questi ultimi acquistano una energia pari a hν-W ≅ hν
essendo W piccolo rispetto ad hν, per cui tutti faranno in media lo stesso
percorso se la radiazione incidente è monocromatica; gli elettroni Compton
avranno velocità minori perchè minore è l'energia da essi assorbita e quindi i
cammini saranno sempre più brevi per θ crescenti. Per determinare l'angolo di
diffusione dell'elettrone si considera la tangente nell'origine della traiettoria,
mentre per determinare l'angolo del fotone diffuso si considera la traccia
dell'elettrone di rinculo creato dal fotone diffuso.
E’ necessario, tuttavia, spiegare la presenza del picco avente la stessa λ del
fotone incidente. La (13) è stata ricavata assumendo libero l’elettrone con cui il
fotone interagisce. Se l’energia di legame dell’elettrone al proprio atomo è
piccola rispetto all’energia cinetica che esso acquista per effetto dell’urto con il
fotone, l’ipotesi di elettrone libero va ancora bene. Ma se i valori dell’energia del
fotone incidente e/o l’energia di legame dell’elettrone sono tali per cui l’urto non
libera l’elettrone, l’interazione può essere riguardata come tra fotone e atomo.
Allora nella (13) possiamo porre M, massa dell’atomo, invece di m0, massa
dell’elettrone per cui ∆λ risulta essere molto piccolo e il fotone diffuso ha
praticamente la stessa lunghezza d’onda del fotone incidente. Questo tipo di
processo è noto come scattering Rayleigh. L'esperimento di Simon e Compton
del 1925 stabilì in maniera inequivocabile la natura corpuscolare della radiazione
elettromagnetica. Essi osservarono gli effetti dell'interazione tra raggi x e una
lastrina di un materiale in una camera a nebbia. L'elettrone urtato lasciava una
traccia nella camera con una curvatura generata da un campo magnetico
opportuno. Ciò permetteva di misurare l'impulso e quindi l'angolo di diffusione
del fotone usando le leggi di conservazione.
Prof. V. Augelli
- COMPLEMENTI DI FISICA I -
A.A. 2005/2006
17
MODELLI ATOMICI.
MODELLO ATOMICO DI THOMSON.
Molti fatti sperimentali accumulati sino al 1910 (effetto fotoelettrico,
scattering di raggi x da parte di atomi, ....) avevano stabilito l'esistenza degli
elettroni all'interno dell'atomo. Si era anche cercato di capire quanti elettroni
ci fossero nell'atomo e si era trovato che tale numero era A/2=Z, cioè, la metà
del peso atomico. Dovendo l'atomo essere neutro, era evidente che esso doveva
contenere una uguale, ma opposta, quantità di carica, cioè, +Ze. Essendo la
massa dell'elettrone molto più piccola di quella dell'atomo, la maggior parte
della massa dell'atomo doveva essere legata alla carica positiva. Il problema che
sorgeva era come la carica, negativa e positiva, era distribuita nell'atomo.
Thomson propose un modello secondo il quale l'atomo era costituito da una
distribuzione continua di carica positiva di forma sferica, entro la quale gli
elettroni erano disseminati come semi in un'anguria (o uvetta in un panettone!) in
maniera da neutralizzarla.
IL MODELLO DI RUTHERFORD.
L'inadeguatezza di questo modello fu dimostrata da Rutherford che nel 1911
effettuò degli esperimenti di scattering di particelle alfa da parte di atomi di
varie sostanze. Altri dati erano già disponibili: Geiger e Mardsen (1909) usarono
particelle alfa con velocità di 2 107 m/s sparate su fogli di oro di 40 microns. La
maggior parte delle particelle alfa attraversavano il foglio (e ciò era spiegabile
col modello di Thomson); quelle che subivano grosse deviazioni non interagivano
tanto fortemente con gli elettroni che avevano una massa molto minore
(1/7500): un urto centrale non cambierebbe la velocità di più dello 0.01%. Un
rinculo può solo essere giustificato da un urto con una particella massiva che
esercita quindi una forza considerevole, ma bisogna tener conto anche della
carica. Le particelle alfa venivano prodotte da una sostanza radioattiva
contenuta in un blocco di piombo. Le particelle attraversano una regione in cui è
Prof. V. Augelli
- COMPLEMENTI DI FISICA I -
A.A. 2005/2006
18
stato fatto il vuoto, colpiscono un sottile foglio di oro e vengono osservate dopo
la diffusione a vari angoli osservando con un microscopio il piccolo lampo
luminoso provocato dall'urto della particella su un rivelatore di solfuro di zinco.
Il modello di Thomson non poteva spiegare deviazioni così grandi perché le forze
esercitate sulla particella alfa dalla carica negativa e da quella positiva
avrebbero potuto produrre deviazioni al più di 1°, mentre si osservavano
particelle deflesse anche ad angoli maggiori di 120°.
Se si studia l'interazione particella alfa - sfera di carica positiva delle
dimensioni dell'atomo (10-8 cm), si trova che l'angolo di massima deviazione
della particella alfa è inversamente proporzionale al raggio della sfera carica;
quest'angolo risultava essere molto piccolo, come già detto. Rutherford pensò
allora che per aumentare tale angolo era necessario considerare una sfera di
raggio molto minore e quindi pensò ad un modello dell'atomo costituito da un
nucleo centrale carico positivamente con gli elettroni che ruotano intorno sotto
l'azione di forze elettromagnetiche. E' evidente che gli elettroni aventi una
massa molto più piccola delle particelle alfa non produrranno grosse deflessioni.
Considerando un sottile foglio di spessore t, Rutherford, sulla base del suo
modello atomico, calcolò che la frazione di alfa diffuse di un angolo φ risultava
essere proporzionale a a)
v −4
α .
[sin (φ / 2 ) ] −4 , b) a t, c) alla carica del nucleo e d) a
Tali predizioni trovarono conferma sperimentale da parte di Geiger e
Marsden che usando fogli di argento e oro trovarono un range angolare
compreso tra 5° e 150°.
Cambiando il tipo di materiale, la sorgente e l'angolo di osservazione le
previsioni a), b) e d) di Rutherford risultavano tutte confermate; l'effetto della
carica nucleare non risultava evidente. D'altra parte, era possibile calcolare dai
dati sperimentali la carica nucleare e ciò che si trovò fu 6e per il carbonio, 13e
o 14e per l'alluminio, ecc, cioè 1/2(peso atomico) x e. Ciò voleva anche dire che
intorno al nucleo vi doveva essere un numero di elettroni pari a 1/2(peso
atomico) affinchè il sistema fosse elettricamente neutro. Ciò portava in modo
quasi automatico a considerare l'atomo come costituito da un nucleo con carica
positiva pari al numero atomico Z e con Z elettroni orbitanti. Gli esperimenti
permisero a Rutherford di valutare le dimensioni del nucleo assumendo che la
legge di Coulomb poteva valere sino ad una distanza massima della particella alfa
Prof. V. Augelli
- COMPLEMENTI DI FISICA I -
A.A. 2005/2006
19
dal centro del nucleo pari alla somma dei loro raggi (cioè, non ci doveva essere
una deformazione del nucleo); la traiettoria da considerare è AB in figura per
cui r è la distanza di massimo avvicinamento.
In B l'energia cinetica iniziale è uguale all'energia potenziale elettrica (nucleo e
particella si respingono), per cui risulta:
1
k( Ze)(2e)
m α v 2α =
r
2
9
−12
Per fogli di oro e v α = 2 ⋅10 cm / s , si trova r = 3⋅10
cm da confrontare
−8
con le dimensioni dell'atomo ( ≈ 10 cm ). Si era spinti a supporre che le
dimensioni dell'atomo fossero determinate dalla presenza degli elettroni a
distanze relativamente grandi dal nucleo. Questa visione di un atomo vuoto
sosteneva la facilità con cui esso penetrava attraverso migliaia di strati atomici
dei fogli metallici. Il modello appena costruito pose subito tre domande: a) quale
è la struttura del nucleo? b) cosa tiene insieme il nucleo se le cariche che lo
costituiscono sono dello stesso segno? c)come sono disposti gli elettroni intorno
al nucleo? Alla terza domanda, Bohr diede presto risposta; per le altre due si
dovette attendere ancora!
Spettri continui di emissione della radiazione.
Gli spettri ottenuti analizzando la luce emessa da solidi e liquidi ad alta
temperatura come metallo fuso o elettrodi di carbone di un arco voltaico
avevano in comune tre caratteristiche:
a) dalla regione dell'IR all'UV, gli spettri sono continui;
b) solidi o liquidi emettono praticamente la stessa luce se alla stessa
temperatura, indipendentemente dalla natura chimica della sostanza.
Un carbone che ad una certa temperatura, emette luce rossa, in realtà emette
anche tutti gli altri colori, solo che il rosso è più intenso e se in una fornace con
tali carboni infiliamo un'asta di ferro, quando questa avrà raggiunto la stessa
temperatura dei carboni, essa emetterà la stessa luce rossa. Sperimentalmente
si tratterà di misurare la lunghezza d'onda della luce emessa tramite, per
esempio, un reticolo di diffrazione.
Il contributo energetico allo spettro da parte delle varie lunghezze d'onda può
essere misurato. Nell'intervallo dell'infrarosso, l'energia può essere misurata
con dispositivi misuratori di calore come termopile o bolometri. Nella regione
visibile e ultravioletta, l'energia può essere misurata con fotocelle o pellicole
fotografiche. Nel caso dello spettro della luce emessa dalla superficie del sole,
Prof. V. Augelli
- COMPLEMENTI DI FISICA I -
A.A. 2005/2006
20
l'energia è bassa nell'intervallo delle corte lunghezze d'onda, il picco è intorno
al colore verde e la maggior parte dell'energia è nella regione infrarossa. Ciò
che noi vediamo è la sovrapposizione dei colori della regione del visibile, che
costituisce la luce bianca. La cosa importante è che corpi chimicamente diversi
alla stessa temperatura hanno praticamente lo stesso spettro della luce emessa.
Se si considera la λ picco del sole, per la legge dello spostamento di Wien, si
ottiene una temperatura di 5300 K, ma se si tiene conto che parte dell'energia
è assorbita dall'atmosfera e che il sole non è un perfetto emettitore, si ottiene
T=6000 K per la superficie del sole. Con la stessa legge, la temperatura della
stella Vega è 14000 K, mentre per le stelle rosse come Antares si ha 2500 K.
Spettri a righe.
Abbiamo visto che gli spettri della radiazione emessa da corpi incandescenti
portarono Planck all'idea dei quanti. Tali spettri risultano dipendere solamente
dalla temperatura ed sono indipendenti dalla natura chimica della sostanza;
inoltre, essi sono continui, cioè interessano una regione continua di lunghezze
d'onda. Quando si osserva, invece, lo spettro della luce emessa da gas o vapori
quando vengono eccitati da una scintilla o da un arco voltaico, esso risulta essere
costituito da linee discrete.
Le linee non sono, in generale, equispaziate e alcune sono più luminose di altre;
inoltre, lo spettro dipende dal tipo di sostanza. Vapori di ferro mostrano circa
6000 linee, mentre vapori di sodio mostrano due linee gialle vicine e luminose. Il
fatto che lo spettro dei vapori delle sostanze fosse caratteristico delle
sostanze stesse incoraggiò lo sviluppo della spettroscopia e sviluppò l'analisi
chimica.
Nel 1814, Fraunhofer analizzò lo spettro continuo della luce solare tramite un
sistema a prismi; si vide che in realtà lo spettro non era continuo, ma vi erano
circa 700 linee scure (righe di assorbimento) e alcune di queste le osservò
anche nello spettro della luce di alcune stelle. Successivamente Kirchhoff notò
che lo spettro di corpi incandescenti era continuo, ma se la luce proveniente dal
corpo incandescente, prima di attraversare il prisma, passava attraverso vapori,
per esempio, di sodio, si notava nello spettro la presenza di una linea nera
corrispondente ad una linea presente nello spettro di Fraunhofer. Più
precisamente, le linee di assorbimento delle sostanze gassose che risultano
mancanti nello spettro della luce che le attraversa corrispondono alle linee di
emissione delle stesse sostanze gassose. Le linee nere nello spettro di
Prof. V. Augelli
- COMPLEMENTI DI FISICA I -
A.A. 2005/2006
21
Fraunhofer evidenziano quindi la presenza di elementi specifici nell'atmosfera
solare. Nella zona verde dello spettro solare si osservò una linea che non era
stata mai osservata negli spettri di emissione degli elementi allora noti; a tale
gas presente nell'atmosfera del sole fu dato il nome "elio". Tale gas fu
individuato sulla terra molto dopo.
Le difficoltà incontrate per spiegare gli spettri continui aumentano nel caso
degli spettri discreti. Abbiamo detto che gli spettri continui delle sostanze
solide o liquide non differiscono da una sostanza ad un'altra; questo potrebbe
essere spiegato pensando che la frequenza dell'atomo oscillatore individuale
viene mascherata a causa dei numerosi urti tra di essi. Tuttavia un gas rarefatto
in un tubo a incandescenza mostra comunque uno spettro a righe anche se gli
atomi si urtano tantissime volte. Un'altra complicazione riguardava la sequenza
delle righe dello spettro e il numero di righe di assorbimento che sembrava
dipendere dall'intensità della scarica.
Un tipico apparato sperimentale per misurare gli spettri atomici consiste di una
sorgente costituita da una scarica elettrica che attraversa una regione in cui
c'è un gas monoatomico. Alcuni atomi, a causa degli urti, passano in uno stato
eccitato e a seguito del processo inverso di diseccitazione l'atomo emette onde
elettromagnetiche che attraversano un prisma e finisce su una lastra
fotografica.
I solidi danno luogo a spettri continui, atomi liberi danno luogo a spettri discreti.
Per oltre venti anni, gli studiosi cercarono una qualche chiave matematica che
rendesse conto della sequenza di tali linee. Nel 1885, Balmer pubblicò un
articolo sullo spettro dell'idrogeno sulla base delle misure di lunghezza d'onda
effettuate da Ångstroem. Le quattro linee dell'idrogeno erano comunemente
note come, H α (rosso), H β (verde), H γ (blu), H δ (violetto). Balmer (1885)
trovò la seguente relazione
Prof. V. Augelli
- COMPLEMENTI DI FISICA I -
A.A. 2005/2006
22
⎛ n2 ⎞
λ (m) = C × ⎜ 2
⎟
⎝ n − 22 ⎠
dove C è una costante che vale 3645.6 10-10 m, n è un numero intero che vale 3
per H α , 4 per H β , 5 per H γ e 6 per H δ . L'accordo con i dati sperimentali era
entro lo 0.02%. Ponendo n=7, Balmer poteva prevedere la lunghezza d'onda di
una eventuale quinta riga, cioè H ε =3969.65 Å. In realtà, non solo tale riga fu
trovata poco tempo dopo, ma una serie di nove linee nella regione
dell'ultravioletto furono osservate e le lunghezze d'onda erano tutte previste
dalla formula di Balmer che riscriviamo nella forma più nota:
1 ⎞
1
⎛ 1
= R⎜ 2 − 2 ⎟
⎝2
n ⎠
λ
(1)
essendo R = 1.09678 107 m-1 la costante di Rydberg. Balmer, senza alcun
fondamento fisico, predisse che probabilmente poteva esistere serie le cui
lunghezze d'onda poteva essere previste da relazioni simili alla precedente, del
tipo
1
⎛ 1
1 ⎞
= R⎜ 2 − 2 ⎟
⎝3
λ
n ⎠
ovvero, in generale, del tipo
,
1
⎛ 1
1 ⎞
= R⎜ 2 − 2 ⎟
⎝4
λ
n ⎠
,
1
⎛ 1
1⎞
= R⎜ 2 − 2 ⎟
⎝1
n ⎠
λ
⎛ 1
1
1 ⎞
= R⎜
−
⎟
λ
⎝ ( n' ) 2 (n ") 2 ⎠
(2)
dove n' individua la serie (2 per Balmer) e n"=n'+1, n'+2, ecc. Nel 1908, Paschen
trovò due nuove linee dell'idrogeno nell'infrarosso, le cui lunghezze d'onda si
ottenevano con n'=3 e n"=4 e 5. In tabella sono riportate le altre serie
successivamente scoperte.
Nome della serie
Anno della scoperta
Valori di n' e n"
Lyman
Balmer
Paschen
Brackett
1906-1914
1885
1908
1922
n'=1; n"=2,3,....
n'=2; n"=3,4,....
n'=3; n"=4,5,....
n'=4; n"=5,6,....
Pfund
1924
n'=5; n"=6,7,....
Prof. V. Augelli
- COMPLEMENTI DI FISICA I -
A.A. 2005/2006
23
Vista la regolarità con cui le linee spettrali si presentavano, Ritz enunciò una
legge empirica, nota come "principio di combinazione", la quale afferma che la
frequenza di una qualunque riga spettrale è data dalla differenza di due termini,
caratteristici del corpo, del tipo R/n'2 e R/n2 .
Struttura atomica e modello di Bohr.
Quando Niels Bohr iniziò ad occuparsi della struttura atomica, il modello più
avanzato era quello di Rutherford. Ma questo mostrava due grossi punti deboli.
1) Il modello non era capace di spiegare gli spettri a righe; 2) gli elettroni
dovrebbero cadere sui nuclei a causa dell'attrazione elettrostatica se fossero
fermi a una certa distanza oppure emettendo luce con frequenza pari alla
frequenza orbitale (spettro continuo) poiché crescente è la velocità con cui
l'elettrone dovrebbe spiralizzare se fosse in moto intorno al nucleo. L'atomo
collasserebbe in un tempo dell'ordine del picosecondo. Ma Planck aveva provato
che l'atomo-oscillatore scambia energia in maniera discontinua. Bohr (1913) fece
allora le seguenti ipotesi: 1) l'elettrone si mantiene su un'orbita stabile
(stazionaria) senza irradiare energia; l'equilibrio dinamico del sistema è
governato dalle leggi della meccanica classica.
L'assunzione che la frequenza ν del quanto scambiato fosse uguale alla
frequenza di oscillazione o rotazione, f, dell'elettrone nell'atomo non era stata
provata. Il problema era che l'elettrone passando da un'orbita ad un'altra
doveva mantenere costante la frequenza orbitale. Ma, se assumiamo che la forza
agente sull'elettrone nel suo moto orbitale intorno al nucleo, sia la forza
centripeta coulombiana, si ottiene:
ma,
v = 2 πrf , per cui:
m e v 2 ke 2
= 2
r
r
(3)
⎛ 4π 2 m e ⎞ 3
1
2
=T =⎜
⎟r
2
f2
⎝ ke ⎠
(4)
cioè, vale la terza legge di Keplero e quindi la radiazione non può essere emessa
a frequenza costante (cioè, non si può osservare uno spettro a righe) nella
transizione tra orbite stabili. Il modello sembrava quindi fallire se si usavano le
leggi della meccanica classica.
Prof. V. Augelli
- COMPLEMENTI DI FISICA I -
A.A. 2005/2006
24
Allora Bohr stabilì un secondo postulato che affermava la possibilità di usare le
leggi della meccanica classica quando l'elettrone si trovava sulle orbite
stazionarie e l'impossibilità quando esso passava tra stati stazionari diversi.
2) Un elettrone dell'atomo può passare da uno stato stazionario ad un altro
assorbendo o emettendo energia sotto forma di quanti di radiazione di
frequenza ν=(E"-E')/h, indipendentemente dalla frequenza f del suo moto
orbitale e ciò significava che f e ν erano diversi.
Bohr assunse inoltre che:
3) le orbite degli elettroni sono circolari e il momento angolare è quantizzato: L
= n h , essendo n un intero positivo e h =h/2π. Ciò implica che non le infinite
orbite classiche sono possibili, ma solo quelle per cui il momento angolare è un
multiplo intero di h .
Sebbene tale modello permettesse di spiegare gli spettri a righe dell'atomo
d'idrogeno, esso non consentiva di fissare uno zero per l'energia. Bohr mise in
relazione la frequenza f e l'energia dell'elettrone nella sua orbita stabile;
questa è data dalla somma dell'energia cinetica e di quella potenziale:
2
1
Ze
(5)
E = m e v2 −
r
2
1
1 Ze2
1 Ze2
2
ma
per
cui
(cioè l'energia è negativa) e quindi
me v =
E =−
2
2 r
2 r
1 Ze2
. Sostituendo nella (4) otteniamo
r =−
2 E
2 (−E )3/ 2
(6)
f=
πZe2 m
(l’energia è negativa per cui –E è positivo).
Allora Bohr suppose che l'elettrone è praticamente fermo a distanza molto
grande dal nucleo cosicchè la sua energia e frequenza di rivoluzione sono nulle;
se l'elettrone viene catturato dall'atomo e si situa in uno stato per cui vale la
(6), esso emetterà luce di frequenza pari alla media delle frequenze che
l'elettrone aveva nello stato iniziale e in quello finale, cioè ν=f/2, inoltre, sulla
base della teoria di Planck, l'energia emessa sarà un multiplo intero di hν, cioè
nhν, essendo n il numero di quanti emessi. Sostituendo l'energia nella (6) si ha:
2 π m ee Z
ν=
h3n 3
2
e quindi
4 2
(7)
−2π2 me e 4 Z 2
E=
h 2 n2
(8)
Posto n=1, Bohr determinò l'energia di ionizzazione dell'atomo d'idrogeno e
trovò il valore calcolato essere in ottimo accordo con il valore sperimentale. Per
Prof. V. Augelli
- COMPLEMENTI DI FISICA I -
A.A. 2005/2006
25
spiegare gli spettri, Bohr cambiò il significato di n identificandolo con il numero
dell'orbita stabile da 1 a infinito, e non più con il numero di quanti emessi o
2
1 Ze
assorbiti in una transizione. Sostituendo la (8) nella espressione r = −
, si
2 E
trova
che
il
raggio
dell'orbita
h2 n2
r=
4 π2 me e 2Z
n-sima
è
proporzionale
a
n2:
(9)
Le orbite con basso n sono più vicine al nucleo e hanno maggiore energia; l'orbita
più bassa ha un raggio di 0.53 Å.
Facendo uso della condizione di quantizzazione del momento angolare si possono
ricavare facilmente quelle relative ai raggi delle orbite e all’energia. Infatti, per
mv2 Ze2
un'orbita circolare:
= 2 , ma L = mvr = nh , per cui potremo scrivere:
r
r
2
2
2 2
Ze
n h
2 h
=
da cui r n = n
. Se si assume nullo il potenziale dell'elettrone
Ze 2m
r 2n
mr 3n
2
1 Ze
all'infinito, la sua energia totale è E = −
e quindi l'energia sulla n-sima
2 r
orbita è:
1 Z 2e 4m
E =−
.
2 n 2h 2
In base al postulato di Planck, la frequenza della radiazione emessa
dall'elettrone che passa da un'orbita n" ad energia E" ad una n' con energia E',
risulta essere:
2
4 2
2
4 2
E "− E' ⎡ 2 π m e e Z ⎤ ⎡ 2π me e Z ⎤
− −
=
ν=
= ⎢−
h
h 3 (n" )2 ⎥⎦ ⎢⎣
h3 (n' )2 ⎥⎦
⎣
2 π 2 m e e 4Z 2 ⎡ 1
1 ⎤
=
⎢
3
2 −
(n")2 ⎦⎥
h
⎣ ( n' )
(10)
E in termini di lunghezza d'onda:
1 ⎤
1 2π2 m ee 4 Z 2 ⎡ 1
=
⎢
3
2 −
( n" )2 ⎦⎥
λ
ch
⎣ (n' )
2 π m ee Z
La costante
ch3
2
4
2
(11)
vale proprio R per cui si trova un ottimo accordo con i
dati sperimentali. In figura sono riportate tutte le serie compresa la Lyman
identificata nel 1914 (quindi dopo l'elaborazione del modello). Le orbite
corrispondenti ai valori di n=1, 2, 3, .....sono note come orbite K, L, M, ....
Bohr estese i suoi risultati per spiegare la serie di Pickering che era del tipo
Prof. V. Augelli
- COMPLEMENTI DI FISICA I -
A.A. 2005/2006
26
⎛
⎞
1
1
1
= R⎜
−
⎟
λ
⎝ ( n' /2 ) 2 ( n" /2 ) 2 ⎠
(12)
Egli attribuì tali linee all'elio ionizzato (He+); infatti, se si ripete il ragionamento
che ha condotto alla (11), assumendo che l'elettrone è su orbite intorno ad un
nucleo di carica 2e, si trova la (12). Bohr estese tale risultato agli atomi con Ze
protoni e ionizzati Z-1 volte, per cui nella (12), 22 è sostituito da Z2. Il modello
proposto da
Bohr spiegava oltre che gli spettri di emissione anche quelli di assorbimento sia
a righe che continui.
Gli spettri continui corrispondevano ad assorbimento a tutte le frequenze e solo
gli elettroni liberi possono assorbire qualunque ammontare di energia. Esiste
quindi una frequenza di soglia ν o = ∆E / h per cui si ha la completa
ionizzazione dell'atomo ( ∆E è l'energia necessaria per portare l'elettrone dallo
stato fondamentale a n= ∞ ).
Successivamente Bohr tenne conto che la massa del nucleo è finita anche se
molto più grande della massa dell'elettrone. In tal caso il sistema è costituito da
nucleo ed elettrone in moto intorno al centro di massa del sistema. Si trova che
1 Z 2e 4µ
mM
E =−
la massa ridotta e
2 2 , essendo µ =
2 n h
m+M
Prof. V. Augelli
- COMPLEMENTI DI FISICA I -
A.A. 2005/2006
27
1 ⎤
1 µ 2 π2 me e 4Z 2 ⎡ 1
=
⎢
3
2 −
(n")2 ⎦⎥
λ m
ch
⎣ (n' )
cioè la costante di Rydberg per un nucleo di massa M è µ / m volte quella
relativa ad un nucleo di massa infinita. Con questa correzione, l'accordo con i
dati sperimentali migliora.
L'esperimento di Franck ed Hertz.
Una verifica sperimentale dell'esistenza dei livelli energetici negli atomi fu
fornita da Franck ed Hertz nel 1914. L'apparato sperimentale è costituito da un
tubo di vetro contenente vapori di mercurio a bassa pressione. Un filamento
metallico, C, che funge da catodo, emette elettroni per effetto termoionico che
vengono accelerati verso una griglia A da una differenza di potenziale V.
Mantenendo la placca P ad un
potenziale minore di quello di G mediante un opportuno potenziale ritardante Vr,
gli elettroni giungeranno in P se lasciando A hanno energia cinetica sufficiente.
Gli elettroni raccolti da P danno luogo ad una corrente che viene misurata in
funzione del potenziale accelerante V. Come si può osservare in figura, per bassi
valori di V, la corrente aumenta con V sino a V=4.9 V e successivamente
decresce rapidamente.
Prof. V. Augelli
- COMPLEMENTI DI FISICA I -
A.A. 2005/2006
28
Quello che accade è che gli elettroni spesso urtano gli atomi di mercurio in
maniera elastica per cui la loro energia cinetica rimane praticamente la stessa
dopo l'urto.
Se, però, l'energia cinetica acquistata per effetto del potenziale accelerante è
sufficiente ad eccitare l'atomo di mercurio per cui l'elettrone dell'atomo passa
Prof. V. Augelli
- COMPLEMENTI DI FISICA I -
A.A. 2005/2006
29
dallo stato fondamentale al primo livello eccitato, l'elettrone urtante cederà la
maggior parte della sua energia (e l'urto sarà quindi anelastico) e arriverà su A
con una quantità di energia che non gli permetterà di superare l'opposizione di
Vr. La corrente pertanto diminuirà. Aumentando V, dopo il primo urto anelastico,
la corrente riprenderà ad aumentare fino a che l'energia posseduta non è tale
da portare l'elettrone atomico al secondo livello eccitato per cui l'atomo
assorbe una energia pari a E2-E0 e la corrente nuovamente diminuisce. Nel caso
del mercurio risulta quindi che la separazione tra livello fondamentale e primo
livello eccitato è di 4.9 eV; la controprova è fornita dall'osservazione di una
linea a tale frequenza (λ=2536 Å) nello spettro di emissione del mercurio; tale
linea non si osservava a tensioni minori di 4.9 V. Il modello atomico di Bohr
risultava così in eccellente accordo con i dati sperimentali.
Prof. V. Augelli
- COMPLEMENTI DI FISICA I -
A.A. 2005/2006
30