Soluzioni della prova di Matematica
Maturità 2015
Lara Charawi1 , Alberto Cogliati2 e Luca Magri2
1
2
Dipartimento di Matematica, Università degli Studi di Pavia
Dipartimento di Matematica, Università degli Studi di Milano
18 giugno 2015
Problema 1
1. La funzione che esprime la spesa totale in un mese è f (x) = 10 +
1
x; la funzione g(x) che
10
f (x)
; per entrambe le funzioni si intende che il loro
x
10
dominio sia R+ . Il grafico di g(x) è un ramo di iperbole equilatera; poiché g 0 (x) = − 2 , g è
x
una funzione strettamente monotona decrescente e pertanto non ammette né massimi né minimi.
Ciò è coerente con il suo significato di costo medio: al crescere dei minuti di conversazione si
ammortizzano i costi derivanti dal canone fisso.
esprime il costo medio al minuto è g(x) =
2. Dall’equazione
g(x1 ) =
ricaviamo
g(x0 )
2
1
5
1
200x0
10
+
=
+
⇒ x1 =
.
x1
10
x0
20
100 − x0
La funzione cosı̀ ottenuta x1 = h(x0 ) è una funzione omografica avente asintoto verticale x0 = 100
e asintoto orizzontale x1 = −200 come illustrato in Figura 1a. Osserviamo che per valori di x0
maggiori di 100, x1 è negativa e pertanto priva di significato per il problema che si sta trattando.
Concludiamo che il significato dell’asintoto verticale x0 = 100 è quello di essere il limite superiore
oltre il quale non è più possibile dimezzare il costo medio. Vale a dire che se nel mese precedente i
minuti di chiamate sono stati uguali o superiori a 100 non è possibile, nel mese presente, dimezzare
il costo medio (del mese precedente).
3. Cerchiamo una funzione del tipo P (x) = ax 2 + bx + c che passi per i punti A(0, 2), B(2, 7/2),
C(4, 4). Imponendo il passaggio per questi tre punti (le condizioni sono sufficienti a determinare
1
i coefficienti) troviamo a = − , b = 1, c = 2. Con riferimento alla Figura 1b calcoliamo l’area
8
AODHA ; essa è data dall’integrale
Z 6
P (x)dx = 21.
0
1
1
L’area non coperta dal segnale, AOT R , è data da . Troviamo la percentuale p corrispondente
2
AOT R rispetto al totale dell’area, AOKHA . Essa è
p=
100 · 1/2
≈ 2, 38%.
21
La zona coperta dal segnale risulta quindi pari a 100% − 2, 38% = 97, 62% del totale. Concludiamo
che l’informazione riportata dal sito non è veritiera.
4. Le funzioni f e g del nuovo piano tariffario sono date da:
x
10 + 10 , x < 500
f (x) =
60 + x − 500 x ≥ 500
5
e da
g(x) =
10
x
−40
x
+
1
,
10
(1)
x < 500
(2)
1
+
5
x ≥ 500.
La funzione f (x), che è continua per x > 0, è una spezzata costituita da due rette. Essa è continua
in x = 500, come si verifica immediatamente, ma ivi non derivabile. Presenta infatti un punto
angoloso. La funzione è monotona (strettamente) crescente, in coerenza con il fatto che si tratta
di un costo cumulativo.
La funzione g(x), riportata in Figura 1d, è continua per x > 0, ha x = 0 come asintoto verticale
e y = 1/5 come asintoto orizzontale per x → +∞. La funzione è monotona decrescente per
0 < x < 500 e monotona crescente per x > 500. In x = 500, g presenta un punto di non derivabilità,
più precisamente un punto angoloso. g presenta inoltre un minimo assoluto in corrispondenza di
x = 500. Osserviamo che l’andamento crescente di g per x > 500 è dovuto al fatto che da quel
momento in poi il costo medio per minuto è pari a 20 centesimi di euro (1/5 di euro), che coincide
con l’intercetta dell’asintoto orizzontale, come ci aspettavamo.
Problema 2
Dal momento che g è una primitiva di f nell’intervallo [−3, 3], vale g 0 (x) = f (x) per ogni x ∈
[−3, 3].
1. Se f (x) fosse un polinomio il suo grado minimo sarebbe 4.
Dal grafico di f si può notare che f ha tre radici in [−3, 3], di cui una per x = 2 di molteplicità
2, perché annulla anche la derivata f 0 (x), ma non la derivata seconda (non si ha un cambio di
concavità).
2. Essendo f la derivata di g lo studio del segno di f permette di determinare i massimi e minimi
relativi di g. In particolare:
in [-3,-2] f < 0 ⇒ g &
in [-2, 0] f > 0 ⇒ g %
2
(a)
(b)
(c)
(d)
Figura 1
in [0, 3] f < 0 ⇒ g &.
Quindi g(x) ha un massimo relativo in x = 0. Analogamente, lo studio della monotonia di f (quindi
del segno di f 00 ci permette di determinare la concavità in [-3,-1] f % ⇒ g 00 > 0
in [-1, 1] f & ⇒ g 00 < 0
in [1, 2] f % ⇒ g 00 > 0.
in [2, 3] f & ⇒ g 00 < 0.
g è concava verso l’alto dove la g 00 è positiva ovvero in [-3,-1] e [2,3].
3. Utilizzando il teorema fondamentale del calcolo integrale
Z 3
f (t)dt = g(3) − g(0).
0
Sapendo che g(3) = −5 e
Z
3
f (t)dt = −3 − 1 = −4
0
3
si ottiene
g(0) = −5 + 4 = −1.
0
1 + g(x)
una forma indeterminata del tipo , per calcolare il limite si può utilizzare il
Essendo
2x
0
teorema di De l’Hôpital
1 + g(x)
f (0)
lim
=
= 0.
x→0
2x
2
4. Definiamo la variabile t := 2x + 1,
Z 1
Z
h(x)dx =
−2
1
Z
−2
=
3
2
3
3f (2x + 1)dx =
Z
−3
3
f (t)dt
2
3
9
3
f (t)dt = (−2 − 3 + 3 − 1) = −
2
2
−3
Questionario
1. La funzione f è una primitiva di f 0 (x) = −2x 2 + 6. Pertanto essa è da ricercarsi fra tutte le
funzione del tipo fc (x) = − 23 x 3 + 6x + c, dove c indica una costante arbitraria. Poiché la retta data
è tangente al grafico della curva richiesta, cerchiamo per quali valori della variabile x la derivata di
fc (x) è uguale a −2. Otteniamo i valori x = ±2. Poichè la retta è tangente al grafico di f nel
secondo quadrante, il valore x = 2 è da escludere. Il grafico di fc (x) deve passare per il punto
(−2, 9). Otteniamo cosı̀ il valore c = 47
3 .
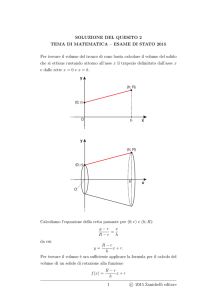
2. Per calcolare il volume del tronco di cono T , consideriamo come in Figura 2 il cono C che
si ottiene prolungando la superficie laterale di T . Il volume VT del tronco di cono T è dato dalla
differenza tra il volume del cono C e quello del cono C 0 avente per base la faccia superiore del tronco
di cono e come altezza h0 la differenza tra l’altezza di C e quella di T : VT = VC − VC 0
Ricordandosi che il volume di un cono è pari a un terzo del volume di un cilindro con la stessa base
e la stessa altezza, si ricava
VC =
πR2 (h + h0 )
πr 2 (h0 )
, VC 0 =
.
3
3
Possiamo osservare che i triangoli DAL e LBI sono simili, ossia
h0 : r = h : (R − r )
e quindi
h0 =
hr
.
R−r
4
A questo punto esprimiamo h0 in funzione dell’altezza del tronco di cono e otteniamo:
πR2 (h + h0 ) πr 2 h0
−
3
3
πR2 h
πR2 (hr )
πr 2 (hr )
=
+
−
3
3(R − r ) 3(R − r )
πh
r2
R2 r
2
=
R +
−
3
R−r
R−r
3
πh R − r 2
=
3
R−r
πh (R − r )(R2 + r 2 + Rr )
,
=
3
R−r
VT = VC − VC 0 =
semplificando otteniamo quindi
VT =
πh
R2 + r 2 + Rr .
3
Figura 2
3. Il numero di modi (o combinazioni) in cui si può ottenere k volte testa su 6 lanci è k6 ognuno con
6
1
1
probabilità
=
, perché supponiamo che la moneta non sia truccata e quindi la probabilità
2
64
di ottenere testa con un lancio è pari a 12 . Quindi, la probabilità di ottenere esattamente k volte
testa in 6 lanci di moneta sarà
6
6
1
P (k) =
.
k
2
5
La probabilità che esca testa al più 2 volte sarà data dalla somma della probabilità che esca 2, 1 e
0 volte, cioè
P (k ≤ 2) = P (k = 0) + P (k = 1) + P (k = 2)
=
2 X
6
1
=
k
64
k=0
=
1
1
22
1
+6
+ 15
=
.
64
64
64
64
La probabilità che esca almeno 2 volte testa invece
P (k ≥ 2) = P (k = 2) + P (k = 3) + P (k = 4) + P (k = 5) + P (k = 6) = 1 − P (k = 0) − P (k = 1),
dove abbiamo sfruttato il fatto che la somma delle probabilità degli eventi realizzabili è 1, cioè
P (k = 0) + P (k = 1) + P (k = 2) + P (k = 3) + P (k = 4) + P (k = 5) + P (k = 6)
P (k ≥ 2)
6
1
6
1
= 1 − P (k < 2) = 1 − P (k = 0) + P (k = 1) = 1 −
−
=
64
64
0
1
1
7
57
1
−6
=1−
=
.
= 1−
64
64
64
64
4. Calcoliamo la derivata prima e la derivata seconda della funzione y =
y0 =
1 − ln x
,
x2
y 00 =
ln(x)
. Otteniamo:
x
2 ln x − 3
.
x3
Si verifica facilmente che y = y (x) è soluzione della quarta equazione differenziale.
5. La retta passante per l’origine O ortogonale al piano dato è descritto dai punti P = O + tv dove
v è il vettore che rappresenta la normale al piano, come illustrato in Figura 3. Dal momento che le
componenti di v sono descritte dai coefficienti dell’equazione cartesiana del piano abbiamo
1
v = 1
−1
e di conseguenza un generico punto della retta cercata sarà della forma
0
1
t
x
P = y = 0 + t 1 = t .
−t
z
0
−1
Possiamo descrivere la retta in forma cartesiana come intersezione di due piani: basta porre t = −z,
quindi da x = t e y = t si ha
x +z =0
y +z =0
6
Figura 3
6. Calcoliamo la derivata prima della funzione assegnata. Essa è data da:
f 0 (x) = 2 [(x − 1) + (x − 2) + (x − 3) + (x − 4) + (x − 5)] = 10(x − 3).
(3)
Lo studio del segno della funzione derivata ci restituisce il minimo x = 3.
7. L’area del triangolo AOB disegnato in Figura 4 si può calcolare tramite una nota regola della
trigonometria
1
2π
A(AOB) = r 2 si n ,
2
n
dunque l’area del poligono è
1
2π
A(n) = nA(AOB) = n r 2 si n .
2
n
2π
1 2π
1
= lim n r 2
= r 2π
lim n r 2 si n
n→∞ 2
n→∞ 2
n
n
Figura 4
7
(4)
8. L’insieme dei punti del triangolo che distano dai vertici più di 2 è indicato dall’ombreggiatura in
Figura 5. Indichiamo con T la sua area. La probabilità richiesta è data dal rapporto tra T e l’area
totale del triangolo che indichiamo con A. Calcoliamo T trovando la somma S delle aree dei 3
settori circolari indicati in figura. Indicando con α, β, γ gli angoli del triangolo, è facile convincersi
che
r2
S = (α + β + γ),
2
dove con r si intende il raggio dei tre settori circolari che è pari a 2. Poiché α + β + γ = π,
otteniamo S = 2π. La probabilità è dunque
A−S
T
= .
A
A
Non resta che trovare l’area del√triangolo. Applicando√il teorema di Pitagora calcoliamo l’altezza h
5 119
119
. Dunque A =
. Ricaviamo infine:
relativa al lato minore; essa è
2
4
p ≈ 54%.
p=
Figura 5
9. Consideriamo la funzione assegnata:
f (x) =
x3 0 ≤ x ≤ 1
x − kx + k 1 < x ≤ 2.
2
(5)
Affinché le ipotesi del teorema di Lagrange siano soddisfatte è necessario che la funzione sia continua
sull’intervallo chiuso [0, 2] e derivabile sull’intervallo aperto (0, 2). Osserviamo che la funzione f è
continua in x = 1 per ogni valore di k. Occorre pertanto imporre la derivabilità della funzione in
x = 1. Dall’uguaglianza della derivata sinistra e destra
lim
h→0−
f (1 + h) − f (1)
f (1 + h) − f (1)
= lim+
h
h
h→0
(6)
otteniamo, con facili calcoli, k = −1. Per trovare il punto c ∈ [0, 2] soddisfacente alla tesi del
teorema di Lagrange, è sufficiente risolvere l’equazione
f 0 (c) =
f (2) − f (0)
.
2
8
p
L’unica soluzione accettabile è data da c = + 5/6.
√
10. Sia E l’intersezione del grafico della curva x 7→ x con la retta x = 1 come mostrato in
√
Figura 6. Osserviamo che il punto di intersezione del grafico di x con la retta x = 4 coincide col
vertice C. Pertanto, l’area AABCE è data dall’integrale
Z 4
√
14
2 h√ 3 i4
=
xdx =
x
.
3
3
1
1
4
14
= . Il rapporto richiesto
Per differenza con l’area del rettangolo (uguale a 6), AECD = 6 −
3
3
è
AECD
2
r=
= .
AABCE
7
Figura 6
9