Insiemi della retta reale
1
Insiemi limitati e illimitati
Definizione 1.1 Un insieme X ⊂ R si dice limitato inferiormente se esiste
L ∈ R tale che per ogni x ∈ X si abbia L ≤ x; X si dicelimitato superiormente se esiste L ∈ R tale che per ogni x ∈ X si abbia x ≤ L; X si dice
limitato se è limitato sia inferiormente che superiormente.
Gli esempi principali sono gli intervalli: siano a, b ∈ R con a < b, allora
definiamo i seguenti insiemi
(a, b) = {x ∈ R | a < x < b}
[a, b) = {x ∈ R | a ≤ x < b}
(a, b] = {x ∈ R | a < x ≤ b}
[a, b] = {x ∈ R | a ≤ x ≤ b}
(−∞, b) = {x ∈ R | x < b}
(−∞, b] = {x ∈ R | x ≤ b}
(a, ∞) = {x ∈ R | a < x}
[a, ∞) = {x ∈ R | a ≤ x}
(intervallo aperto)
(intervallo aperto a sinistra)
(intervallo aperto a destra)
(intervallo chiuso)
(semiretta aperta a destra)
(semiretta chiusa a destra)
(semiretta aperta a sinistra)
(semiretta chiusa a sinistra)
Con (−∞, ∞) si intende tutta la retta reale R.
Definizione 1.2 Se X è un insieme limitato inferiormente, il suo estremo
inferiore inf X è l’unico numero reale e tale che per ogni x ∈ X si abbia e ≤ x
e per ogni > 0 esista x ∈ X tale che x < e + .
In altri termini l’estremo inferiore è il più grande dei numeri che sono minori
o uguali ad ogni altro numero dell’insieme.
Definizione 1.3 Se X è un insieme limitato superiormente, il suo estremo
superiore sup X è l’unico numero reale e tale che per ogni x ∈ X si abbia
x ≤ e e per ogni > 0 esista x ∈ X tale che e − < x .
1
2 PUNTI ED INSIEMI DI R
2
In altri termini l’estremo inferiore è il più piccolo dei numeri che sono maggiori
o uguali ad ogni altro numero dell’insieme.
Ad esempio a è l’estremo inferiore degli intervalli (a, b), [a, b), (a, ∞),...,
e b è l’estremo superiore degli intervalli (a, b), (a, b], (−∞, b),...
Definizione 1.4 Se inf X ∈ X allora inf X si dice minimo di X, mentre se
sup X ∈ X allora sup X si dice massimo di X.
2
Punti ed insiemi di R
Definizione 2.1 Un punto interno di un insieme X ⊂ R è un punto x ∈ X
tale che esista un intervallo aperto A che contenga x e tutto contenuto in X,
cioè tale che esista un > 0 tale che per ogni x0 tale che |x − x0 | < si abbia
x0 ∈ X.
Ad esempio il punto 1 è interno all’insieme (0, 2), ma non all’insieme (0, 1);
non è nemmeno interno all’insieme (0, 1], pur appartenendogli.
Definizione 2.2 Un punto esterno di un insieme X ⊂ R è un punto x che
è interno a R \ X.
Ad esempio il punto 0 è esterno all’insieme (1, 2), ma non all’insieme (0, 1).
Non si confondano i punti esterni con quelli non appartenenti a X: ad esempio
0 non appartiene a (0, 1) ma non è un suo punto esterno. È vero invece che
se x è esterno a X allora x ∈
/ X.
Definizione 2.3 Un punto di aderenza o punto di frontiera di un insieme
X ⊂ R è un punto x ∈ R che non è né interno né esterno ad X.
Ad esempio il punto 0 è di aderenza per l’insieme [0, 1), ma non per (−1, 1)
al quale è interno.
Definizione 2.4 Un punto di accumulazione di un insieme X ⊂ R è un
punto x ∈ R tale che per ogni intervallo di centro x contiene un punto x0 ∈ X
diverso da x, cioè tale che per ogni > 0 esista x0 ∈ X tale che |x − x0 | < .
Ad esempio 0 è un punto di accumulazione per X = (−1, 0) ∪ (0, 1).
3 INSIEMI APERTI E CHIUSI
3
NB: un punto di aderenza non è necessariamente un punto di accumulazione:
ad esempio l’insieme X = {1} ∪ (2, 3) ha 1,2 e 3 come punti di aderenza,
mentre i suoi punti di accumulazione formano l’intervallo [2, 3].
Definizione 2.5 Un punto isolato di un insieme X ⊂ R è un punto x ∈ X
che non è di accumulazione, cioè tale che esista almeno un tale che per
ogni x0 tale che |x − x0 | < sicuramente si ha x0 ∈
/ X.
Ad esempio il punto 1 dell’insieme X = {1} ∪ (2, 3) è isolato.
Si noti che
{punti interni} ∩ {punti esterni} = ∅
{punti interni} ∩ {punti di aderenza} = ∅
{punti esterni} ∩ {punti di aderenza} = ∅
{punti isolati} ∩ {punti di accumulazione} = ∅
{punti isolati} ⊂ {punti di aderenza}
{punti interni} ⊂ {punti di accumulazione}
3
Insiemi aperti e chiusi
Definizione 3.1 Un insieme X ⊂ R è aperto se ogni suo punto è interno,
cioè se per ogni x ∈ X esiste > 0 tale che per ogni x0 tale che |x − x0 | < si abbia x0 ∈ X.
In parole povere un insieme X è aperto se per ogni x ∈ X esiste un intervallo
aperto (x − , x + ) tutto contenuto in X.
Definizione 3.2 Un insieme X ⊂ R è chiuso se complementare di X, R\X,
è un insieme aperto
Teorema 3.1 Dire che un insieme X è chiuso equivale a dire che X contiene
tutti i suoi punti di accumulazione.
Teorema 3.2 Dire che un insieme X è chiuso equivale a dire che X contiene
tutti i suoi punti di aderenza.
Definizione 3.3 Se X ∈ R è un qualsiasi insieme allora il più piccolo insieme che contiene X e che è chiuso si dice chiusura di X e si denota con
X̄.
3 INSIEMI APERTI E CHIUSI
4
Ad esempio la chiusura di [0, 1) è [0, 1]; ovviamente X coincide con la sua
chiusura se e solo se è vuoto.
Teorema 3.3 Se A0 , A1 , A2 , ... sono insiemi aperti allora la loro unione
[
An = A0 ∪ A1 ∪ · · ·
n∈N
è ancora un aperto; in particolare se da un certo n in poi An = ∅ troviamo
che l’unione di un numero finito di aperti è un aperto.
Teorema 3.4 Se A0 , A1 , ..., An sono aperti allora anche la loro intersezione
n
\
Ai = A0 ∩ A1 ∩ · · · ∩ An
i=0
è un aperto.
NB: l’intersezione di una successione non finita di aperti non è in generale un
insieme aperto: ad esempio consideriamo gli aperti An = (−1/(n + 1), 1/(n +
1)), cioè
A0 = (−1, 1),
A1 = (−1/2, 1/2),
A2 = (−1/3, 1/3), ...
Allora l’intersezione di tutti questi insiemi è il singolo punto 0 che è un
insieme chiuso.
Poiché passando al complementare il ruolo di unione e intersezione “si
scambiano”, troviamo i risultati seguenti per gli insiemi chiusi:
Teorema 3.5 Se C0 , C1 , C2 , ... sono insiemi chiusi allora la loro intersezione
\
Cn = C0 ∩ C1 ∩ · · ·
n∈N
è ancora un chiuso; in particolare se da un certo n in poi Cn = ∅ troviamo
che l’intersezione di un numero finito di chiusi è un chiuso.
Teorema 3.6 Se C0 , C1 , ..., Cn sono chiusi allora anche la loro unione
n
[
i=0
è un chiuso.
Ci = C0 ∪ C1 ∪ · · · ∪ Cn
4 ESERCIZI
5
NB: l’unione di una successione non finita di chiusi non è in generale un
insieme chiuso: ad esempio consideriamo i chiusi An = [1/(n + 1), ∞), cioè
A0 = [1, ∞),
A1 = [1/2, ∞),
A2 = [1/3, ∞), ...
Allora l’unione di tutti questi insiemi è (0, ∞) che è un insieme aperto.
Gli insiemi chiusi sono collegati ai limiti:
Teorema 3.7 Dire che un insieme X è chiuso equivale a dire che per ogni
successione (xn ) di elementi di X se esiste il limite x = limn→∞ xn allora x
deve appartenere a X.
Come è noto, una successione convergente è limitata: il viceversa non è vero;
ad esempio la successione xn = (−1)n (2 + 1/(n + 1)) è limitata, dato che
|xn | ≤ 3
ma non possiede limite; tuttavia la sottosuccessione ottenuta prendendo gli
indici pari x2n converge a 2. Questo fatto è vero in generale.
Teorema 3.8 Se (xn ) è una successione limitata allora se ne può estrarre
una sottosuccessione convergente.
In generale non è vero che se X è chiuso allora da una successione di elementi di X se ne possa estrarre una convergente: ad esempio se X = [0, ∞)
allora la successione (n) non possiede nessuna sottosuccessione convergente;
se tuttavia X è limitato questo è possibile.
Definizione 3.4 Un insieme è compatto se è chiuso e limitato.
Allora abbiamo il teorema di Bolzano–Weierstrass:
Teorema 3.9 Dire che un insieme X è compatto equivale a dire che se (xn )
è una qualsiasi successione di elementi di X allora se ne può estrarre una
sottosuccessione convergente.
4
Esercizi
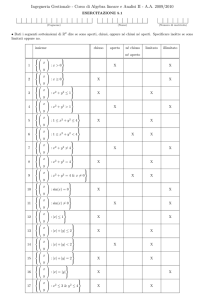
Dire se i seguenti insiemi sono limitati oppure no, e calcolarne eventuali
estremo superiore, estremo inferiore, massimi e minimi.
4 ESERCIZI
6
1)
1
|n ∈ N
n+3
2)
n2 | n ∈ Z
n3 | n ∈ Z
3)
4)
(−1)n −
1
|n ∈ N
n+1
5)
3n − 2
|n ∈ N
2n + 1
6)
n2 + 5n + 3 | n ∈ N
7)
x ∈ R | x2 ∈ Q
8)
1
N∪ −
|n ∈ N
n+1
9)
10)
t+1
| t ∈ R, t > 2
t−2
n
o
nπ
sen
|n ∈ Z
8
11)
|x| | x2 + x < 2
Per i seguenti insiemi X trovare: punti di accumulazione A, punti isolati I e
punti di aderenza F , e dire se sono chiusi o aperti nel caso in cui lo siano.
12) X = (−∞, 2 ∪ {3} ∪ (4, ∞)
13) X = {n2 | n ∈ Z}
14) X = {(−1)n | n ∈ Z}
15) X = {x2 | x ∈ R} ∩ Q
16) X = {2 − arcsen (−x2 ) | |x| ≤ 1}
[le risposte sono sulla pagina seguente]
5 RISPOSTE
5
Risposte
1) max=1/3; inf = 0.
2) max=0; sup=+∞.
3) non limitato.
4) min=-3/2; sup=1.
5) min=2; sup=3/2.
6) min=3; sup=+∞.
7) inf=−∞; sup=+∞.
8) min=-1; sup=+∞.
9) inf=1; sup=+∞.
10) min=-1; max=1.
11) min=0; sup=2.
12) A = (−∞, 2] ∪ [4, ∞), I = {3}, F = {2, 3, 4}
13) A = ∅, I = X, F = X, X è chiuso.
14) A =, I = X, F = X, X è chiuso.
15) A = R+ ∪ {0}, I = ∅, F = X̄ = [0, ∞).
16) A = X̄ = [2, 2 + π/2], I = ∅, F = {2, 2 + π/2}.
7