Solo quello che ti interessa | Il teorema nella storia - Esempi d'uso
Copyright admin [email protected]
http://www.belloma.it/il-teorema-della-storia-esempi-duso/
Il teorema nella storia - Esempi d'uso
Applicazioni matematiche
- Il teorema è basilare per il calcolo delle lunghezze, aree, volume delle figure.
Alcuni esempi:
- In un quadrato di lato x, la diagonale è pari a x*RADQ(2).
- In un rettangolo di lati x e y, la diagonale è pari a RADQ(x2+y2)
- In un parallelepipedo con spigoli x,y e z, la diagonale e pari a RADQ(x2+y2
+ z2)
- In un cono di altezza h e raggio alla base r, la generatrice è pari a RADQ(h
2+y2)
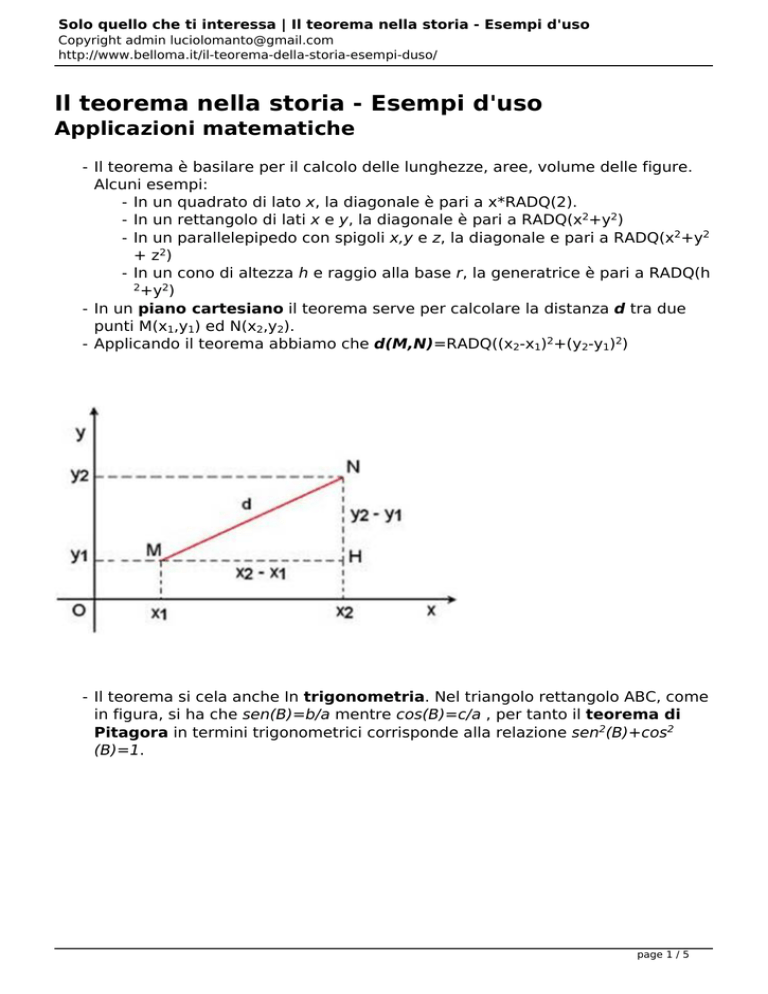
- In un piano cartesiano il teorema serve per calcolare la distanza d tra due
punti M(x1,y1) ed N(x2,y2).
- Applicando il teorema abbiamo che d(M,N)=RADQ((x2-x1)2+(y2-y1)2)
- Il teorema si cela anche In trigonometria. Nel triangolo rettangolo ABC, come
in figura, si ha che sen(B)=b/a mentre cos(B)=c/a , per tanto il teorema di
Pitagora in termini trigonometrici corrisponde alla relazione sen2(B)+cos2
(B)=1.
page 1 / 5
Solo quello che ti interessa | Il teorema nella storia - Esempi d'uso
Copyright admin [email protected]
http://www.belloma.it/il-teorema-della-storia-esempi-duso/
- Il teorema è determinante per i calcoli di topografia, le misurazione di terreni,
l’elaborazione di carte geografiche, nei problemi di navigazione marittima o
aerea, in architettura, in ingegneria e in tutti i tipi di professioni legate alle
misure.
- Prendiamo in considerazione al seguente figura:
- Qui abbiamo le relazioni tra il cerchio e il triangolo rettangolo che ha per cateti
il seno ed il coseno. Da qui si ricava la tangente (seno/coseno), la secante
(1/coseno), la cosecante (1/seno) e la cotangente (1/tangente).
page 2 / 5
Solo quello che ti interessa | Il teorema nella storia - Esempi d'uso
Copyright admin [email protected]
http://www.belloma.it/il-teorema-della-storia-esempi-duso/
- Grazie al teorema di Pitagora e alla presenza di diversi triangoli rettangoli,
possiamo ottenere in modo immediato una lunga serie di rapporti interessanti
fra queste funzioni trigonometriche, tra cui:
- L’interesse per la trigonometria scaturisce dalla geometria, dal bisogno di
misurare. La sua applicazione è in misure di architettura, agrimensura e
astronomia. Il matematico statunitense Elisha Scott Loomis disse in
proposito: “La trigonometria esiste perché esiste il Teorema di Pitagora".
- Le origini della trigonometria risalgono alla Babilonia e Egitto. Nata sia per fare
calcoli derivati da osservazioni astronomiche, sia per risolvere problemi pratici.
Procedendo alla divisione della circonferenza in 360°, il greco Ipparco (II sec.
a.C.), e più tardi Claudio Tolomeo e Menelao di Alessandria, eseguirono
laboriosi calcoli delle lunghezze delle corde in un cerchio, corrispondenti agli
angoli centrali principali.
- Indiani e arabi svilupparono tavole trigonometriche proprie da usare per calcoli
astronomici.
- I valori delle tavole trigonometriche si sono perfezionati nel tempo. Sul loro
sviluppo influirono personaggi come Fibonacci (1170-1250), Regiomontano
(1436-1476), François Viète (1540-1603), Nicolò Copernico (1473-1543) e
molti altri.
- Al discepolo di Copernico, Georg Joachim Rheticus, viene attribuita la
definizione esplicita delle funzioni trigonometriche, non più in relazione alle
corde, ma ai rapporti tra i lati di un triangolo rettangolo. Un po’ più tardi, con lo
sviluppo della geometria cartesiana, si sviluppò la trigonometria analitica
, dove furono studiate le funzioni sen(x), cos(x), tan(x)…
- Tornando al Teorema, si può affermare che questo è alla base di ogni
misurazione in quanto qualunque superficie può essere divisa in triangoli ed
ogni triangolo può essere diviso in due triangoli rettangoli. Questo consente di
stabilire altezze o distanze, altrimenti inaccessibili, a partire dalle misure di
alcuni lati ed angoli. Grazie alla conoscenza di queste relazioni, gli agrimensori
egiziani effettuavano così calcoli che ai più apparivano “divini”. Ed è per
questo che venivano venerati e considerati sacerdoti.
Distanza dall’orizzonte
page 3 / 5
Solo quello che ti interessa | Il teorema nella storia - Esempi d'uso
Copyright admin [email protected]
http://www.belloma.it/il-teorema-della-storia-esempi-duso/
- Fino a che distanza può spingersi lo sguardo, da una montagna ?
- Supponiamo di essere ad un’altezza h=1000 m dal mare e osserviamo la
seguente figura
- Dal Teorema di Pitagora possiamo scrivere d2 = (R+h)2-R2
- Sviluppando, d2 = h(h+2R), ma poiché 2R è molto maggiore di h, possiamo
approssimare 2R+h a 2R per cui d=RADQ(2Rh), sostituendo ad R il raggio della
terra pari a 6371 km e all’altezza h, pari ad 1 km, l’orizzonte O sarà a
d=RADQ(12.742)=112,88 Km
Pitagorismo di strada
- Nelle città molto spesso ci si riferisce alle distanze tra un punto e l’altro come
se si attraversassero i palazzi (in linea d’aria) e non all’effettivo tragitto da
percorrere.
- Questa situazione, che può sembrare di poco conto, può avere anche
implicazioni legali. Nel 2002 un cittadino americano fu arrestato all’angolo tra
due strade, con l’aggravante di spacciare droga a meno di 1000 piedi da una
scuola. La polizia usò il teorema di Pitagora per stabilire la distanza, che
risultava così effettivamente <1000 (in linea d’aria). Ma nella realtà la distanza
da percorrere era maggiore > 1000. Il giudice però diede ragione comunque
alla polizia.
page 4 / 5
Solo quello che ti interessa | Il teorema nella storia - Esempi d'uso
Copyright admin [email protected]
http://www.belloma.it/il-teorema-della-storia-esempi-duso/
page 5 / 5