CORSO DI POLITICA ECONOMICA
AA 2014-2015
IL MODELLO SOLOW: FONDAMENTI
DOCENTE
PIERLUIGI MONTALBANO
[email protected]
Dall’analisi di breve a quella di lungo periodo
• La crescita di LP:
Incremento tendenziale del
prodotto naturale nel corso
del tempo
• I dati mostrano che nel corso
del tempo la quantità dei
beni prodotti e gli standard
di vita aumentano
• Il PIL pro capite negli USA è oggi dieci volte superiore a quello
di un secolo fa
• Sia i tassi di crescita sia i livelli di reddito pc differiscono
enormemente tra paesi
2
Società che crescono allo 0.1-0.2% l’anno (e.g., XVIII sec.) raddoppiano la loro dimensione in una
generazione (30 anni)
Società che crescono all’1% l’anno (e.g., XIX-XX sec.) vanno incontro a cambiamenti permanenti
e profondi nell’arco di una generazione
Questioni da affrontare….
• Quali sono le determinanti della crescita?
• Quale effetto ha la crescita della popolazione sul
tasso di crescita?
• Quali effetti ha un aumento del tasso di risparmio
sulla crescita?
• Il sistema tende verso un equilibrio di lungo
periodo?
Il modello Solow (1956)
• Funzione di produzione omogenea di primo grado (offerta): Y =
F(K,L)
• Tutto espresso in termini pro-capite (o meglio per lavoratore) y =
f(k)
• Prodotto marginale del capitale decrescente (contributo alla
produzione di 1 unità aggiuntiva di capitale): f’>0 f”<0
• Funzione di investimento (spesa per nuovi impianti): i = sf(k)
• Ammortamento (% costante δk) investimenti annuali necessari a
sostituire il capitale logorato
• Variazione stock di capitale: ∆k = sf(k) – δ k (Equazione di moto)
• Stato stazionario (equilibrio di lungo periodo): per k = k*; ∆k = 0
• Il sistema tende v/stato stazionario (Equilibrio dinamico).
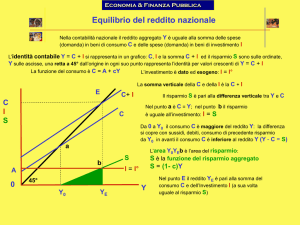
4.1. La funzione di produzione aggregata
La funzione di produzione aggregata specifica la relazione tra
produzione aggregata e input produttivi:
Y = F ( K, N )
Dove
Y= la produzione aggregata;
K= capitale : somma di macchinari, impianti, uffici e immobili;
N= lavoro: numero di lavoratori impiegati;
F= stato della tecnologia: l’insieme dei progetti che definiscono sia
la gamma di beni che possono essere prodotti nell’economia sia le
tecniche disponibili per produrli.
6
4.2. Rendimenti di scala e rendimenti dei fattori
Proprietà dei rendimenti di scala costanti: raddoppiando la scala di
produzione, cioè raddoppiando le quantità di capitale e di lavoro
impiegate, anche il prodotto raddoppia:
2Y = F (2 K ,2 N )
In generale, per ogni x:
xY = F ( xK , xN )
7
4.2. Rendimenti di scala e rendimenti dei fattori
Rendimenti decrescenti del capitale:
aumenti di capitale generano, dato il lavoro, aumenti di prodotto
tanto minori quando è maggiore il livello di capitale.
Rendimenti decrescenti del lavoro:
aumenti della quantità di lavoro, dato il capitale, generano incrementi
di prodotto tanto minori quanto maggiore è la quantità di lavoro già
impiegata.
8
4.3. Prodotto e capitale per occupato
Poniamo x uguale a 1/N e otteniamo:
Y
K
K N
= F , = F ,1
N N
N
N
Dove Y/N rappresenta il prodotto per occupato e K/N il capitale per
occupato.
L’equazione dice che la quantità di prodotto per occupato dipende
dalla quantità di capitale per occupato.
9
4.2. Rendimenti di scala e rendimenti dei fattori
Prodotto e capitale per addetto.
Aumenti del capitale per addetto provocano
incrementi sempre più piccoli del prodotto per
addetto.
Per la proprietà dei rendimenti
marginali decrescenti: nel punto A,
dove il capitale è più basso, un
aumento del capitale per occupato,
pari alla distanza AB provoca un
aumento del prodotto per occupato
pari a A’B’. Questo aumento è
maggiore di quello provocato nel
punto C, dove il capitale è più elevato,
infatti C’D’<A’B’.
10
Funzione di produzione flessibile
R.Capolupo-Appunti macro2 (grafici
e tabelle dal DeLong)
11
4.4. Le fonti della crescita
• Gli aumenti del prodotto per occupato (Y/N) possono derivare da:
– da aumenti del capitale per occupato (K/N) (nb: i sono funzione
del s)
– da miglioramenti dello stato della tecnologia che spostano la
funzione di produzione F e permettono di ottenere una maggiore
quantità di prodotto per occupato con lo stesso capitale per
occupato.
NB.
L’accumulazione di K/N (e.g. maggior tasso di S) non può sostenere
in modo permanente il tasso di crescita della produzione
L’unico processo permanente riguarda il miglioramento dello stato
della tecnologia (i.e., progresso tecnologico) – vedi oltre 12
Tasso di risparmio e produzione
13
Gli effetti di diversi tassi di risparmio.
Un paese con un maggior tasso di risparmio
raggiunge un maggior livello di produzione
per addetto in stato stazionario.
Qual è l’impatto del risparmio sulla crescita di LP?
• Due economie caratterizzate da eguale crescita ma differenti
propensioni al risparmio avranno livelli di prodotto stabilmente
differenti (maggiore per l’economia caratterizzata dal più elevato
tasso di risparmio)
• Tuttavia, entrambe le economie tenderanno allo stato stazionario
(i.e., crescita zero)
14
Miglioramento della tecnologia e produzione
15
Gli effetti di un miglioramento dello
stato della tecnologia.
Un miglioramento della tecnologia sposta in
alto la funzione di produzione, provocando
un aumento del prodotto per addetto, dato il
capitale per addetto.
Il circuito capitale, produzione, risparmio/investimento
• l’ammontare di capitale nell’economia determina il livello di
produzione
• il livello di produzione determina a sua volta il livello di
risparmio e di investimento e quindi il capitale accumulato
nel tempo
16
Canale 1: Gli effetti del capitale sulla produzione
Partendo dall’ipotesi dei rendimenti di scala, avremo:
Y
K
= F , 1
N
N
Assumiamo temporaneamente le seguenti ipotesi:
- la dimensione della popolazione, il tasso di partecipazione e il
tasso naturale di disoccupazione sono costanti;
- non esiste progresso tecnologico.
La relazione tra produzione e capitale per addetto, dal lato della
produzione, è data da:
Yt
Kt
= f
N
N
17
Canale 2: Gli effetti della produzione sull’accumulazione di
capitale
Produzione e investimento.
3 ulteriori ipotesi:
1. assumiamo un’economia chiusa
I = S + (T − G )
2. assumiamo che il risparmio pubblico (T-G) sia uguale a zero
3. assumiamo che il risparmio privato sia proporzionale al
reddito, cioè:
I = S
Otteniamo:
18
S = sY
I t = sYt
Gli effetti complessivi sull’accumulazione di capitale
Investimento e accumulazione di capitale.
L’andamento dello stock di capitale è dato da (ove l’I è un flusso):
Kt +1 = (1 − δ ) Kt + I t
Sostituendo all’I la sua relazione con il reddito e dividendo per N si
ottiene la relazione tra produzione e accumulazione di capitale:
Kt +1
Kt
Yt
= (1 − δ )
+s
N
N
N
il capitale per addetto all’anno t+1 è uguale al capitale per addetto
all’inizio dell’anno t, tenuto conto del deprezzamento, più
l’investimento per addetto effettuato nell’anno t, che a sua volta è
uguale al tasso di risparmio moltiplicato per il prodotto per addetto
nell’anno
t.
19
La dinamica del capitale e della produzione
Riordinando i termini (spostando Kt/N sul lato sinistro e
ricordando che sY = sf(K/L)) si ha
K t +1 K t
−
N
N
Variazione del
capitale dall’anno t
all’anno t + 1
=
Kt
sf
N
=
Investimento
nell’anno t
_
_
Kt
δ
N
Deprezzamento
nell’anno t
Se l’investimento per addetto eccede il deprezzamento per addetto, la
variazione del capitale per addetto è positiva: il capitale per addetto
aumenta.
Se l’investimento per addetto è inferiore al deprezzamento per
addetto, la variazione del capitale per addetto è negativa: il capitale
per addetto diminuisce.
20
La dinamica del capitale e della produzione
21
Dinamica della produzione e del capitale.
Quando il capitale e la produzione sono bassi,
l’investimento eccede il deprezzamento e il
capitale aumenta. Quando il capitale e la
produzione sono elevati, l’investimento è
inferiore al deprezzamento e il capitale
diminuisce.
Capitale e produzione in stato stazionario
La situazione in cui prodotto per addetto e capitale per addetto
sono costanti è chiamata lo stato stazionario dell’economia.
Il valore del capitale per addetto di stato stazionario è dato da:
K*
K *
sf
=δ
N
N
Dato il capitale per addetto (K*/N), il valore di stato stazionario
del prodotto per addetto (Y*/N) è dato da:
Y*
K *
= f
N
N
22
In che modo il tasso di risparmio influenza la crescita?
1. Il tasso di risparmio non ha alcun effetto sul tasso di crescita di
lungo periodo del prodotto per addetto (l’economia tende sempre
allo stato stazionario).
2. Tuttavia il tasso di risparmio determina il livello di prodotto per
addetto nel lungo periodo.
23
Tasso di risparmio e produzione
Fig. 11. 5. Gli effetti di un aumento del tasso
di risparmio sul prodotto per addetto.
Un aumento del tasso di risparmio comporta un
periodo di crescita più elevata, finché la
produzione non raggiunge il suo nuovo livello di
stato stazionario.
24
Tasso di risparmio e consumo
Il governo può utilizzare vari strumenti per influenzare il tasso di
risparmio (es. far variare il S pubblico – avanzo di bilancio – o
incentivare il S privato)
Ma esiste un tasso di risparmio ottimale?
Per analizzare questo tema è necessario spostare l’attenzione dal
risparmio al consumo (poiché le persone risparmiano
guardando al consumo e non alla produzione)
Dal punto di vista del consumo, il risparmio riduce il consumo
attuale e (come vedremo) non necessariamente ne provoca un
aumento nel lungo periodo (ad occupazione costante).
25
Due casi estremi
• Un’economia con tasso di risparmio uguale a zero ha
accumulazione di capitale uguale a zero e quindi consumo
nullo nel lungo periodo.
• Un’economia con tasso di risparmio uguale a 1, avrà livelli di
capitale e produzione elevatissimi, ma poiché tutta la
produzione viene risparmiata (per compensare il
deprezzamento), il consumo sarà comunque nullo.
e la Regola Aurea
Ne consegue che, fra i due estremi (0/1), esiste un valore critico
di tasso di risparmio che massimizza il consumo/addetto ad un
livello di capitale/addetto di stato stazionario (regola aurea).
Aumenti di capitale oltre il livello di regola aurea porterebbero a
valori più elevati di K/N ma ridurrebbero il consumo (sia nel
breve, sia nel lungo period).
26
Gli effetti del tasso di risparmio sul consumo per
addetto in stato stazionario
Fig. 11. 6. Gli effetti del tasso di risparmio
sul consumo per addetto in stato stazionario.
Un aumento del tasso di risparmio comporta
prima un incremento e poi un calo del consumo
per addetto in stato stazionario.
27
Gli effetti dinamici di un aumento del tasso di risparmio
Effetti dinamici di un aumento del tasso di
risparmio dal 10 al 20% sul livello e sul tasso
di crescita del prodotto per addetto.
L’aumento del tasso di risparmio non
influenza la crescita nel lungo
periodo. Tuttavia fa aumentare il
tasso di crescita del prodotto per un
tempo molto lungo
28