ESAME DI STATO DI LICEO SCIENTIFICO

LICEO SCIENTIFICO
CORSO SPERIMENTALE
SESSIONE ORDINARIA
201 3
Il candidato risolva uno dei due problemi e 5 dei 10 quesiti scelti nel questionario.
2
N. De Rosa, La prova di matematica per il liceo
PROBLEMA1
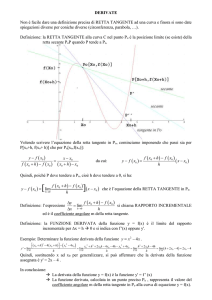
Una funzione f x  è definita e derivabile, insieme alle sue derivate prima e seconda, in
0, e nella figura sono disegnati i grafici  e  di f x  e della sua derivata seconda
f ' ' x  . La tangente a  nel suo punto di flesso, di coordinate (2;4), passa per (0;0),
mentre le rette y  8 e y  0 sono asintoti orizzontali per  e  , rispettivamente.
1. Si dimostri che la funzione f ' x  , ovvero la derivata
prima di f x  , ha un massimo e se ne determinino le
coordinate. Sapendo che per ogni x del dominio è
f ' ' x   f ' x   f x  , qual è un possibile andamento di
f ' x  ?
2. Si supponga che f x  costituisca, ovviamente in
opportune unità di misura, il modello di crescita di una
popolazione. Quali informazioni sulla sua evoluzione si
possono dedurre dai grafici in figura e in particolare dal fatto
che  presenta un asintoto orizzontale e un punto di flesso?
a
3. Se  è il grafico della funzione f x  
, si provi che a  8 e b  2 .
1  e b x
4. Nell’ipotesi del punto 3), si calcoli l’area della regione di piano delimitata da  e
dall’asse x sull’intervallo [0;2].
RISOLUZIONE
Punto 1
Il punto di massimo di f ' x  va ricercato nei punti in cui la sua derivata prima, e cioè f ' ' x  ,
si annulla. Dal grafico di  notiamo che f ' ' x  si annulla in x  2 e che f ' ' x  è positiva in
0,2
e negativa in 2, , pertanto f ' x  è crescente in 0,2 e decrescente in 2, . Di
conseguenza x  2 è l’ascissa di massimo per f ' x  . Per calcolare l’ordinata del massimo,
ricordiamo che f ' x0  rappresenta il coefficiente angolare della retta tangente al grafico di
f x  nel punto ad ascissa x 0 ; poichè la retta tangente a  in (2;4), passa per (0;0), si deduce
che ha equazione y  2 x da cui si ricava che f ' 2  2 . In conclusione il massimo di f ' x 
ha coordinate 2,2 .
Dal grafico  notiamo che f x  è sempre crescente pertanto f ' x   0 x  0, ; inoltre
essendo
verificate
lim f ' x   lim
x 
x 
le
ipotesi
del
teorema
di
De
l’Hopital,
si
ha
f x 
8

 0, da cui lim f ' x   0 il che significa che f ' x  ha la retta
x 
x

y  0 come asintoto orizzontale destro. Dal grafico  si nota che f ' ' x  presenta un
Liceo scientifico sperimentale sessione ordinaria 2013
massimo e un minimo rispettivamente alle ascisse x M e x m , da cui si deduce che la derivata
prima di f ' ' x  o equivalentemente la derivata seconda di f ' x  si annulla nelle suddette
ascisse x M e x m ; di conseguenza la funzione f ' x  presenta due flessi alle ascisse x M e x m ;
inoltre poichè f ' ' x  è crescente in 0, xM   xm , e decrescente in xm , x M  si deduce
che f ' x  è convessa in 0, xM   xm , e concava in xm , x M  .
Di seguito il grafico nello stesso riferimento cartesiano di f x  , f ' x  e f ' ' x  tenendo
conto della resstrizione f ' ' x   f ' x   f x  .
Punto 2
Il fatto che la funzione f presenti un asintoto orizzontale sta a significare che, da un certo
istante di tempo in poi, il numero di componenti la popolazione tende a stabilizzarsi
attorno ad un valore fisso.
A causa del fatto che la derivata prima è sempre positiva, si ha che la funzione è sempre
crescente. Ciò significa che la popolazione è in crescita. La presenza del flesso in x = 2
indica che la rapidità di crescita della popolazione diminuisce: infatti, essendo la derivata
seconda la derivata della derivata prima, si ha che, appena dopo il flesso la derivata prima
(cioè il tasso di crescita di f) inizia a diminuire (pur restando positiva), in quanto la sua
derivata è negativa.
In definitiva, la popolazione ha una crescita accelerata prima del flesso, decelerata dopo lo
stesso.
3
4
N. De Rosa, La prova di matematica per il liceo
Punto 3
Detta f x  
a
la funzione il cui grafico è  , dobbiamo trovare i valori dei parametri
1  e b x
a e b.
Poiché la funzione presenta asintoto orizzontale y  8 , si deve avere lim f x   8 .
x 
Poiché risulta
lim f x   lim
x 
x 
a
a

a
b x
1 e
1  e 
si ha che dev’essere necessariamente a  8 .
La funzione diviene quindi
f x  
8
, bR
1  e b x
Resta da determinare b.
L’informazione che possiamo sfruttare è f ' 2  2, b  R .
Si ha f ' x  
8e b  x
1  e 
b x 2
e poniamola uguale a 2 in x = 2. Risulta
8e b 2
1  e 
b2 2
2
da cui
8e b2  2  2e b2  4e b2 .
Si tratta di una equazione esponenziale nell’incognita reale b.
Posto y  e b2 l’equazione diventa:
8y  2  2y 2  4y ,
da cui
y2  2y 1  0
che ha la soluzione y  1 .
Quindi
e b2  1  b  2  0  b  2
Punto 4
Dobbiamo calcolare l’area delimitata dal grafico della derivata seconda, dall’asse x tra 0 e 2,
di seguito raffigurata.
Liceo scientifico sperimentale sessione ordinaria 2013
Per il significato geometrico dell’integrale definito, essendo la funzione f ' ' positiva su
0,2 , si ha
2
A   f ' ' x dx   f ' x 0  f ' 2  f ' 0.
2
0
Poiché f ' 2  2 , resta da calcolare f ' 0 assumendo come funzione f quella ottenuta
al punto 3.
Si ha f ' x  
8e 2 x
1  e 
2 x 2
da cui f ' 0 
e
8e 2
2

2
1
.
L’area cercata è quindi
A 2
e
8e 2
2

1
2



2
2 e 2  1  8e 2
e
2

1
2
e
2
e
2
2

 1
1
2
2
 1,16.
5
6
N. De Rosa, La prova di matematica per il liceo
PROBLEMA2
Sia f la funzione definita, per tutti gli x positivi da f x   x 3 ln x
1. Si studi f e si tracci il suo grafico  su un piano riferito ad un sistema di assi cartesiani
ortogonali e monometrici Oxy; accertato che  presenta sia un punto di flesso che un
punto di minimo se ne calcolino, con l’aiuto di una calcolatrice, le ascisse arrotondate
alla terza cifra decimale.
2. Sia P il punto in cui  interseca l’asse x. Si trovi l’equazione della parabola, con asse
parallelo all’asse y, passante per l’origine e tangente a  in P.
3. Sia R la regione delimitata da  e dall’asse x sull’intervallo aperto a sinistra ]0;1]. Si
calcoli l’area di R, illustrando il ragionamento seguito, e la si esprima in mm2 avendo
supposto l’unità di misura lineare pari a 1 decimetro.
4. Si disegni la curva simmetrica di  rispetto all’asse y e se ne scriva altresì l’equazione.
Similmente si faccia per la curva simmetrica di  rispetto alla retta y  1 .
RISOLUZIONE
Punto 1
Studiamo della funzione f x   x 3 ln x
Dominio: x  0, ; in realta poichè lim x 3 ln x  0 la funzione è prolungabile per
x 0
 x 3 ln x
continuità in x  0 e si può porre f x   
0
x0
x0
Intersezioni asse ascisse: f x   x ln x  x  0  ln x  0 . Poichè x  0 non appartiene al
3
3
dominio l’unica intersezione si ricava da ln x  0 ed è x  1;
Intersezioni asse ordinate: non ve ne sono in quanto x  0 non appartiene al dominio;
Simmetrie: la funzione non è nè pari nè dispari;
Positività: visto che nel dominio il fattore x 3 è sempre positivo, la funzione è positiva laddove
ln x  0 e quindi per x  1 ed è negativa per 0  x  1 ;
+
+
+
-
x3
ln x
1
x
+
3
Positività: f x   x ln x - Quadro dei segni
0
Asintoti verticali: non ve ne sono in quanto lim x 3 ln x  0 come si deduce applicando il
x 0
1
 x3 
ln x
teorema di de l’Hopital: lim x 3 ln x  lim
 lim x  lim     0 ;
1
3
3 
x 0 
x 0 
x 0 
x 0  
 4
3
x
x
Liceo scientifico sperimentale sessione ordinaria 2013
Asintoti orizzontali: non ve ne sono in quanto lim x 3 ln x   ;
x 
x 3 ln x
 lim x 2 ln x  0 ;
x 
x
x 0 
Asintoti obliqui: non ve ne sono in quanto m  lim
Crescenza e decrescenza: la derivata prima è f ' x   3x 2 ln x  x 2  x 2 3 ln x  1 pertanto la

1
3

1
3
funzione è crescente per x  e e decrescente per 0  x  e e presenta un minimo relativo
1

 1 1 
in  e 3 ,  ; l’ascissa del minimo arrotondata alla terza cifra decimale è xm  e 3  0,717
3e 

1
cui corrisponde una ordinata y m    0,123 ;
3e
x2
3 ln x  1
0
e

1
3
x
Derivata prima: f ' x   x 3 ln x  1 - Quadro dei segni
2
Concavità e convessità: la derivata seconda è
f ' ' x   2 x3 ln x  1  3x  x6 ln x  5
 5

 5 
pertanto la funzione volge concavità verso l’alto in  e 6 ,  e verso il basso in  0, e 6  e




 5 5 5 
presenta un flesso a tangente obliqua in  e 6 , e 2  ; l’ascissa del flesso arrotondata alla
6


5
5

5 2
6
terza cifra decimale è x F  e  0,435 cui corrisponde l’ordinata y F   e  0,068 .
6
x
6 ln x  5
0
e

5
6
x
Derivata seconda: f ' ' x   x6 ln x  5 - Quadro dei segni
Il grafico è di seguito mostrato:
7
8
N. De Rosa, La prova di matematica per il liceo
Punto 2
La parabola richiesta ha equazione y  ax 2  bx . Il passaggio per P(1,0) comporta
0  a  b  b  a
pertanto l’equazione diventa y  ax  x  .
2
La tangente al grafico di f x   x 3 ln x in x  1 ha coefficiente angolare f ' 1  1 ; la tangente
alla parabola in x  1 ha, invece, coefficiente angolare
2ax  ax1  a
pertanto imponendo l’uguaglianza si ricava
a 1
e l’equazione della parabola è pertanto
y  x 2  x .
Di seguito viene presentato nello stesso riferimento cartesiano il grafico di f x   x 3 ln x ,
della parabola e della retta tangente di equazione y  x  1 .
Liceo scientifico sperimentale sessione ordinaria 2013
Punto 3
L’area da calcolare è raffigurata nella figura di seguito.
9
10
N. De Rosa, La prova di matematica per il liceo
Poichè la funzione f x   x 3 ln x è negativa in 0,1 e poichè non è definita in x  0 , l’area
richiesta va calcolata con un passaggio a limite ed è pari a
lim
b 0 
b
1
 x4
x4 
 x ln x dx  lim 
ln x   
b 0
16  b
 4

1
3

 1 b4
b4  1
10000
 lim   ln b    dm 2 
mm 2  625 mm 2
b 0 16
4
16
16
16


in cui si è sfruttata l’integrazione per parti per il calcolo dell’integrale e il limite lim
b 0
b4
ln b  0 .
4
Punto 4
X  x
La simmetrica di f x   x 3 ln x rispetto alla retta x  0 è data dalla trasformazione 
e
Y  y
cioè Y   X 3 ln  X  e ritornando alla simbologia delle coordinate x, y  la simmetrica rispetto
a x  0 ha equazione y   x 3 ln  x  con x  0 .
Liceo scientifico sperimentale sessione ordinaria 2013
Di seguito vengono rappresentate nello stesso riferimento cartesiano la funzione
f x   x 3 ln x e la simmetria y   x 3 ln  x  .
Analogamente la simmetrica rispetto a y  1 si ricava mediante la trasformazione
X  x
e pertanto ha equazione Y  2  X 3 ln X e ritornando anche in questo caso

Y


y

2

alla simbologia delle coordinate x, y 
si ricava che la simmetrica rispetto alla retta
y  1 è y  2  x 3 ln x .
Di seguito vengono rappresentate nello stesso riferimento cartesiano la funzione
f x   x 3 ln x e la simmetria y  2  x 3 ln x con x  0 .
11
12
N. De Rosa, La prova di matematica per il liceo
Liceo scientifico sperimentale sessione ordinaria 2013
13
QUESTIONARIO
Quesito 1
Un triangolo ha area 3 e due lati che misurano 2 e 3. Qual è la misura del
terzo lato? Si giustifichi la risposta.
Le soluzioni al quesito possono essere differenti: ne presentiamo due, la prima che fa uso
della trigonometria e l’altra della geometria.
Uso della trigonometria
L’area di un triangolo è esprimibile come il semiprodotto dei lati per il seno dell’angolo
compreso. Nel caso in esame detto  l’angolo compreso tra i due lati di lunghezza 2 e 3 si
ha: 3 sin   3 da cui sin   1    90 pertanto il triangolo è rettanolo e per il teorema
di Pitagora il terzo lato misura
2 2  32  13 .
Uso della geometria
Si
applica la formula di
A
Erone per il
calcolo dell’area di
p p  a  p  b p  c  ; nel caso in esame il terzo lato c
a  2, b  3 e sil semiperimetro è p 
un triangolo:
è incognito mentre
c5
. Impostando l’equazione A  3 si ottiene:
2
c 5c 5
 c  5
 c  5

 2 
 3 
 c  3

2  2
 2
 2

da cui
c  5  c  1  c  1  5  c 



 3
2  2  2  2 
 25  c 2  c 2  1 


  3
4
4



Elevando al quadrato primo e secondo membro si ha
 25  c 2

 4
 c 2  1 

  9
 4 
ovvero si ottiene l’equazione biquadratica
c 4  26c 2  169  0
equivalente a
c
2

2
 13  0
le cui soluzioni sono
c   13 .
Scartando la soluzione negativa si ritrova il risultato precedentemente trovato, cioè
c  13 .
14
N. De Rosa, La prova di matematica per il liceo
Alternativamente consideriamo il lato di lunghezza 3 come la base del triangolo. Se l’area
deve essere uguale 3 allora l’altezza deve essere pari a 2, ciò significa che l’altro lato di
lunghezza 2 coincide con l’altezza e in quanto tale è perpendicolare al lato di lunghezza 3.
Da ciò si deduce che il triangolo è rettangolo e l’altro lato lo si ricava mediante il teorema
di Pitagora.
Quesito 2 Se la funzione f x   f 2 x ha derivata 5 in x  1 e derivata 7 in x  2 qual
è la derivata di f x   f 4 x  in x  1.
.
Posto g x   f x   f 2 x  , applicando la regola di derivazione delle funzioni composte si
ha
g ' x   f ' x   2 f ' 2 x  . Si sa che g ' 1  5, g ' 2  7 , il che è equivalente a scrivere
f ' 1  2 f ' 2  5 e f ' 2  2 f ' 4  7 .
Risolviamo il sistema
 f ' 1  2 f ' 2  5

 f ' 2  2 f ' 4  7
Moltiplicando ambo i membri della seconda equazione per 2 il sistema diventa
 f ' 1  2 f ' 2  5

2 f ' 2  4 f ' 4  14
e sommando membro a membro le due equazioni si ottiene la condizione
f ' 1  4 f ' 4  19 .
Applicando nuovamente la regola di derivazione delle funzioni composte, posto
hx   f x   f 4 x 
si ha
h' x   f ' x   4 f ' 4 x  ;
calcolando il valore di h' x   f ' x   4 f ' 4 x  in x  1 si ottiene
h' 1  f ' 1  4 f ' 4
che è pari a 19 sfruttando il risultato precedentemente calcolato.
Liceo scientifico sperimentale sessione ordinaria 2013
15
Si considerino nel piano cartesiano i punti A2;1 e B 6;8 . Si
determini l’equazione della retta passante per B e avente distanza massima da A.
Quesito 3
La retta passante per B 6;8 ha equazione y  mx  6  8 e la distanza del punto
A2;1 dalla retta y  mx  6m  8  0 è pari a
7
 7  8m
m

2
8
7  8m  1  m
d m  

.
7
1  m 2  8m  7
m
 1  m 2
8
La derivata prima della funzione distanza è pari a
m

2
  8 1  m  7  8m 
7   7m  83
1  m2


m
8  1  m 2 2
1  m2

d ' m   

m
2
 8 1  m  8m  7 
 7m  8
3

7  1  m 2 2
1  m2
m


8

1  m2
La derivata prima per m 
m
7
8
m
7
8
7
è sempre positiva, pertanto un eventuale distanza massima va
8
7
. In questo caso si nota che la derivata della distanza è positiva per
8
8
8
7
8
m   e negativa per   m  di conseguenza la distanza è massima per m  
7
7
8
7
cui corrisponde la retta
8
48
y x
 8  0  8 x  7 y  104  0
7
7
 8
e una distanza massima pari a d     113 .
 7
ricercata per m 
1  m 
3
2 2
 7m  8

Derivata prima per
7
8
8
7
m
m
7
: d' m  - Quadro dei segni
8
Di seguito un grafico della funzione d m  
7  8m
1  m2
:
16
N. De Rosa, La prova di matematica per il liceo
Alternativamente possiamo ragionare per via geometrica. Consideriamo la figura seguente.
La retta r è la perpendicolare alla retta AB passante per B, mentre la retta s è una ulteriore
retta passante per B e C è il piede della perpendicolare ad essa passante per A.
Liceo scientifico sperimentale sessione ordinaria 2013
Notiamo che il triangolo ACB è rettangolo in C, pertanto AC è un cateto ed in quanto tale
è sempre minore dell’ipotenusa AB. Questo significa che la distanza massima AB la si
ottiene quando B si trova sulla retta perpendicolare ad AB.
y 7
Nel caso in esame la retta AB ha pendenza
 pertanto la perpendicolare ad essa avrà
x 8
y
8
pendenza
  e l’equazione di tale retta perpendicolare passante per B è
x
7
8
y   x  6  8  8 x  7 y  104  0
7
come già precedentemente trovato.
Quesito 4
Di un tronco di piramide retta a base quadrata si conoscono l’altezza h e i
lati a e b delle due basi. Si esprima il volume V del tronco in funzione di a,b e h,
illustrando il ragionamento seguito.
Il tronco assegnato appartiene alla piramide in figura:
Denotiamo con x la distanza del vertice V della piramide dal centro della base superiore
del tronco. In tal modo l’altezza complessiva della piramide risulta h + x.
Per la similitudine dei triangoli VOL e VO’M si ha
h  x  : x  a : b
2 2,
da cui
17
18
N. De Rosa, La prova di matematica per il liceo
x
hb
a b .
L’altezza della piramide di vertice V è quindi
VO  x  h 
hb
a
hh
a b
a b .
Il volume del tronco è quindi uguale al volume dell’intera piramide privato del volume
della piramide di vertice V e avente per base la base superiore del tronco.
Si ha quindi



1  ha  1 2  hb  1 h
1
V  a2 
a 3  b 3  h a 2  b 2  ab
 b 

3  a  b  3  a  b  3 a  b 
3

Quesito 5
In un libro si legge: “se per dilatazione corrispondente a un certo aumento
della temperatura un corpo si allunga (in tutte le direzioni) di una certa percentuale (p.es
0,38%), esso si accresce in volume in proporzione tripla (cioè dell’1,14%), mentre la sua
superficie si accresce in proporzione doppia (cioè di 0,76%)”. E’ così? Si motivi
esaurientemente la risposta.
Consideriamo un corpo imogeneo e isotropo a forma di parallelepipedo di dimensioni
lineari a, b, c il cui volume è V  abc e sia  la percentuale di dilatazione del corpo a
seguito di aumento della temperatura. Il valore  va sotto il nome di coefficiente di
dilatazione lineare.
Con l’aumento della temperatura le sue dimensioni saranno
a1  a  a  a1   

b1  b  b  b1   
c  c  c  c1   
 1
pertanto il nuovo volume sarà V1  a1b1c1  1    abc .
3
Il valore 1    è pari a 3  32  3  1 , pertanto l’incremento di volume sarà pari a
3
V1  V
 3  32  3
V
Poichè di norma il coefficiente di dilatazione lineare è molto piccolo, allora si possono
trascurare i termini cubico e quadratico 3 e 32 ed affermare con un buon grado di
precisione che l’incremento di volume è pari a
V1  V
 3
V
Liceo scientifico sperimentale sessione ordinaria 2013
cioè il volume si accresce in proporzione tripla, il che significa che il coefficiente di
dilatazione volumica è il triplo di quello lineare.
A livello di superficie, considerando una superficie di lati a e b, a seguito di dilatazione i
lati saranno
a1  a  a  a1   

b1  b  b  b1   
pertanto la nuova superficie sarà S1  a1b1  1    ab .
2
Il valore 1    è pari a 2  2  1 , pertanto l’incremento di superficie sarà pari a
2
S1  S
 2  2
S
Poichè di norma il coefficiente di dilatazione lineare è molto piccolo, allora si può
trascurare il termine quadratico 2 ed affermare con un buon grado di precisione che
l’incremento di volume è pari a
S1  S
 2
S
cioè la superficie si accresce in proporzione doppia, il che significa che il coefficiente di
dilatazione superficiale è il doppio di quello lineare.
In conclusione la risposta è corretta a patto che si consideri un coefficiente di dilatazione
lineare molto piccolo.
Quesito 6
Con le cifre da 1 a 7 è possibile formare 7!=5040 numeri corrispondenti
alle permutazioni delle 7 cifre. Ad esempio i numeri 1234567 e 3546712 corrispondono a
due di queste permutazioni. Se i 5040 numeri ottenuti si dispongono in pridne crescente
qual è il numero che occupa la 5036-esima posizione e quale quello che occupa la 1441esima posizione?
Disponiamo in ordine decrescente i numeri dalla 5040-esima alla 5036-esima posizione. Di
seguito una tabellina riassuntiva:
Numero
7654321
7654312
7654231
7654213
7654132
Posizione
5040-esima
5039-esima
5038-esima
5037-esima
5036-esima
da cui deduciamo che il numero in 5036-esima posizione è 7654132.
19
20
N. De Rosa, La prova di matematica per il liceo
Fissando la prima cifra, si possono avere 6!=720 combinazioni di sei numeri che assieme
alla prima cifra formano un numero di 7 cifre. Questo significa che fissato 1 come prima
cifra si hanno 720 numeri di 7 cifre che iniziano con 1 mentre dall 721° al 1440° abbiamo
numeri di 7 cifre che iniziano con 2. Pertanto il 1441° numero è il primo numero che inizia
con 3 e cioè 3124567.
Quesito 7
In un gruppo di 10 persone il 60% ha gli occhi azzurri. Dal gruppo si
selezionano a caso due persone. Quale è la probabilità che nessuna di essi abbia gli occhi
azzurri?
4
; selezionata la
10
prima persona, la probabilità che anche la seconda non abbia gli occhi azzurri è pari a
3
p 2  pertanto la probabilità che nessuna delle due abbia gli occhi azzurri è dato dal
9
prodotto delle due probabilità
4 3 2
p1  p 2   
10 9 15
Alternativamente per risolvere il quesito possiamo far uso del concetto di combinazione.
Date 10 persone il numero di combinazioni di persone prese due alla volta è
10  10  9
C10, 2    
 45
 2  2 1
Il numero di combinazioni di coppie di persone che non ha gli occhi azzurri è pari a
La probabilità che una persona su 10 non abbia gli occhi azzurri è p1 
 4 4  3
C 4, 2    
6
 2  2 1
La probabilità richiesta è pertanto data dal rapporto tra i casi favorevoli e i casi totali e cioè
 4
 
C 4, 2
2
6
2
   

C10, 2 10  45 15
 
2
come già trovato.
Quesito 8 Si mostri, senza utilizzare il teorema di l’Hopital, che:
lim
x 
e sin x  e sin 
x 
Il limite si presenta chiaramente nella forma indeterminata
notevoli, operiamo una sostituzione.
Poniamo
x   t .
0
. Per poter ricorrere ai limiti
0
Liceo scientifico sperimentale sessione ordinaria 2013
Si ha chiaramente
t 0
e
x  t .
Per il teorema di sostituzione e a causa della formula sugli archi associati
( sin      sin  ), il limite diviene
lim
t 0
e sin t   1
e  sin t  1
.
 lim
t 0
t
t
In forza del limite notevole
e y 1
1,
y 0
y
e dei teoremi dei limiti (il limite di un prodotto è uguale al prodotto dei limiti), posto
y   sin t ,
abbiamo
 e  sin t  1

e  sin t  1
e  sin t  1
 sin t
lim
 lim 
  sin t   lim
 lim
 1   1  1 .
t 0
t o (  sin t )  t
t

 t 0  sin t t 0 t
Alternativamente basta notare che il limite richiesto non è altro che la derivata della funzione
f x   e sin x in x   . Poichè la derivata prima è pari a f ' x   cos x  e sin x si ha
lim
e sin x  e sin 
 f '    cos   e sin   1  e 0  1  1  1
x 
x 
lim
Quesito 9
Tre amici discutono animatamente di numeri reali. Anna afferma che sia i
numeri razionali che gli irrazionali sono infiniti e dunque i razionali sono tanti quanti gli
irrazionali. Paolo sostiene che gli irrazionali costituiscono dei casi eccezionali, ovvero che
la maggior parte dei numeri reali sono razionali. Luisa afferma, invece, il contrario: sia i
numeri razionali che gli irrazionali sono infiniti, ma esistono più numeri irrazionali che
razionali. Chi ha ragione? Si motivi esaurientemente la rsposta.
Ricordiamo un teorema: dati due insiemi di cui A con la potenza superiore al numerabile e
B con potenza del numerabile, l’insieme differenza A-B ha la potenza superiore al
numerabile.
Nel caso in esame consideriamo l’insieme A come l’insieme dei numeri reali R che ha la
potenza del continuo; consideriamo, invece, B come l’insieme dei numeri razionali Q che
ha la stessa potenza numerabile dell’insieme dei numeri naturali N. Pertanto l’insieme
differenza R-Q, che non è altro che l’insieme dei numeri irrazionali, ha la stessa potenza di
R e cioè superiore al numerabile. Ciò significa che i numeri irrazionali sono in numero
maggiore rispetto ai razionali e Luisa ha ragione.
Quesito 10 Si stabilisca per quali valori di k  R l’equazione x 2 3  x   k ammette
due soluzioni distinte appartenenti all’intervallo [0,3]. Posto k  3 , si approssimi con due
cifre decimali la maggiore di tali soluzioni, applicando uno dei metodi iterativi studiati.
Lo studio dell’equazione x 2 3  x   k può essere condotto per via grafica risolvendo il
seguente sistema
21
22
N. De Rosa, La prova di matematica per il liceo
 y  x 2 3  x 

y  k
il che significa discutere graficamente le intersezioni della cubica di equazione y  x 2 3  x  con
la retta parallela all’asse delle ascisse di equazione y  k .
La cubica y  x 2 3  x 

interseca l’asse delle ascisse in x  0  x  3

è positiva in  ,0  0,3

ha derivata prima y'  6 x  3x 2 pertanto è crescente in 0,2 e decrescente in
 ,0  2, e presenta un minimo in 0,0 e un massimo in 2,4

ha derivata seconda y' '  6  6 x pertanto volge concavità verso l’alto in  ,1 e
verso il basso in 1, e presenta un flesso a tangente obliqua in 1,2 .
Di seguito vengono presentati nello stesso riferimento cartesiano il grafico della cubica
y  x 2 3  x  e la retta y  k .
Liceo scientifico sperimentale sessione ordinaria 2013
23
Dal grafico si nota che nell’intervallo [0,3] l’equazione x 2 3  x   k presenta due
soluzioni distinte per 0  k  4 di cui la maggiore è maggiore di 2 in quanto alla destra
dell’ascissa di massimo.
Posto k  3 , si deve risolvere l’equazione x 2 3  x   3 o equivalentemente trovare la
radice della funzione
h2  1, h3  3
hx   x 3  3x 2  3 . Consideriamo l’intervallo [2,3]. Si ha
pertanto h2  h3  0 il che conferma che la radice appartiene
all’intervallo (2,3). Inoltre la derivata prima è h' x   3x 2  6 x e la derivata seconda
h' ' x   6 x  6 , ed essendo quest’ultima positiva in [2,3], è possibile applicare il metodo
delle tangenti o di Newton-Raphson per il calcolo dell’unica radice   2,3 con punto
iniziale x0  3 in quanto h3  h' ' 3  0 attraverso la seguente formula di ricorrenza:
xn1  xn 
h x n 
x 3  3x 2  3 2 xn3  3xn2  3
 xn  n 2 n

h'  x n 
3x n  6 x n
3xn2  6 xn
Di seguito una tabella che riassume i vari passi dell’algoritmo.
n
xn
xn 1
 n  xn  xn1
0
1
2
3
4
3,0000
2,6667
2,5486
2,5324
2,5321
2,6667
2,5486
2,5324
2,5321
2,5321
0,333
0,118
0,016
0,000
n 
1
100
NO
NO
NO
SI
da cui deduciamo che la radice cercata è   2,53 .
Alternativamente avremmo potuto applicare il metodo di bisezione. Di seguito una tabella
che ne evidenzia tutti i passi.
n
a
b
0
1
2
3
4
5
6
7
8
2,00000
2,50000
2,50000
2,50000
2,50000
2,53125
2,53125
2,53125
2,53125
3,00000
3,00000
2,75000
2,62500
2,56250
2,56250
2,54688
2,53906
2,53516
ab
2
2,50000
2,75000
2,62500
2,56250
2,53125
2,54688
2,53906
2,53516
2,53320
m
f a 
-1,00000
-0,12500
-0,12500
-0,12500
-0,12500
-0,00339
-0,00339
-0,00339
f b 
f m
3,00000 -0,12500
3,00000 1,10938
1,10938 0,41602
0,41602 0,12720
0,12720 -0,00339
0,12720 0,06077
0,06077 0,02841
0,02841 0,01244
  ba 
NO
NO
NO
NO
NO
NO
NO
SI
1
100
24
N. De Rosa, La prova di matematica per il liceo
Dalla tabella soprastante deduciamo, come già trovato, che la radice richiesta, con due cifre
decimali esatte, è   2,53 .
Notiamo che il metodo delle tangenti o di Newton-Raphson ha una velocità di convergenza
maggiore rispetto al metodo di bisezione, e che fornisce anche una stima migliore rispetto
al metodo dicotomico. Infatti il metodo di Newton-Raphson in 4 iterazioni permette di
calcolare la radice con 3 cifre decimali esatte, mentre il metodo di bisezione consente di
calcolare in 7 iterazioni solo una stima con 2 cifre decimali esatte.
Anche se non espressamente richiesto, con il metodo iterativo di bisezione, calcoliamo la
minore delle due radici   0,2 . Di seguito una tabella che ne evidenzia tutti i passi.
n
a
b
0
1
2
3
4
5
6
7
8
9
2,00000
2,00000
1,50000
1,50000
1,37500
1,37500
1,37500
1,35938
1,35156
1,34766
0,00000
1,00000
1,00000
1,25000
1,25000
1,31250
1,34375
1,34375
1,34375
1,34375
ab
2
1,00000
1,50000
1,25000
1,37500
1,31250
1,34375
1,35938
1,35156
1,34766
1,34570
m
f a 
f b 
f m
-1,00000
-1,00000
-0,37500
-0,37500
-0,07227
-0,07227
-0,07227
-0,03171
-0,01124
3,00000
1,00000
1,00000
0,26563
0,26563
0,09302
0,00937
0,00937
0,00937
1,00000
-0,37500
0,26563
-0,07227
0,09302
0,00937
-0,03171
-0,01124
-0,00095
  ba 
1
100
NO
NO
NO
NO
NO
NO
NO
NO
SI
Dalla tabella soprastante deduciamo, come già trovato, che la radice richiesta, con due cifre
decimali esatte, è   1,34 .