- I.I.S. Prever – Pinerolo

Capitolo 1
Insiemi numerici: proprietà e operazioni
1.1. Proprietà dell’insieme dei naturali
L’insieme dei numeri naturali è costituito dai numeri interi positivi e dallo zero. I numeri naturali
sono una costruzione della mente umana suggerita dalla realtà fisica. A questo proposito citiamo a
titolo emblematico le parole del matematico tedesco Leopold Kronecker: "Dio fece i numeri
interi(naturali); tutto il resto è opera dell'uomo” (il grassetto è mio). Essi vengono concepiti per
poter enumerare insiemi di oggetti interi. L’insieme dei numeri interi si indica con la lettera N ed
espresso in modo esplicito coincide con l’insieme 0,1,2,3,4,.....
Proprietà 1.1.1
N è infinito. Per verificare tale affermazione basta pensare che dato il numero naturale 0 per
ottenere i numeri naturali successivi basta aggiungere ad esso viepiù 1. Pensate un numero naturale
grande a piacere. È possibile trovare un numero naturale più grande aggiungendo ad esso un
qualsiasi numero naturale più grande di 0.
Proprietà 1.1.2
N è ordinato nel senso che dati due numeri naturali distinti è sempre possibile stabilire qual è il più
grande dei due. In ragione di ciò è possibile ordinarli dal più piccolo al più grande. Riportiamo qui
di seguito la distribuzione dei numeri naturali sulla retta reale.
Proprietà 1.1.3.
N è discreto nel senso che dati due numeri naturali distinti tra loro compaiono soltanto un numero
finito di numeri naturali.
Autore: Siano Roberto (docente di Matematica presso l’I.I.S. Arturo Prever di Pinerolo)
1.2. Operazioni nell’insieme dei numeri naturali
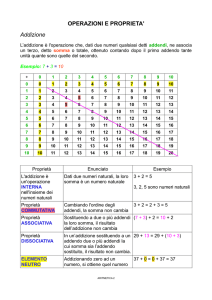
Definizione 1.2.1 (di addizione)
Dati due numeri naturali a e b, si definisce somma di a e b il numero naturale ottenuto
addizionando ad a il numero naturale 1 b volte. In simboli: a  b  a  1

1
 ...

1 . La suddetta
bvolte
operazione prende il nome di addizione e i suoi termini di addendi.
Proprietà dell’addizione
Proprietà 1.2.1(commutativa)
Se si cambia l’ordine degli addendi la somma non cambia. In simboli: a  b  b  a , per ogni a, b 
N.
Esempio 1.2.1
23  3 2
Proprietà 1.2.2(associativa)
Per addizionare tre numeri naturali occorre effettuare due addizioni successive. È possibile
procedere addizionando alla somma dei primi due il terzo oppure addizionando alla somma degli
ultimi due il primo. La proprietà associativa stabilisce che tali modi di procedere sono del tutto
equivalenti. In simboli: (a  b)  c  a  (b  c)  a  b  c , per ogni a, b, c N.
Proprietà 1.2.2(esistenza dell’elemento neutro)
Esiste un numero naturale ( lo zero) che addizionato ad un qualunque numero naturale dà come
risultato il numero naturale stesso. In simboli: a  0  0  a  a , per ogni a N.
Definizione 1.2.2 ( di sottrazione)
Dati due numeri naturali a e b (con a  b ), si definisce differenza tra a e b il numero naturale che
addizionato a b dà a. In simboli: a  b  c , dove c  b  a . La suddetta operazione prende il nome
di sottrazione, il suo primo termine prende il nome di minuendo ed il secondo di sottraendo.
Proprietà della sottrazione
Proprietà 1.2.3(invariantiva)
La differenza non varia se si addizionano o si sottraggono opportunamente al minuendo e al
sottraendo lo stesso numero naturale. In simboli: a  b  a  c  b  c , per ogni a, b, c N e
a  b  a  c  b  c , per ogni a, b, c N tali che a  c e b  c .
Autore: Siano Roberto (docente di Matematica presso l’I.I.S. Arturo Prever di Pinerolo)
Esempio 1.2.2
7  4  3  7  5  4  5  12  9
7  4  3  7  3  4  3  4  1
Osservazione 1.2.1
Per comprendere l’operazione di addizione basta pensare all’operazione insiemistica di unione.
L’addizione di due numeri naturali può essere vista come l’operazione che permette di enumerare
gli oggetti di un insieme dato come unione di due insiemi contenenti oggetti distinti.
Osservazione 1.2.2
Dalle definizioni fornite risulta evidente il fatto che la sottrazione è l’operazione inversa
dell’addizione nel senso che per poter determinare la differenza tra due numeri naturali è necessario
effettuare un numero finito di addizioni fra il sottraendo e i numeri naturali a partire dallo 0 fino a
che non si raggiunge il valore del minuendo.
Osservazione 1.2.3
È facile verificare che l’addizione è un’operazione chiusa in N. In altri termini dati due numeri
naturali qualunque la loro somma è ancora un numero naturale. Per contro la sottrazione è aperta in
N perché se si prende un minuendo minore di un sottraendo non si ottiene alcun numero naturale
ragion per cui sarà necessario nel seguito introdurre un ulteriore insieme numerico.
Definizione 1.2.3
Dati due numeri naturali a e b, si definisce prodotto di a e b il numero naturale ottenuto
a  ...
 a . La suddetta operazione prende
addizionando a a se stesso b volte. In simboli: a  b  a



bvolte
il nome di moltiplicazione e i suoi termini di fattori.
Osservazione 1.2.3
Precisiamo che la moltiplicazione può essere intesa come un’addizione i cui addendi sono tutti
uguali.
Proprietà della moltiplicazione
Proprietà 1.2.4(commutativa)
Scambiando l’ordine dei fattori il prodotto non cambia. In simboli: a  b  b  a , per ogni a, b  N.
Autore: Siano Roberto (docente di Matematica presso l’I.I.S. Arturo Prever di Pinerolo)
Esempio 1.2.3
5  3  3  5  15
Proprietà 1.2.5(associativa)
Per moltiplicare tre numeri naturali occorre effettuare due moltiplicazioni successive. È possibile
procedere moltiplicando il prodotto dei primi due il terzo oppure moltiplicando il prodotto degli
ultimi due il primo. La proprietà associativa stabilisce che tali modi di procedere sono del tutto
equivalenti. In simboli: (a  b)  c  a  (b  c)  a  b  c , per ogni a, b, c N.
Esempio 1.2.4
2  5  7  10  7  70  2  5  7  2  35
Proprietà 1.2.6(distributiva a sinistra rispetto all’addizione)
La moltiplicazione di un numero naturale per una somma di numeri naturali fornisce lo stesso
risultato che fornirebbe la somma del prodotto di tale numero per ciascun addendo. In simboli:
a  b  c  a  b  a  c , per ogni a, b, c N.
Esempio 1.2.5
4  5  3  4  8  32  4  5  4  3  20  12
Proprietà 1.2.7(distributiva a destra rispetto all’addizione)
La moltiplicazione della somma di due numeri naturali per un numero naturale fornisce lo stesso
risultato che fornirebbe la somma del prodotto di ciascun addendo per il numero. In simboli:
b  c  a  b  a  c  a , per ogni a, b, c N.
Esempio 1.2.5
5  3  4  8  4  32  5  4  3  4  20  12
Situazione concreta che permette d’illustrare il contenuto della proprietà distributiva della
moltiplicazione rispetto all’addizione
5 ragazzi si sono recati dapprima in panetteria e ciascuno di loro ha speso 7 €, successivamente in
cartoleria e ciascuno di loro ha speso 9 €. Ci si chiede quale sia la loro spesa totale. È evidente che
il calcolo della spesa si può ottenere in due modi differenti, ma equivalenti dal punto di vista del
risultato. Facendo uso dell’aritmetica si ha che: 7  9  5  7  5  9  5 .
Autore: Siano Roberto (docente di Matematica presso l’I.I.S. Arturo Prever di Pinerolo)
Proprietà 1.2.8(distributiva a sinistra rispetto alla sottrazione)
La moltiplicazione di un numero naturale per la differenza di due numeri naturali fornisce lo stesso
risultato che fornirebbe la differenza del prodotto di tale numero per ciascun termine della
sottrazione. In simboli: a  b  c  a  b  a  c , per ogni a, b, c  N, b  c .
Esempio 1.2.6
4  5  3  4  2  8  4  5  4  3  20  12
Proprietà 1.2.9(distributiva a destra rispetto alla sottrazione)
La moltiplicazione della differenza di due numeri naturali per un numero naturale fornisce lo stesso
risultato che fornirebbe la differenza del prodotto di ciascun termine della sottrazione per il numero.
In simboli: b  c  a  b  a  c  a , per ogni a, b, c N, b  c .
Esempio 1.2.7
5  3  4  2  4  8  5  4  3  4  20  12
Situazione concreta che permette d’illustrare il contenuto della proprietà distributiva della
moltiplicazione rispetto alla sottrazione
5 ragazzi si sono recati dapprima in panetteria e ciascuno di loro ha speso 3 €, successivamente il
padre di uno di loro regala a ciascuno di essi 9 €. Ci si chiede quale sia la situazione contabile
complessiva di tutti i ragazzi. È evidente che il calcolo della spesa si può ottenere in due modi
differenti, ma equivalenti dal punto di vista del risultato. Facendo uso dell’aritmetica si ha che:
9  3  5  9  5  3  5 .
Proprietà 1.2.10(esistenza dell’elemento neutro)
Esiste un numero naturale ( l’uno) che moltiplicato per un qualunque numero naturale dà come
risultato il numero naturale stesso. In simboli: a  1  1 a  a , per ogni a N.
Osservazione 1.2.4
Autore: Siano Roberto (docente di Matematica presso l’I.I.S. Arturo Prever di Pinerolo)
Si precisa che prende il nome di aritmetica quella branca della matematica che si occupa dei numeri
naturali e delle loro operazioni. Il termine aritmetica deriva dal termine greco αριτμός (leggi:
aritmòs) che significa numero.
Proprietà 1.2.11(esistenza dell’elemento annullatore)
Esiste un numero naturale ( lo zero) che moltiplicato per un qualunque numero naturale dà come
risultato lo zero. In simboli: a  0  0  a  0 , per ogni a N.
Proprietà 1.2.12(legge di annullamento del prodotto)
Se il prodotto di due numeri naturali a e b è uguale a 0, allora è possibile trarre delle conclusioni sui
due numeri. In altri termini, si può presentare una delle situazioni seguenti:



a0 e b0
b0 e a0
ab0
Definizione 1.2.4
Dati due numeri naturali a e b, si definisce quoziente di a e b il numero naturale c che moltiplicato
per b fornisce a . In simboli: a : b  c , dove c  b  a . La suddetta operazione prende il nome di
divisione, il suo primo termine prende il nome di dividendo ed il suo secondo termine di divisore.
Osservazione 1.2.5
Per comprendere il significato di moltiplicazione basta pensare alla situazione concreta in cui si
dispone di un numero di oggetti (delle caramelle per esempio) e si intende dividerlo per un certo
numero di persone in modo tale che ognuna di esse disponga a seguito della distribuzione dello
stesso numero di oggetti. Si vede facilmente che non sempre è possibile raggiungere l’obiettivo.
Inoltre è palese il fatto che per eseguire occorre effettuare un opportuno numero di moltiplicazioni.
Facciamo un esempio per comprendere quanto detto. Per trovare il risultato della divisione 6 : 2 è
necessario moltiplicare il divisore, nella fattispecie 2, successivamente, per tutti i numeri naturali
che vanno dall’1 in poi, finché non si ottiene il numero 6. Il numero che moltiplicato per 2 dà 6
(che è 3) è il risultato della divisione.
Osservazione 1.2.6
Come mostra l’osservazione precedente la divisione, a differenza della moltiplicazione, non è
un’operazione chiusa in quanto la divisione di due numeri naturali non sempre dà un numero
naturale, ragion per cui sarà necessario nel seguito introdurre un ulteriore insieme numerico e
parlare di divisione con resto nell’insieme dei numeri naturali.
Osservazione 1.2.7
Autore: Siano Roberto (docente di Matematica presso l’I.I.S. Arturo Prever di Pinerolo)
Precisiamo che la divisione per 0 non si può eseguire. Infatti 5 : 0 è il numero che moltiplicato per 0
dà 5, ma 0 moltiplicato per un qualsiasi numero dà sempre 0 e non darà mai 5. L’operazione risulta ,
quindi, impossibile. Infine la divisione 0 : 0 si dice indeterminata intendendo che tale operazione ha
infiniti risultati. Infatti 0 : 0 è il numero che moltiplicato per 0 da 0, ma tutti i numeri soddisfano a
tale richiesta.
Proprietà della divisione
Proprietà 1.2.13 (proprietà invariantiva)
Il risultato di una divisione non cambia (varia, da cui la parola invariantiva) se si moltiplicano o se
si dividono il dividendo e il divisore per lo stesso numero naturale. In simboli:
a : b  a  c : b  c , per ogni a, b, c N, dove a  b e b  0
a : b  a : c : b : c , per ogni a, b, c N, dove a  b  c e b, c  0
Esempio 1.2.8
18 : 9  2  18  3 : 9  3  54 : 27
18 : 9  2  18 : 3 : 9 : 3  6 : 3
Proprietà 1.2.14 (proprietà distributiva a destra rispetto all’addizione)
a  b : c  a : c  b : c , per ogni
a, b, c N, dove a, b  c e c  0
Esempio 1.2.9
9  6 : 3  5  9 : 3  6 : 3  3  2
Proprietà 1.2.14 (proprietà distributiva a destra rispetto alla sottrazione)
a  b : c  a : c  b : c , per ogni
a, b, c N, dove a, b  c e c  0
Esempio 1.2.10
9  6 : 3  1  9 : 3  6 : 3  3  2
Osservazione 1.2.8
Autore: Siano Roberto (docente di Matematica presso l’I.I.S. Arturo Prever di Pinerolo)
Si precisa che la proprietà distributiva a sinistra non vale né per l’addizione, né per la sottrazione.
Si consideri a tal fine il seguente esempio:
12 : 4  2  2  12 : 4  12 : 2  3  6  9
1.3. Divisione con resto
Definizione 1.3.1 (di divisione con resto)
Dati due numeri naturali a e b, si definiscono quoziente e resto della divisione tra a e b il numero
naturale c e il numero naturale r tali che c  b  r  a . La suddetta operazione prende il nome di
divisione con resto.
Esempio 1.3.1
7 : 2  3 con il resto di 1. Infatti 3  2  1  7 .
Osservazione 1.3.1
La suddetta operazione si introduce perché non tutte le divisioni tra numeri naturali danno come
risultato un numero naturale. L’introduzione di tale operazione può tornare utile sia in situazioni
concrete, sia nell’ambito di alcune procedure come la determinazione del M.C.D. (massimo comun
divisore) di due numeri naturali con l’algoritmo di Euclide.
1.4. Multipli e divisori
Definizione 1.4.1 (di multiplo)
Dato un numero naturale a si dice che il numero naturale b è un multiplo di a se b  a  n , dove n è
un numero naturale qualunque.
Osservazione 1.4.1
In altri termini: i multipli di a si trovano moltiplicando a per un numero naturale n qualunque. Si
precisa che tra i multipli di un numero naturale qualunque c’è anche 0, che risulta essere multiplo di
tutti i numeri naturali. In pratica, però, come vedremo in seguito nel contesto della determinazione
Autore: Siano Roberto (docente di Matematica presso l’I.I.S. Arturo Prever di Pinerolo)
del m.c.m. (minimo comune multiplo) lo zero non viene annoverato fra i multipli dei numeri
naturali.
Esempio 1.4.1
I multipli di 5 si ottengono moltiplicando 5 per un numero naturale qualunque. In tal caso si
ottengono i numeri contenuti nella tabellina del 5.
50  0
5 1  5
5  2  10
5  3  15
5  4  20
.
Definizione 1.4.2 (di divisore)
Dato un numero naturale a si dice che il numero naturale b  0 è un divisore di a se a : b  c , dove
c è un numero naturale diverso da 0.
Osservazione 1.4.2
Faccio notare che la definizione di multiplo e di divisore sono strettamente legate, in quanto se un
numero naturale a è multiplo di un numero naturale b, allora b è un divisore di a. Inoltre se b è un
divisore di a, allora a è un multiplo di b.
Osservazione 1.4.3
Si precisa che 0 non è divisore di alcun numero perché la divisione per 0 o non dà risultato o è
indeterminata.
Definizione 1.4.2 (di divisibilità)
Se un numero naturale b  0 è un divisore di a si dice anche che a è divisibile per b.
1.5. Numeri primi
Definizione 1.5.1 (di numero primo)
Un numero naturale p si dice primo se è divisibile soltanto per sé stesso e per 1.
Osservazione 1.5.1
Autore: Siano Roberto (docente di Matematica presso l’I.I.S. Arturo Prever di Pinerolo)
Faccio notare che tutti i numeri sono divisibili per sé stessi e per 1, ma i numeri primi sono
divisibili soltanto per sé stessi e per 1.
Osservazione 1.5.2
Faccio notare che un numero è primo quando è multiplo soltanto di sé stesso e di 1. Con un
linguaggio più vicino al mondo della scuola primaria si potrebbe dire che un numero è primo se sta
soltanto nella sua tabellina e in quella dell’1.
Esempio 1.5.1
I numeri 3, 5 e 7 sono primi.
Quanti sono i numeri primi?
La risposta a tale importante domanda è fornita dal seguente
Teorema 1.5.1 (Teorema di Euclide)
I numeri primi sono infiniti
Dimostrazione
Si consideri il numero
Autore: Siano Roberto (docente di Matematica presso l’I.I.S. Arturo Prever di Pinerolo)