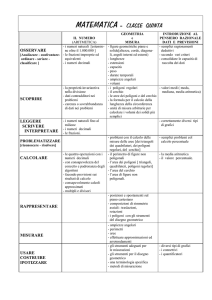
MESSA A PUNTO DI UNA SITUAZIONE – PROBLEMA
Per superare i limiti della “pedagogia per obiettivi”, elaborata in un
contesto
culturale
sostanzialmente
neo
comportamentista,
bisogna
focalizzare l’attenzione sui rapporti tra i soggetti didattici: il sapere,
l’insegnante e l’allievo, nell’ambito della “Teoria
delle
situazioni”,
elaborata da Guy Brousseau.
Il ruolo dell’insegnante è quello di mediare la conoscenza, quella di uno
specifico ambiente, e le esigenze degli allievi, costruendo i propri percorsi
di insegnamento/apprendimento e operando delle scelte motivate e con
giustificazioni epistemologiche.
Per
operare
delle
scelte
significative,
in
rapporto
a
contenuti,
competenze, attività e verifiche, l’analisi a priori potrebbe essere uno
strumento efficace.
Ricordando che l’obiettivo della situazione a-didattica ipotizzata è quello
di far acquisire operativamente, tramite un tipo di apprendimento per
scoperta che parte dalle congetture degli studenti, il concetto di
equivalenza, abbiamo messo a punto una situazione problema inerente a
tale tematica, che implica l’esercizio di capacità di analisi, sintesi ed
ottimizzazione delle soluzioni.
Il testo della situazione – problema è il seguente:
Vogliamo ricoprire il pavimento del parco giochi della scuola con
una guaina di gomma.
Sappiamo che il parco giochi è di forma rettangolare ed ha come
dimensioni 3 m e 4 m.
Nei negozi, però, la guaina è disponibile solo in rotoli di 2 m di
larghezza, allora quanto misurerà in lunghezza ogni pezzo?
Per quanto riguarda l’analisi epistemologica del concetto di Equivalenza
nel piano, riportiamo quanto espresso nell’Enciclopedia delle Matematiche
Elementari e Complementi (L. Berzolari- G. Vivanti- D.Gigli, Enciclopedia
delle Matematiche Elementari e Complementi, Hoepli, Milano, 1979).
Capitolo XXII PROPRIETA’ ELEMENTARI DELLE FIGURE DEL PIANO E DELLO
SPAZIO
21. Equivalenza di poligoni piani.
Il concetto di uguaglianza di estensione, acquisito fin dai tempi più antichi, fermò ben
presto l’attenzione degli studiosi su questioni geometriche, anzi, come si può arguire
dalla parola, la geometri nacque dal confronto di estensioni di terreno.
L’importanza data a tali questioni risulta palese non solo dalle notizie che abbiamo
sulla scienza egiziana, ma anche dal fatto che la scuola di Pitagora si occupò
specialmente di quella parte della geometria che oggi si chiama Teoria dell’equivalenza;
anzi tale indirizzo trapela ancora nella geometria di Euclide.
Ma, perché l’eguaglianza di estensione, nel senso intuitivo della frase, possa essere
oggetto di studio rigoroso, è necessaria un’analisi approfondita, che manca in Euclide,
e fu compiuta soltanto in tempi recenti.
Due poligoni piani si dicono Equivalenti se sono scomponibili in poligoni rispettivamente
uguali.
Poiché due poligoni uguali sono scomponibili in triangoli uguali per mezzo delle diagonali
uscenti da due vertici corrispondenti, la definizione precedente può anche enunciarsi
dicendo che sono equivalenti due poligoni scomponibili in triangoli uguali.
L’equivalenza gode della proprietà riflessiva, simmetrica e transitiva.
Capitolo XXI FONDAMENTI DI GEOMETRIA
Equivalenza nel piano e nello spazio
41. Scomponibilità di poligoni in parti rispettivamente uguali e questioni relative.
1. La teoria euclidea dell’equivalenza (o uguaglianza di area) dei poligoni si fonda su
alcuni principi o postulati che qui enunciamo con la nomenclatura moderna:
1. Poligoni uguali sono equivalenti;
2. Poligoni equivalenti ad uno stesso sono equivalenti tra loro;
3. Somme di poligoni equivalenti sono equivalenti sono equivalenti;
4. Differenze di poligoni equivalenti sono equivalenti;
5. Un poligono non è equivalente ad una sua parte.
Ma il concetto di Area rimane primitivo; così per i geometri successivi fino ad A. M.
Legendre, R. Baltzer, A. Amiot e per lo stesso A. Faifofer, cui pure spetta il merito di
aver rinnovato, didatticamente, questa teoria.
2. Dallo stesso svolgimento di Euclide, che si può modificare in modo da evitare
l’applicazione del 4°principio, risulta che due poligoni equivalenti sono sempre
decomponibili in parti poligonali rispettivamente uguali; e poiché inversamente poligoni
composti di parti rispettivamente uguali sono equivalenti per i principi 1° e 3°, si
traggono due conclusioni: che la relazione di equivalenza è sufficientemente
determinata dai postulati 1, 2, 3, 5; che si può eliminare il concetto primitivo di area,
sostituendolo con una definizione fondata sull’equiscomponibilità.
Così facendo, le proprietà espresse dai postulati 1, 2, 3 divengono subito corollari
della definizione o teoremi; la proprietà espressa dal principio 5° invece resiste e per
vario tempo rimase dubbio se essa dovesse essere conservata come postulato.
3. In un primo periodo, però, tale questione non fu sollevata.
Fu A. De Zolt a osservare come, nella nuova teoria dell’equivalenza, fosse rimasto un
principio intuitivo che egli enunciò in questa forma: Scomposto un poligono in parti non
si può con esse meno una ricomporre il poligono primitivo.
Ma è questo un postulato o un teorema?
A.DE ZOLT stesso proponeva una dimostrazione, non soddisfacente; dopo altri vani
tentativi e lunghe discussioni, furono finalmente date varie dimostrazioni ineccepibili.
Alcune di esse differiscono per poco; notevole è quella di D. Hilbert, perché
indipendente dal postulato d’ARCHIMEDE.
D. HILBERT stabilisce infatti, senza ricorrere a questo postulato, ma con l’aiuto,
invece, del così detto teorema di PASCAL, un calcolo segmentario che conserva quasi
tutte le proprietà formali del calcolo numerico; dicendo indice di un triangolo il
prodotto dei due segmenti base e altezza , dimostra la indipendenza dell’indice dal
lato scelto come base, e la proprietà additiva dell’indice quando un triangolo si
scompone comunque in altri triangoli.
Definendo poi come indice di un poligono la somma degli indici dei triangoli nei quali
può venire scomposto, trova che esso è indipendente dalla scomposizione, e ne segue
che l’indice di un poligono è uguale alla somma degli indici di altri poligoni nei quali è
diviso. Ma gli indici sono segmenti, e per questi vale il principio analogo a quello di DE
ZOLT; il quale risulta perciò dimostrato per i poligoni.
42.Equivalenza e postulato di Archimede
1. Nell’ordinaria teoria dell’equivalenza non si riesce a dimostrare l’equiscomponibilità
di due parallelogrammi o triangoli di ugual base e uguale altezza senza ricorrere al
postulato di Archimede; si tratta qui di una reale impossibilità.
Se, infatti, A B C D è un parallelogrammo e si scompone in un numero qualunque n di
parti poligonali connesse la somma dei perimetri di queste è minore di n volte il
perimetro p del parallelogrammo; comunque si dispongano tali parti, una adiacente
all’altra e in modo che il vertice A appartenga alla nuova figura F così formata, la
distanza di un punto qualunque P di F da A sarà sempre minore di n p , cioè tutta la
figura F rimarrà nella regione intorno ad A i cui punti hanno da A distanza minore di un
multiplo di p.
Ma se il postulato di Archimede non vale, esistono anche punti fuori di questa regione
e si può costruire un parallelogrammo A B C’ D’ con la stessa base A B e la stessa
altezza di A B C D, ma con la base C’ D’ fuori della regione suddetta; allora è certo
che, scomponendo A B C D in poligoni, non si può, con questi, ricomporre A B C’ D’, e
cioè A B C D e A B C’ D’ non sono equivalenti.
2. D. Hilbert stabilisce una teoria dell’equivalenza dei poligoni indipendente dal
postulato di Archimede e da quello della continuità (integrità) considerando oltre
all’equiscomponibilità anche l’uguaglianza di area, che è un’equivalenza per differenza;
dicendosi
di
uguale
area
due
poligoni
quando
aggiungendo
equiscomponibili si possono avere poligoni equiscomponibili.
ad
essi
poligoni
Analisi dei comportamenti attesi:
− Strategia 1
Si traccia il disegno del rettangolo e si cerca di trovare figure
equivalenti all’interno di esso, equiscomponendolo.
Tali figure hanno un lato di 2 m e l’altro di 3m, dunque si prendono 2
strisce di 3 m di lunghezza.
− Strategia 2
Si calcola l’area del rettangolo che è di 12 m2.
Si divide l’area per la misura della larghezza della moquette e si
ottiene la lunghezza della striscia da acquistare, ovvero 6 m.
Tale valore viene diviso alternativamente per la lunghezza dei lati
della stanza e si sceglie come numero di strisce di guaina da ricavare
da quella acquistata il quoziente intero ottenuto dalle divisioni.
− Strategia 3
Si traccia il disegno del rettangolo e si cerca di trovare al suo
interno dei rettangoli con base di 2 m.
Trovati i rettangoli, si somma la lunghezza delle loro altezze,
ottenendo la lunghezza complessiva della striscia di guaina da
acquistare.
− Strategia 4
Sapendo che 4 è un multiplo di 2, si divide 4 per 2, ottenendo il
numero di strisce lunghe 3 m di guaina da acquistare.
− Strategia 5
Si traccia il disegno del rettangolo e si calcola l’area .
Si divide l’area per la misura della larghezza della guaina e si ottiene
la lunghezza della striscia da acquistare, ovvero 6 m.
Si inscrive il rettangolo di guaina ottenuto ( 2x6 m), all’interno di
quello raffigurante la stanza, sovrapponendo lungo il lato di 4 m.
Viene misurata la parte di guaina che fuoriesce dal perimetro della
stanza, la quale viene riportata nella superficie della stanza non
ricoperta.
− Strategia 6
Si traccia il disegno del rettangolo e si calcola l’area .
Si divide l’area per la misura della larghezza della guaina e si ottiene
la lunghezza della striscia da acquistare, ovvero 6 m.
Si inscrive il rettangolo di guaina ottenuto ( 2x6 m), all’interno di
quello raffigurante la stanza, sovrapponendo lungo il lato di 3 m.
Viene misurata la parte di guaina che fuoriesce dal perimetro della
stanza, la quale viene riportata, suddivisa in due parti, nella
superficie della stanza non ricoperta.
− Strategia 7
Si traccia il disegno del rettangolo e si dividono i lati più lunghi in 4
parti di 1 m ciascuna.
I lati più corti vengono divisi in 3 parti di 1 m ciascuno.
Osservando che lungo il lato minore, una striscia di guaina non è
sufficiente a coprire la stanza, mentre due sarebbero eccessive, si
sceglie di disporre i pezzi di guaina lungo il lato maggiore.
Si osserva che occorrono 2 strisce lunghe 3 m per ricoprire la
superficie della stanza.
TORNA