capitolo iii

47
CAPITOLO III
VARIABILI ALEATORIE
3.1 _ Definizione
Per numero aleatorio o variabile aleatoria si intende una funzione reale che fa
corrispondere ad ogni risultato di uno spazio campione Ω, probabilizzato, un numero reale;
è una grandezza della quale non si conosce a priori il valore che assumerà, ma solo il range
di valori che effettivamente potrà assumere (es. numero di anni prima che una
obbligazione venga estratta, tempo di durata di una lampadina).
Le più semplici variabili aleatorie sono quelle che assumono un numero discreto
finito di determinazioni, x1 < x2 <..< xn, che disporremo per comodità in ordine crescente,
ciascuna legata alla realizzazione di uno degli eventi E1, E2,.., En, formanti un sistema
completo di casi elementari possibili o partizione di Ω.
Nel caso di variabili aleatorie discrete infinite oppure continue infinite indicheremo
l'intervallo (a,b), aperto o chiuso, in cui i valori, indistinti uno dall’altro, possono cadere.
Noti i valori del numero aleatorio, devono essere assegnate le corrispondenti
funzioni di probabilità p1 < p2 <..< pn <…degli eventi associati, che nel caso in cui
costituiscono un insieme numerabile devono soddisfare la condizione di normalizzazione Σ
i
pi=1.
La distribuzione di probabilità di una variabile aleatoria viene quindi definita
dall’insieme delle determinazioni e dalle relative funzioni di probabilità. Se chiamiamo
spazio di probabilità il sistema completo di eventi incompatibili, una variabile casuale può
essere definita come una funzione avente per dominio uno spazio di probabilità e come
codominio un sottoinsieme di numeri reali.
La corrispondenza tra i valori assunti dalla variabile casuale e le rispettive
probabilità pi si chiama legge (funzione o distribuzione) di probabilità della X. In termini
fisici le legge ripartisce una massa unitaria in frammenti attribuibili ad ogni
determinazione. Geometricamente si esprime riportando in ordinata la quantità di massa
distribuita sui singoli valori disposti in ascissa. Nel caso discreto, la poligonale della
distribuzione da una visione ottica della legge di distribuzione; ciò non è possibile nel caso
continuo, in cui la probabilità che la variabile casuale assumi un ben determinato valore è
48
0.
Esempi
a) Considerate due urne, in una delle quali vi siano i numeri 5,6,7,8 e nell'altra i numeri
20,21,22. Si estragga un numero da ciascuna delle due urne e se ne faccia la somma. Gli eventi
possibili sono
E1=25, E2=26, E3=27, E4=28, E5=29, E6=30
con probabilità rispettive
p1=1/12, p2=2/12, p3=3/12, p4=3/12, p5=2/12, p6=1/12 tali che Σi pi =1
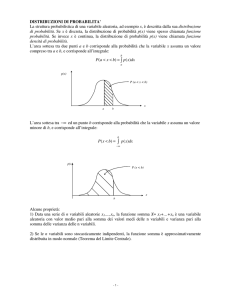
3.2 _ Funzione di distribuzione
La distribuzione di una variabile aleatoria X discreta oltre che sotto forma di
funzione di probabilità pi=pr(X=xi), può essere data anche attraverso la probabilità che
essa assuma un valore inferiore ad un prefissato valore x. Si ottiene la funzione di
distribuzione o di ripartizione F(x), o legge di probabilità cumulata, strumento che
permette di caratterizzare variabili casuali sia continue che discrete, fig. 3.1a-b. Si ha:
(3.1) F(x) = pr(-∝<X≤x) = pr(X≤x) =
∑
i / xi ≤x
pi ;
F(x) è una funzione sulle cui caratteristiche essenziali non ci soffermiamo, diciamo
solo che per una variabile casuale continua è anch’essa una funzione continua.
F(x1) =pr(X≤ x1)= p1
F(x2) =pr(X≤ x2)= p1+p2
La funzione di ripartizione, come la legge di distribuzione, definisce in modo quasi
completo il numero aleatorio e pertanto sarà lo strumento essenziale per lo studio di eventi.
3.3 _ Funzione di densità
La distribuzione di una variabile casuale X continua è definita dall’insieme non
numerabile dei valori che la variabile aleatoria può assumere e da una funzione che mostra
come X si distribuisce sul proprio campo di variazione. Tale funzione, oltre che nella
forma di funzione di ripartizione (3.1), può essere data anche sotto forma di funzione di
densità di probabilità.
(3.3) lim
Δx →0
F ( x + Δx) − F ( x)
d F ( x)
=
= F ' ( x ) , cioè una nuova funzione f (x )
dx
Δx
49
il cui valore numerico di f(x) non è una probabilità, ma esprime la velocità di
variazione della probabilità nel punto x. Se poi x è variabile su (a,b), f(x) è una funzione
che avrà le stesse prerogative della legge di distribuzione dei valori discreti.
La funzione f(x) dice come si addensa la probabilità: a parità di dx, pr(x≤X≤ x+dx) =
pr(x∈dx); essa è tanto più alta quanto più è grande il valore di f(x) in x e viceversa.
L’esistenza della f(x) deriva dalla condizione di derivabilità di F(x), mentre la sua
positività deriva dal fatto di essere derivata di una funzione non decrescente. Conoscendo
f(x), la funzione integrale permette di passare da f(x) ad F(x), attraverso una delle primitive
di f(x):
x
(3.5)
F(x) = pr(X<x) =
∫ f (t )dt
−∞
Avendo F(x) oscillazione pari a 1, l’equivalente della condizione di normalizzazione
+∞
per casi discreti, qui si traduce in
∫ f ( x)dx
= 1.
−∞
È da rilevare che f(x) dx è un elemento di probabilità ed assolve lo stesso ruolo
assolto dalle pi nelle variabili casuali discrete. Infatti la pr(α<X<β), in termini di funzione
β
di densità, è data da
∫ f ( x)dx
ed, in termini di funzione di ripartizione, da F(β)-F(α).
α
3.4 _ Caratteristiche di posizione
Il baricentro della distribuzione, che sinteticamente esprime l'andamento generale, è
detto valor atteso, ed è una media ponderata con le probabilità (se uguali si ha una media
aritmetica semplice), oppure con le frequenze relative hi/N dei valori xi, legati agli eventi
Ei, verificatisi hi volte, in N prove,
(3.6)
M(X) = μ = ∑ i xi pi =
∑x
i
i
hi
N
Tale numero esprime la previsione della media aritmetica dei valori che il numero
aleatorio assumerà in un numero N grande di prove. È importante dire un gran numero di
prove perché la frequenza è rappresentata dalla probabilità in un gran numero di prove. Il
valor medio per un numero aleatorio discreto e finito esiste sicuramente; per variabili
casuali discrete infinite si ha una serie che potrebbe non convergere.
Per moda di una variabile casuale discreta si intende il valore per cui è massima la
50
probabilità; per variabile casuale continue è quel valore di x per cui la funzione di densità
presenta un massimo; se presenta più massimi la distribuzione dicesi pluri-modale.
Per mediana si intende quel valore in cui la probabilità che la variabile casuale
assuma un valore inferiore ad esso è uguale alla probabilità che la variabile casuale assuma
un valore superiore, fig. 4.10
pr(X < x) = pr( X > x)
Come per una variabile statistica, per quantile qα di ordine α della distribuzione di
una variabile casuale X, si intende il più piccolo numero qα che soddisfa F(qα)≤α, se
discreta , oppure F(qα)=α, se continua.
+∞
(3.8bis)
M(X) =
∫ x f ( x)dx
−∞
Il valor medio ci dice solo il valore centrale del campo dei valori del numero
aleatorio, ma non ci dice nulla sulla grandezza del range. Dobbiamo vedere quindi se tutti i
valori sono addensati intorno al valor medio o se sono lontani da esso. Ad esempio, le due
variabili casuali X1 ed X2 in tabella
X1
p1
-100
.4
250
.6
X2
p2
50
.4
150
.6
hanno lo stesso valor medio e quindi la scelta sembrerebbe indifferente, ma non è
così perché la prima operazione prevede anche una perdita mentre la seconda prevede
comunque solo vincite: la prima è più rischiosa. Per avere una idea su questo aspetto
dobbiamo misurare gli scarti rispetto al valor medio.
3.5 _ Variabile casuale scarto
Costruiamo la variabile casuale scarto
Y=X-µ,
avente generica determinazione yi=xi-µ, per i=1,..n, corrispondente dell’evento Ei di
probabilità pi. Il suo valor medio risulta:
M(Y)= Σi yi pi = Σi (xi-µ) pi = µ- Σi µ pi=0
cioè somma algebrica degli scarti sempre nulla. Poiché la variabile aleatoria scarto
non fornisce nessuna informazione ulteriore, consideriamo la corrispondente variabile
casuale scarto assoluto |Y| = |X-µ|, che ha valor medio
51
M (|Y|) = Σ |yi pi| = Σ | (xi-µ) pi |.
Però il valore assoluto è difficile da trattare analiticamente poiché, presentando punti
angolosi, non è derivabile. Quindi al fine di avere gli scarti espressi positivamente, si eleva
Y a potenza pari, ottenendo analogamente:
Y²=(X-µ)² con il valore generico yi²=(xi-µ)².
Calcoliamo il suo valor medio, momento secondo rispetto a μ, detta varianza:
Var(Y)= Σi (xi-µ)² pi
Tale grandezza fornisce la dimensione dei quadrati degli scarti. Volendo tornare per
comodità alla stessa dimensione degli scarti, si utilizza lo scarto quadratico medio σ=√σ²;
Al crescere di σ, diminuisce l’addensamento dei valori rispetto a µ; è in realtà un
indicatore di dispersione, di densità, di concentrazione.
Valgono per la varianza le proprietà già viste per una variabile statistica e così pure
le due importanti relazioni:
m ( 2 ) = σ² = Σi (xi-µ)² pi = Σi x²i pi - 2 µ Σi xi pi + µ² Σi pi = M(X²)-2µ²+µ²=
= m( 2 ) - m(21) ,
Il momento secondo centrale è uguale al momento secondo rispetto all'origine meno
il valor medio.
3.7 _ Variabile casuale bernoulliana
E’ lo schema dell’esperimento bernoulliano che consiste in due prove legate ad un
evento elementare le cui realizzazioni nello spazio Ω(E,E) sono ripartite in un sistema
completo di eventi. Dato un evento E, indichiamo con |E| la variabile casuale indicatore di
E, che permette di collegare il calcolo delle probabilità classico che usa gli eventi a quello
moderno che usa le variabili casuali. Essa assume i valori
|E| =1 se si verifica l'evento E, con pr(E)= p
|E| =0 se si verifica E, con pr(E )= q=1-p
Il valor medio è M(|E|)=1p+0q=p, cioè la probabilità dell'evento e la varianza:
Var(|E|) = (0-p)²(1-p)+(1-p)²p = p²q+q²p=pq
3.8 _ Distribuzione uniforme discreta
È la distribuzione definita per valori aventi tutti la stessa frequenza relativa:
52
⎧1
per x = 1,2,...n
⎪
f(x) = ⎨ n
⎪⎩0 altrove
n 1
∑
i =1 n
=n
1
=1
n
f(x)
1/n
1 2 3
Fig. 3.4
k
n
La F(x), che per x < 1 vale 0 e per x>n vale 1, assume valore
x 1
F(x) = ∑
i =1 n
=
x
, per 1≤x≤n
n
1 n +1
=
2
n
k =1
n
M(X)= m(1) = ∑ k
n
Var(X) = m( 2 ) -µ² = ∑ k 2
k =1
1 ⎛ n +1⎞
1 n(n + 1)(2n + 1) ⎛ n + 1 ⎞
n2 −1
−⎜
=
−
=
⎟
⎜
⎟
6
12
n ⎝ 2 ⎠
n
⎝ 2 ⎠
2
2
3.9 _ Distribuzione uniforme continua
Considero un numero aleatorio X definito in un intervallo (a,b); poiché una scelta a
caso può cadere su qualsiasi valore x in esso incluso, non potremo dare la probabilità ad un
particolare numero che fosse diversa da quella daremmo ad altri; tutti i valori sono
equiprobabili e quindi il numero aleatorio ha densità di probabilità costante:
⎧k
f ( x) = ⎨
⎩0
per a ≤ x ≤ b
altrove
b
in cui k è una costante da trovare attraverso le condizioni k>0 ed
∫ k dx =1
a
Si ha k(b-a)=1 e quindi k = 1/(a-b)
La funzione F(x), per a≤ x≤b, assume valore
53
a
F(x) =
+∞
x−a
1
dt + ∫ 0dx =
b−a
b−a
b
a
x
∫ 0dx + ∫
−∞
Volendo calcolare la probabilità che x sia compreso in un intervallo di estremi (c,d)
compresi in (a,b), si ha:
pr(c<x<d) = F(d)-F(c) =
d
usando f(x) ottengo
d −a c−a d −c
−
=
b−a b−a b−a
d −c
1
∫ b − a dx = b − a
c
Per i momenti abbiamo:
µ = (a+b)/2
σ² = (b-a)2/12
Esempio
Considero ora un numero aleatorio X definito nell'intervallo (0,1); esso ha densità di
probabilità e funzione di ripartizione:
⎧0 per x ≤ 0
⎧0 per x ≤ 0
⎪
⎪
ed
F ( x) = ⎨ x per 0 < x < 1
f ( x) = ⎨1 per 0 < x < 1
⎪1 per x ≥ 1
⎪0 per x ≥ 1
⎩
⎩
F(x)
1
Δx
0.2
Fig. 3.7
0.7
Allora, volendo calcolare pr(0.2<x≤0.7), si ha F(.7)-F(.2)=.7-.2=.5 ed espresso
analiticamente F(x+Δx)-F(x)=f(x) Δx, ma essendo Δx=(0.7-0.2)=0.5, ne segue che f(x)=1.
3.10 _ La legge normale
La legge normale è una variabile causale continua avente funzione di densità
−
1
e
f(x)=
σ 2π
( x− μ )2
2σ 2
La distribuzione, completamente specificata dai parametri μ e σ, da calcolare con le
(3.8-9), è simmetrica intorno al punto medio M, coincidente con media, moda e mediana.
M=(μ,1 σ 2 π ), ed avente punti di flesso F aventi coordinate
F=( μ±σ, 1 σ 2 eπ ).
54
Se alziamo due perpendicolari dai punti che giacciono rispetto alla media ± 1σ, l'area
compresa fra esse e l'asse delle ascisse è pari al 68%; a ±2σ è il 95%; a ±3σ è il 99.7%.
3.11 _ La legge normale standardizzata
Per una variabile casuale normale X=N(μ,σ²), la trasformazione
Z=
X −μ
σ
produce una variabile casuale di legge normale avente media 0 e varianza 1, N(0,1),
detta normale standardizzata. In altre parole se si vuole conoscere la probabilità che X∈[µ-
σ,µ+σ], basta calcolare la probabilità che Z∈f([µ-σ,µ+σ])≡[-1,1]. Infatti z=[(µ-σ)-µ]/σ=-1
e poiché la z=f(x) è crescente, all'aumentare di x aumenteranno anche i valori di z: ad
esempio quando x raggiunge il valore µ+σ, z raggiunge il valore 1.
x
f(x)
μ−σ
μ
μ+σ
-1
0
+1
La variabile Z ha come funzione di densità
f (z) =
1
2π
z2
e 2
−
Definita la sua funzione di ripartizione con
Φ(z) = pr(Z≤z), abbiamo sussiste la relazione fondamentale:
F(x) = pr(X≤x) = pr(σZ+μ ≤ x) = pr(Z ≤ (x -μ)/σ) = pr( Z≤ z) = Φ(z)
Per cui fissata una probabilità α molto piccola, sono tabulati i quantili zα per cui:
pr(Z < zα ) = 1-α = Φ(zα), di conseguenza per:
pr(Z < -zα) = pr ( Z > zα ) = α = 1 - Φ(zα),
f(z)
Φ( zα)
fig. 3.5
μ=0
zα
55
Esempio
Una persona è sorteggiata da una popolazione di altezza media 177.80cm e scarto 5.08cm.
Calcolare la probabilità che la persona superi l’altezza di 182.88 cm?
pr(X>182.88) = pr ((x-177.8)/5.08 > ((182.88-177.8)/5.08) = pr (Z>1) ≈ 1-Φ(1) =.16.
La distribuzione normale è di notevole importanza nell’inferenza statistica, basta
citare il teorema che va sotto il nome di teorema del limite centrale
Sia {Sn} la somma di n variabili casuali indipendenti Xi aventi uguale legge di
probabilità o identicamente distribuite sopra lo stesso insieme finito di valori, tutte con
media M(Xi)=μ e scarto σ(Xi)=σ. Il teorema afferma che per n grande la distribuzione di
Sn è approssimativamente normale con media M(Sn)=nμ e scarto σ(Sn)=σ n , cioè:
{Sn} converge in legge verso N(nμ, σ n ).
Tale convergenza non riguardo solo Sn ma anche variabili aleatorie da essa derivate
come {Yn}=Sn/n, che avrà media M(Yn)=nμ/n=μ e varianza Var(Yn)=nσ2/n2=σ2/n, cioè:
{Yn} converge in legge verso N(μ, σ/ n ).
Per quest’ultima variabile aleatoria la legge dei grandi numeri è ancor più esplicita,
in quanto per n grande Yn tende a μ, con variabilità tendente a zero; ciò significa che quello
e che era un fenomeno aleatorio, diventa allora un fenomeno certo.
S − nμ
, essendo M(Zn)=0 e Var(Zn)=1,
La variabile casuale standardizzata Zn= n
σ n
converge in legge verso N(0, 1).
Ciò significa che la probabilità per cui a ≤ Sn≤ b è
pr(
a − nμ
σ n
≤
S n − nμ
σ n
≤
b − nμ
σ n
) ≈ Φ(
b − nμ
σ n
) - Φ(
a − nμ
σ n
)
3.14 _ Variabile casuale binomiale
Occupiamoci di calcolare la probabilità che su n prove, equiprobabili e indipendenti,
un certo evento abbia x successi, 0≤x≤n: è la somma di n bernoulliane
⎛n⎞
n!
pr(X=x) = Pn , x = ⎜⎜ ⎟⎟ p x q n− x =
p x q n− x
x! (n − x)!
⎝ x⎠
La loro somma soddisfa la condizione di normalizzazione:
∑
n
x =0
Pn , x = ( p + q) n = 1
∑
n
i =1
Ei
56
Considerato che gli Ei sono indipendenti, risulta:
M(X) = np, valore che risulta maggiore della varianza
Var(X)=Var( ∑in= 1 Ei ) =
∑
n
σ 2 ( Ei ) = npq
i =1