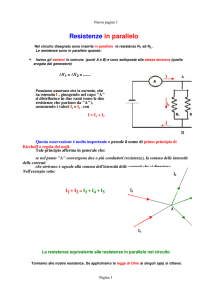
Resistenza equivalente.
Se un circuito complesso contiene un insieme di resistenze, è talvolta possibile sostituire tutte le resistenze (o
una parte di esse) con un’unica resistenza, detta resistenza equivalente Req, in modo tale che il comportamento
del resto del circuito rimanga immutato. Nei casi più semplici, quando le resistenze sono tutte in serie o tutte in
parallelo, le regole per calcolare la resistenza equivalente si ricavano dalle quattro affermazioni precedenti e
dalla prima legge di Ohm.
Resistenze in serie.
In laboratorio abbiamo constatato che
• in un circuito in serie, l'intensità della corrente elettrica è la stessa in tutti i punti del circuito
• in un circuito in serie, la d.d.p. esistente ai capi del generatore è uguale alla somma delle d.d.p. esistenti ai
capi dei singoli conduttori che compongono il circuito
In questo caso la resistenza equivalente è quella resistenza ai cui capi si ha la stessa d.d.p. che esiste, a parità
di corrente, ai capi delle resistenze in serie.
Dalla definizione di resistenza equivalente: ∆V AC = Req ⋅ i
Le due affermazioni corrispondono a
i = i1 = i2 (1) e ∆VAC = ∆VAB + ∆VBC (2)
Dalla legge di Ohm e tenendo conto della (1):
∆VAB = R1 ⋅ i1 = R1 ⋅ i e ∆VBC = R2 ⋅ i2 = R2 ⋅ i
∆V AC = ( R1 + R2 ) ⋅ i
Quindi, confrontando, Req = R1 + R2
usando la (2) e raccogliendo
Riassumendo: si dicono in serie due resistenze R1 e R2 disposte l’una di seguito all’altra in modo che la corrente
che le percorre sia la stessa. In un circuito con resistenze (2 o più) collegate in serie, la resistenza equivalente è
uguale alla somma delle singole resistenze.
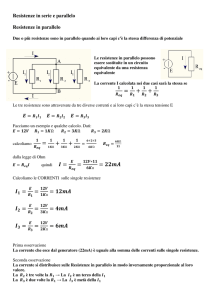
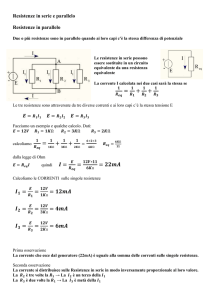
Resistenze in parallelo.
In laboratorio abbiamo constatato che
• in un circuito in parallelo, la corrente che attraversa il generatore è uguale alla somma delle correnti che
attraversano ciascuno dei rami in parallelo del circuito
• in un circuito in parallelo, la d.d.p. esistente ai capi del generatore è uguale a quella esistente ai capi di
ciascun conduttore presente nel circuito.
In questo caso la resistenza equivalente è quella resistenza che è attraversata dalla stessa corrente che fluisce
nel sistema delle resistenze in parallelo a parità di d.d.p. tra gli estremi.
La definizione di resistenza equivalente
∆V = Req ⋅ i si può scrivere i =
∆V
Req
Le due affermazioni corrispondono a
i = i1 + i2 (1) e ∆V = ∆V1 = ∆V2 (2)
Dalla legge di Ohm e tenendo conto di (2):
i1 =
∆V1 ∆V
∆V2 ∆V
=
e i2 =
=
R1
R1
R2
R2
usando la (1) e raccogliendo
i=
∆V ∆V
+
= ∆V
R1
R2
1
1
1
1
1
. Quindi, confrontando,
= +
⋅ +
Req R1 R2
R1 R2
Riassumendo: si dicono in parallelo due resistenze R1 e R2 disposte in modo che la d.d.p. ai loro capi sia
sempre la stessa. In un circuito con resistenze (2 o più) collegate in parallelo, il reciproco della resistenza
equivalente è uguale alla somma dei reciproci delle singole resistenze in parallelo.
Attenzione: sommando i reciproci delle resistenze si ottiene il reciproco della resistenza e non direttamente la
resistenza.
Analisi di circuiti elettrici.
Molti circuiti di uso comune, costituiti solo da generatori e resistenze, possono essere
ricondotti a circuiti elettrici elementari utilizzando le regole di composizione in serie e
in parallelo delle resistenze.
La figura a lato suggerisce il modo di procedere: si tratta di sostituire successivamente
a parti del circuito la resistenza equivalente di quella parte, finché tutta la rete viene
ricondotta ad una sola resistenza equivalente.
Per impadronirsi della tecnica l’unico modo è quello di risolvere qualche esercizio. La
difficoltà consiste nell’individuare le corrette parti da considerare, tenendo presente
che i termini serie e parallelo non si riferiscono a come sono disegnate, ma a come
sono collegate.
Quando la rete è stata tutta sostituta da un sola resistenza equivalente, si può
calcolare la corrente che esce dal generatore e successivamente le correnti e le d.d.p.
in ciascun resistore, applicando solo la prima legge di Ohm.
Non sempre è possibile analizzare un circuito elettrico formato da resistenze e
generatori con la tecnica descritta. È necessario allora ricorrere ad un metodo di
analisi più potente che fa uso delle leggi di Kirchhoff, usando le quali si scrive un
sistema di equazioni algebriche lineari la cui soluzione permette di determinare i valori
delle correnti e delle tensioni presenti nel circuito.
Esercizi.
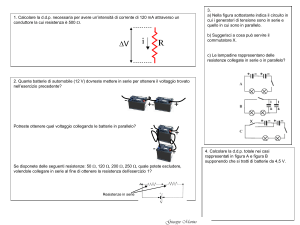
1. Quattro resistenze vengono collegate in parallelo. La prima misura 10 Ω, mentre le altre misurano,
rispettivamente, 20 Ω, 30 Ω e 40 Ω. Sapendo che la prima resistenza è attraversata da una corrente di
intensità 1 A, calcola le intensità delle correnti che circolano nelle altre tre resistenze e la tensione applicata.
2. Quattro resistenze vengono collegate in serie. La prima misura 10 Ω, mentre le altre misurano,
rispettivamente, 20 Ω, 30 Ω e 40 Ω. Sapendo che la prima resistenza è attraversata da una corrente di
intensità 1 A, calcola la d.d.p. ai capi di ciascuna altre tre resistenze e agli estremi della serie.
3. Con quattro resistenze, indicate rispettivamente con R1=20 Ω, R2=40 Ω, R3=100 Ω e R4=80 Ω si possono
realizzare diversi circuiti. Calcola:
• la resistenza equivalente del circuito nel caso che tutte le resistenze siano disposte in serie
• la resistenza equivalente nel caso che tutte siano disposte in parallelo
• la resistenza equivalente nel caso che il circuito sia formato da R1 e R2 in parallelo, poste poi in serie
con R3 e R4, anch’esse collegate tra loro in parallelo
• la resistenza equivalente nel caso che il circuito sia formato da R1 e R2 in serie, poste poi in parallelo
con R3 e R4, anch’esse collegate tra loro in serie
4. Due lampadine di 10 Ω e 5 Ω collegate in serie sono alimentate da una differenza di potenziale di 30V. Dopo
aver rappresentato schematicamente il circuito, calcola la resistenza equivalente delle due lampadine,
l’intensità di corrente che percorre il circuito e la caduta di tensione su ciascuna delle due lampadine.
5. Due resistenze da 10 Ω e da 30 Ω sono collegate in parallelo. Dopo aver rappresentato schematicamente il
circuito, calcola la resistenza equivalente. Se il sistema delle due resistenze in parallelo è alimentato da una
tensione di 12V, calcola l’intensità di corrente che attraversa ciascuna resistenza e l’intensità di corrente che
passa nel circuito.
6. Un circuito è costituito da due resistenze in serie, rispettivamente di 20 Ω e 10 Ω, collegate in parallelo con
una terza resistenza di 20 Ω. Calcola la resistenza equivalente del circuito. Se viene collegato ad un
generatore da 9 V, calcola la corrente in ciascuna delle resistenze.
7. Si vuole combinare un conduttore da 100 Ω con del filo di ferro ricavato da una matassa, di diametro 0,6 mm
in modo da ottenere una resistenza complessiva di 70 Ω. Che tipo di collegamento si deve fare? Quanto
deve valere la resistenza del filo di ferro? Quanti metri di filo occorrono?
8. Per ciascuna delle resistenze nei circuiti rappresentati in figura, calcola la corrente e la d.d.p. agli estremi.