Fluidi

1
Problema 1
Si calcoli il momento di inerzia di un disco omogeneo di massa M e raggio R rispetto ad un asse perpendicolare al disco
passante per il suo centro.
Il momento di inerzia vale:
I=
Z
r2 dm
R
Nel nostro caso particolare possiamo utilizzare lespressione del momento di inerzia di un anello di massa m e raggio r, che vale I = 12 mr2 . Dividiamo il disco in tanti anelli di raggio r e larghezza dr. Un tale anello
avrà una massa
r
O
M
2πrdr
πR2
e il momento di inerzia totale del disco sarà la somma (integrale) di tutti
gli anelli di larghezza infinitesima dr
dm =
I=
Z
r2 dm =
Z
r2
M
2πrdr = 2M
πR2
Z R
0
1
r3 dr = MR2
2
dr
2
Problema 2
Si calcoli il momento di inerzia di unasta rigida di massa M e lunghezza L, rispetto ad un asse perpendicolare allasta (a)
passante per il suo centro e (b) passante per un suo estremo
Calcoliamo il momento rispetto ad un estremo
I=
Z
dx
r2 dm
Dividiamo la nostra asta in tanti pezzetti lunghi dx a distanza x
dallestremo. La massa di un pezzetto di lunghezza dx sarà
x
0
L
M
dx
L
e il momento di inerzia totale del disco sarà la somma (integrale) di tutti i pezzetti
dm =
Z
Z L
Z
M
M L 2
1
dx =
x dx = ML2
L
L 0
3
0
Per calcolare il momento di inerzia rispetto al centro dovremo fare lo stesso integrale, ma partendo dal centro e andando verso
lestremo e questo integrale dovremo farlo due volte, da una parte e dallaltra dellasta.
Daltra parte, il singolo integrale è esattamente equivalemte a quello fatto nel caso precedente salvo sostituire L con L/2 e M
con M/2. In altre parole, abbiamo, due volte, il momento di inerzia rispetto ad un estremo di una sbarretta di lunghezza L/2
e massa M/2 Dunque otteniamo:
I=
r2 dm =
Ic = 2 ×
x2
1M
3 2
2
1
L
= ML2
2
12
Qesto risultato è in accordo con il teorema di Huigens-Stainer, che afferma....
3
Problema 3
Nel sistema raffigurato in figura un corpo pesante, di massa m1 = 4 kg, scivola lungo il piano inclinato liscio (α = 30o )
attaccato a una fune senza massa. La fune è avvolta attorno alla carrucola schematizzata come un cilindro pieno di raggio
R = 0.5 m e di massa M = 3 kg. L’altro estremo della fune è attaccato a un corpo pesante di massa m2 = 1 kg che scivola sul
tratto di piano orizzontale liscio. Il sistema è inizialmente fermo. Si lascia andare m1 che scende lungo il piano percorrendo
uno spazio L = 5 m, mettendo in rotazione la carrucola (la fune non slitta!) e trascinando m2 .
Calcolare: (a) la velocità delle due masse; (b) la loro accelerazione; (c) il momento delle forze che agiscono sulla carrucola.
m2
M,R
m1
30 gradi
Questo esercizio si può risolvere sia con le forze sia con la conservazione dellenergia. Consideriamo dapprima le equazioni
delle forze.
Siano T1 e T2 le tensioni sulle funi, diverse perchè cè la carrucola pesante in mezzo che accelera e le rende diverse. Posso
scrivere:
m1 a
=
m2 a
I ω̇
=
=
m1 g sin α − T1
T2
(T1 − T2 )R
ma ω̇ = a/R e il momento dinerzia di un cilindro omogeneo vale I = 1/2MR2 . Il sistema diventa allora:
= m1 g sin α − T1
= T2
m1 a
m2 a
1
Ma
2
= T1 − T2
Sommando le tre equazioni, le tensioni delle funi spariscono e si ottiene:
1
(m1 + m2 + M)a = m1 g sin α
2
⇒
a=
m1 g sin α
= 3.02 m/s2
m1 + m2 + 21 M
Il moto è un moto uniformemente accelerato e valgono le equazioni orarie
1 2
at
2
v(t) = at
x(t) =
Dalla prima ricavo il tempo che occorre per fare un tratto L, che poi sostituisco nella seconda.
v=
√
2aL = 5.49 m/s
Per ricavare il momento che agisce sulla carrucola si possono calcolare le tensioni T1 e T2 e usare la formula K = (T1 − T2 )R
oppure possiamo usare la formula
a
1
1
−
→
K = I ω̇ = MR2 = MRa = 2.26 N m
2
R 2
4
Consideriamo ora la conservazione dellenergia.
Il sistema, dapprima fermo, acquista unenergia cinetica a spese dellenergia potenziale gravitazioneale del blocco m1 che
diminuisce.
1
1
1
m1 gL sin α = m1 v2 + m2 v2 + Iω2
2
2
2
e considerando che I = 12 MR2 e che ω = v/R, si ottiene
1
1
m1 gL sin α = (m1 + m2 + M)v2
2
2
⇒
v=
s
2m1 gL sin α
= 5.49 m/s
m1 + m2 + 12 M
Come prima abbiamo un moto uniformemente accelerato. Il sistema da fermo acquista la velocità v dopo aver percorso lo
spazio L. Dalle equazioni del moto si ricava
v2
= 3.02 m/s2
2L
Se sostituiamo a v l’espressione trovata prima si ottiene esattamente lo stesso risultato che avevamo trovato con le forze.
Il momento delle forze applicate sul cilindro si trova esattamente come prima a apartire dall’accelerazione.
a=
5
Problema 4
Un’asta rigida di massa M = 4 kg e lunghezza l = 1.2 m può ruotare senza attrito sul piano orizzontale, attorno ad un asse
fisso passante per il suo centro (vedi figura). Un proiettile di massa m = 40 g e velocità v0 = 60 m/s urta l’asta in modo
totalmente anelastico in un punto che dista l/4 dal centro. La direzione del proiettile forma un angolo α = 20◦ rispetto ad un
asse perpendicolare all’asta.
Trovare (a) la velocità angolare dell’asta dopo l’urto, (b) l’energia cinetica persa nell’urto e (c) la forza (tangente al piano,
non il peso) cui è soggetto il perno che fa ruotare l’asta.
Si tratta di un urto completamente anelastico ed essendo l’asta vincolata nel suo centro, si
conserva il momento della quantità di moto, rispetto al centro dell’asta. Si consideri che
la direzione del proiettile non è ortogonale all’asta ed il braccio che devo considerare vale
l/4 cos 20◦ . Abbiamo cosı̀
v0
mv0 l/4 cos 20◦ = Iω + mv l/4
α
l/4
Ma d’altra parte v, velocità finale del proiettile, vale ω l/4 e sostituendo l’espressione del
momento di inerzia dell’asta otteniamo
mv0 cos 20◦
m 2
M
◦
l ω
⇒
ω=
+
= 1.40 s−1
mv0 l/4 cos 20 =
12 16
l(M/3 + m/4)
L’energia cinetica persa nell’urto vale
1
1
1
1
1
∆E = mv20 − Ml 2 ω2 − m(ω l/4)2 = mv20 −
2
24
2
2
2
M
m 2 2
+
l ω = 71.53 J
12 16
La forza tangenziale cui è soggetto il perno è la forza centrifuga del solo proiettile in quanto quella della sbarra si equilibra
esattamente essendo il perno nel centro
F = mω2 l/4 = 0.0235 N
6
Problema 5
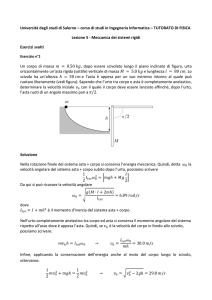
Una scala di massa m = 10 kg e lunghezza L è appoggiata con un estreamo A ad un muro e con lestremo B al suolo. Lattrito
in A è nullo ma è presente tra il pavimento e lestremo B. Se allequilibrio langolo tra la scala ed il muro vale 30o, calcolare:
(a) il coefficiente di attrito µs ; (b) langolo φ che la reazione vincolare in B forma con la verticale.
Le forze in gioco sono il peso, le due reazioni vincolari e la forza di attrito statico dullestremo della scala B. Su questo
estremo, componendo la pura reazione vincolare con la forza di attrito statico, abbiamo una reazione vincolare che forma un
angolo φ 6= 0 con la verticale.
Facciamo il momento delle forze rispetto al punto B e uguagliamolo a zero.
mg
L
sin 30◦ − TA · L cos 30◦ = 0
⇒
TA =
tan 30◦
2
2
Scriviamo poi la risultante delle forze (lungo x e lungo y) e uguagliamola a zero.
mg ·
−mg + TB cos φ =
TA − TB sin φ =
0
0
Da cui subito otteniamo:
11111111
00000000
00000000
11111111
00000000
11111111
00000000
11111111
00000000
11111111
00000000
11111111
00000000
11111111
00000000
11111111
00000000
11111111
00000000
11111111
00000000
11111111
00000000
11111111
00000000
11111111
A
mg
TA
1/2mg tan30◦ 1
tan φ =
=
= tan 30◦
mg
mg
2
e dunque
φ = tan−1 (1/2 tan 30◦ ) = 16.1◦
ϕ
B
Per quanto riguarda il coefficiente di attrito statico, la forza di attrito deve essere tale da non far cadere la scala e dunque:
Fa = µs TB cos φ > TB sin φ
cioè
µs > tan φ = 1/2 tan 30◦ = 0.289
7
Problema 6
Una pallina pesante di massa m = 80 g è lasciata cadere da un’altezza h = 60 cm e urta in modo completamente anelastico
un disco, rimanendovi attaccata. Il disco, di massa M = 0.4 kg e raggio R = 0.2 m, giace su un piano verticale e può ruotare
senza attrito intorno ad un asse passante per il centro. La pallina urta il disco, inizialmente fermo, nel punto A (vedi figura).
Trovare (a) la velocità angolare del disco quando la pallina si trova nella posizione B e (b) la quota massima h′ raggiunta
dalla pallina. (c) Da quale altezza deve cadere la pallina perchè dopo l’urto, ruotando sul disco, questa arrivi alla posizione
di massima altezza (punto D).
Il problema...
m
h
D
M,R
A
B
h’
8
Problema 7
Si calcoli il periodo delle piccole oscillazioni di un’asta rigida omogenea di massa m = 3 kg e lunga l = 1 m, vincolata al suo
estremo superiore (pendolo fisico)
Si tratta di valutare il moto di un corpo solido esteso dunque dobbiamo applicare la seconda
equazione cardinale della meccanica:
K = I ω̇
Il punto intorno al quale avviene il moto è l’estremo superiore dell’asta dove questa è incernierata. K è il momento delle forze applicate sull’asta, I è il momento di inerzia dell’asta rispetto
al suo estremo e ω̇ è l’accelerazione angolare a cui l’asta è sottoposta.
Poichè l’unica forza applicata sull’asta è il peso:
θ
mg
l
K = −mg sin θ
2
il segno meno è dovuto al fatto che per angoli positivi il momento tende a ruotare l’asta in senso orario (alla stessa conclusione
−
→ −
−
→ →
si arriva considerando che K = F × d ).
Il momento di inerzia di un’asta rispetto ad un’estremo vale:
1
I = ml 2
3
Sostituendo nell’equazione di sopra e considerando che ω̇ = θ̈ otteniamo
l
l
1 2
ml θ̈ = −mg sin θ ≈ − mgθ
3
2
2
Semplificando si ottiene
3g
θ=0
2l
Tale equazione è l’equazione di un moto oscillatorio con pulsazione e periodo
s
r
3g
2l
2π
ω=
T=
= 2π
= 1.64s
2l
ω
3g
θ̈ +
9
Problema 8
Un proiettile di massa m = 40 g e velocità v0 = 40 m/s urta in modo completamente anelastico (vi si conficca dentro) un’asta
rigida pesante (M = 1 kg, l = 1.2 m). L’urto avviene sul piano orizzontale, la velocità del proiettile forma un angolo α con
la normale all’asta (vedi figura) e l’asta può ruotare sul piano orizzontale intorno ad un perno passante per il suo centro.
Dopo l’urto l’asta acquista una velocità angolare ω = 6 rad/s e si ferma, a causa di una coppia frenante di attrito, in un tempo
∆t = 12 s.
Calcolare (a) l’angolo α; (b) l’energia persa nell’urto; (c) la coppia di attrito frenante
Il problema si risolve con la conservazione del momento
angolare
l
m v0 cos α = I ω
2
v0
1
1
I=
M l 2 + m l 2 = 0.2474 N · m
12
4
α = cos−1
m
ω
α
2Iω
= 32.9◦
mv0 l
L’energia persa vale
M
1
1
∆E = m v20 − I ω2 = 29.6 J
2
2
L’equazione che governa il moto della sbarra dopo l’urto
é l’equazione di un moto uniformemente decelerato con
decelerazione angolare τ/I, essendo τ la coppia frenante.
ω−
M
∆t = 0
I
⇒
M−
Iω
= 0.0672 N · m
∆t
10
Problema 9
Un disco di raggio R = 55 cm e massa M = 2.5 kg, inizialmente fermo, può ruotare liberamente attorno a un asse passante
per il suo centro. Un proiettile P di massa m = 500 g viaggia con velocita v0 = 11 m/s e urta nel bordo del disco (vedi figura)
con α = 40o. Dopo l’urto viene deviato come in figura con velocità v1 .
Sapendo che l’urto è elastico trovare: (a) la velocità angolare ω del disco dopo l’urto; (b) la velocità v1 di P dopo l’urto.
Se l’urto è invece completamente anelastico (il proiettile rimane conficcato nel disco) trovare (c) la velocità angolare ω2 del
disco dopo l’urto.
Il problema...
α
P
ω
α
R
11
Problema 10
Un’asta sottile rigida e pesante di lunghezza ℓ = 40 cm e massa M = 1 kg è sospesa a un estremo O attorno al quale può
ruotare senza attrito ed è inizialmente in equilibrio. Un corpo puntiforme di massa m viaggia orizzontalmente a velocitá V0 e
colpisce l’asta con urto elastico nel punto di mezzo. Dopo l’urto m rimane ferma mentre l’asta inizia a ruotare.
Determinare (a) il valore di m; (b) in queste condizioni (e cioé con m ferma) qual è il minimo valore di V0 necessario perchè
l’asta possa compiere un giro completo? (c) se l’urto fosse invece completamente anelastico quale sarebbe il periodo delle
piccole oscillazioni del pendolo risultante?
Il problema...
12
Problema 11
Un’asta di lunghezza L = 1 m e massa m = 3 kg è incernierata ad un’estremità mentre all’altra estremità è attaccata una massa
M = 8 kg (figura). Trovare il periodo delle piccole oscillazioni.
Anche in questo caso, si tratta di valutare il moto di un corpo solido esteso, dunque dobbiamo
applicare la seconda equazione cardinale della meccanica:
K = I ω̇
Il punto intorno al quale avviene il moto è l’estremo superiore dell’asta dove questa è incernierata. K è il momento delle forze applicate sull’asta, I è il momento di inerzia dell’asta rispetto
al suo estremo e ω̇ è l’accelerazione angolare a cui l’asta è sottoposta.
Il momento della forza peso (unica forza in gioco) sul sistema asta+palla sarà la somma dei
momenti della forza peso sull’asta e sul peso M
l
K = −mg sin θ − Mgl sin θ
2
Anche per valutare il momento di inerzia del sistema dovremo fare la somma dei due momenti
di inerzia, quello dell’asta più quello del peso.
1
I = ml 2 + Ml 2
3
Sostituendo nell’equazione di sopra e considerando che ω̇ = θ̈ otteniamo
1
l
l
( ml 2 + Ml 2 )θ̈ = −(mg + Mgl) sin θ ≈ −(mg + Mgl)θ
3
2
2
Semplificando si ottiene
θ̈ +
g( m2 + M)
θ=0
l( m3 + M)
Tale equazione è l’equazione di un moto oscillatorio con pulsazione e periodo
s
s
l( m3 + M)
g( m2 + M)
2π
ω=
T=
= 1.95s
= 2π
m
l( 3 + M)
ω
g( m2 + M)
Si può vedere che per M = 0 si ottiene il risultato dell’esercizio precedente, come deve essere.
m
θ
mg
M
Mg
13
Problema 12
Un cilindro pieno omogeneo, di massa M = 20 kg e raggio R = 15 cm, può ruotare intorno al suo asse posto orizzontalmente.
Due masse uguali (m = 3 kg) sono avvolte come in figura intorno al cilindro. Se il sistema parte da fermo, calcolare a) la
tensione di ciascuna corda, b) l’accelerazione di ciascuna massa e c) la velocità angolare del cilindro dopo che le masse sono
scese di un tratto h = 2 m.
Applichiamo la prima e la seconda equazione cardinale della meccanica rispettivamente ai due
pesi ed al cilindro.
Per il cilindro abbiamo
M,R
K = I ω̇
dove
1
I = MR2
2
K = 2T R
ω̇ =
a
R
m
Mettendo insieme si ottiene
1
a
2T R = MR2 ·
⇒
Ma = 4T
2
R
Applicando l’equazione F = ma a uno dei pesi (stessa equazione per entrambi), si ottiene
ma = mg − T
Abbiamo dunque un sistema di due equazioni e due incognite, da cui ricaviamo:
T=
mMg
= 18.4 N
4m + M
Ei
Ef
a=
4m
g = 3.68 m/s2
4m + M
= m1 gh
h 1
1
1
h
= m1 g + m2g + m1 v2 + m2 v2 + Iω2
2
2 2
2
2
La velocità angolare del cilindro si può calcolare dall’accelerazione, oppure applicando la conservazione dell’energia
2 2
MR2 2 (4m + M)R2 2
1
1
mR ω
+
2mgh = 2 mv2 + Iω2 = 2
ω =
ω
2
2
2
4
4
da cui si ricava:
2
ω=
R
r
2mgh
= 25.6 rad/s
4m + M
14
Problema 13
Una sbarretta di lunghezza l = 60 cm e massa M = 1 kg giace su un piano orizzontale, incernierata in un suo estremo
attorno al quale può ruotare senza attrito. Un proiettile di massa m = 300 g e velocità v0 = 30 m/s urta la sbarretta (in modo
perpendicolare) nel suo estremo libero e vi rimane conficcato. Calcolare la velocità angolare finale della sbarretta e l’energia
dissipata nell’urto.
M,l
v0
m
15
Problema 14
Uno spago è attaccato al soffitto da un lato, mentre l’altro lato è avvolto intorno ad un cilindro di massa M = 4 kg. Trascurando
ogni tipo di attrito, si calcoli l’accelerazione con cui il cilindro scende e la tensione a cui è soggetto lo spago.
→
−
→
Sul clindro agiscono due forze, la forza peso M −
g e la tensione della fune T . Inoltre il cilindro
avrà un moto uniformemente accelerato verso il basso ma avrà anche un moto di rotazione
intorno al proprio asse. Possiamo dinque scrivere:
Ma
=
I ω̇
=
Mg − T
TR
D’altra parte noi sappiamo che valgono le seguenti relazioni:
I
=
ω̇
=
11111111
00000000
00000000
11111111
M,R
1
MR2
2
a
R
Sostituendo nel sistema di sopra otteniamo
Ma
1
Ma
2
= Mg − T
= T
Questo sistema si risolve facilmente e si ottiene
a
=
T
=
2
g = 6.54 m/s2
3
1
Mg = 13.1 N
3
Come si vede, l’accelerazione del cilindro è inferiore all’accelerazione di gravità g, in quanto è presente la tensione della
fune, che mette in rotazione il cilindro.
16
Problema 15
Si consideri il sistema rappresentato in figua, in cui un pesetto m = 1 kg è attaccato ad un filo, la cui estremità opposta
è avvolta intorno ad un cilindro di massa M = 3 kg e raggio R = 20 cm. Se il sistema è inizialmente in quiete, calolare
a) l’acceleazione del pesetto, b) l’accelerazione del cilindro verso ilsuolo, c) l’accelerazione angolare del cilindro e d) la
tensione della fune.
Applichiamo le equazioni cardinali della meccanica per i due corpi, il peso ed il cilindro.
ma =
′
Ma =
I ω̇ =
mg − T
Mg − T
TR
dove a è l’accelerazione del peso, a′ è l’accelerazione del cilindro verso il basso e ω̇ è
l’accelerazione angolare del cilindro intorno al proprio asse.
D’altra parte sappiamo che valgono:
1
I = MR2
2
11111111
00000000
00000000
11111111
ω̇ = a + a′
e sostituendo queste relazioni nel sistema di partenza abbiamo
ma =
′
Ma =
M
(a + a′) =
2
mg − T
Mg − T
T
m
M,R
17
Problema 16
Un pendolo fisico è formato da un’asta sottile lunga L = 1 m e di massa M = 2 kg incernierata a un estremo. Il pendolo
viene spostato dalla verticale fino a un angolo α = −60o e lasciato andare. Quando passa per la verticale l’estremo libero urta
elasticamente una massa m = 1 kg che può scivolare senza attrito su un piano orizzontale. Calcolare:
(a) la velocità angolare del pendolo quando passa per la verticale; (b) la velocità della massa m dopo l’urto; (c) il momento
angolare del pendolo dopo l’urto.
Per trovare la velocità angolare dell’asta nella posizione verticale, prima dell’urto, applichiamo la conservazione dell’energia (potenziale
gravitazionale e cinetica).
1
1
L
Mg (1 − cosα) = Iω2 = ML2 ω2
2
2
6
⇒
ω=
r
M,L
α
3g(1 − cosα)
L
m
Consideriamo l’urto elastico, si conserva il momento della quantità di
moto e l’energia.
Iω
Iω2
= Iω f + mLv
1
= Iω2f + mv2
2
I(ω − ω f ) = mLv
⇒
⇒
I(ω − ω f )(ω + ω f ) = mv2
Dividendo la seconda per la prima otteniamo subito
ω + ωf =
v
L
⇒
ωf =
v
−ω
L
e sostituendo questo valore di ω f nella prima equazione e tenendo conto che I = 13 ML2 , abbiamo:
2MLω
v
= mLv
⇒
v=
I 2ω −
L
M + 3m
Il momento angolare finale dell’asta lo ricaviamo dall’equazione della conservazione del momento angolare:
1
L f = Iω f = Iω − mLv = ML2 ω − mLv
3
18
Problema 17
Un proiettile di massa m = 80 g viene sparato orizzontalmente con una velocità v0 = 80 m/s. Il proiettile urta in modo
totalmente anelastico un disco di massa M = 700 g e raggio R = 30 cm, libero di ruotare intorno ad un asse fisso verticale,
rimanendovi conficcato sul bordo (vedi figura 2). Se la distanza della direzione del proiettile dal centro del disco vale
d = 18 cm, calcolare:
(a) la velocità angolare del disco dopo l’urto; (b) l’energia dissipata; (c) la variazione di momento angolare del proiettile
rispetto al centro del disco.
m
ω
M,R
v0
d
Si conserva il momento angolare, dunque:
mv0 d = Iω + mR ω =
2
1
2
2
MR + mR ω
2
⇒
ω=
mv0 d
2
R ( 21 M + m)
Calcoliamo l’energia persa nell’urto facendo la differenza dell’energia iniziale e finale
1
1
∆Ec = mv20 − Iω2
2
2
dove I è il momento di inerzia, rispetto all’asse del disco, del disco più quello del proiettile, cioè:
1
I = MR2 + mR2
2
Sostituendo questa espressione di I e quella ottenuta per ω, otteniamo
"
#
md 2
1 2 1 2 1 2
∆Ec = mv0 − Iω = mv0 1 −
2
2
2
(m + 12 M)R2
La variazione di momento angolare del proiettile vale:
m
∆L = mv0 d − mωR = mv0 d 1 −
m + 21 M
2
!
19
Problema 18
Un’asta sottile omogenea di lunghezza L = 2 m e massa M = 200 kg poggia contro un muro verticale scabro (vedi figura).
Al suo estremo libero è attaccata una massa m = 100 kg, mentre una fune tiene il tutto in equilibrio con l’asta in posizione
orizzontale. Il coefficiente d’attrito statico fra asta e muro è µs e l’angolo fra la fune e la verticale vale θ = 45o .
Calcolare (a) la tensione T della fune; (b) l’angolo α fra la reazione vincolare del muro e la verticale; (c) il valore minimo di
µs per cui tutto questo è possibile.
Il sistema è in equilibrio e dunque la somma delle forze è uguale a zero come anche
la somma dei momenti delle forze (rispetto ad un qualsiasi punto). Ponendo uguali a
zero le componenti x e y delle forze abbiamo
F sin α − T cos45◦
=
0
F cos α + T sin 45◦ − (M + m)g =
0
45 o
Facciamo poi il momento delle forze rispetto al punto in cui l’asta poggia sul muro e
poniamolo eguale a zero
MgL/2 + mgL = sin 45◦ T L
T
α
M,L
Infine scriviamo quanto vale la forza di attrito statico sul muro
Fattr = F cos α = µs Fn = µs T cos 45◦
Abbiamo dunque quattro equazioni e quattro incognite. Dalla terza otteniamo subito
T=
(M + 2m)g
√
= 2773 N
2
Ricavando F dalla prima equazione e sostituendolo nelle altre possiamo facilmente risolvere il sistema e si ricava:
µs =
M
= 0.5
M + 2m
α = tan−1
M + 2m
= 63.4◦
M
m
20
Problema 19
Un’asta rigida di massa M = 4 kg e lunghezza l = 1.2 m può ruotare senza attrito nel piano verticale, attorno ad un suo
estremo fisso (vedi figura 2). L’asta viene spostata di α = −60◦ rispetto alla verticale e quindi, da ferma, lasciata libera di
ruotare. Quando passa per la verticale, l’asta urta un blocchetto di massa m = 2 kg in modo completamente anelastico.
Trovare la velocità angolare dell’asta (a) immediatamente prima dell’urto e (b) immediatamente dopo l’urto e (c) l’energia
persa nell’urto.
La velocità angolare dell’asta prima dell’urto la troviamo con la conservazione
dell’energia
M,l
1
1
L
Mg(1 − cosα) = Iω2 = ML2 ω2
2
2
6
α
da cui
ω=
r
m
3(1 − cosα)g
= 3.50 s−1
L
1111111111111
0000000000000
0000000000000
1111111111111
Durante l’urto si conserva il momento angolare, dunque, se ω′ è la velocità
angolare dopo l’urto abbiamo
Iω = Itot ω′
dove
Itot = I + mL2 e
1
I = ML2
3
Svolgendo si ottiene
M
ω = 1.40 s−1
M + 3m
L’energia che si perde nell’urto è la differenza delle energie cinetiche prime e dopo l’urto
ω′ =
1
1
2
∆E = Iω2 − Itot ω′
2
2
e sostituendovi dentro le espressioni dei momenti di inerzia I e Itot e di ω′ si ottiene
M
1
2 2
= 7.06 Joule
∆E = ML ω 1 −
6
M + 3m
21
Problema 20
Due masse (m1 = 15 kg e m2 = 10 kg) sono tenute sospese da una carrucola (M = 3 kg e R = 10 cm). La fune mette in
rotazione la carrucola. Le masse partono da ferme, distanziate di h = 3 m con m1 più in alto. Determinare la velocità delle
due masse quando si incrociano.
Il modo più semplice di risolvere questo problema è utilizzando la conservazione dell’energia.
Prendiamo lo zero dell’energia potenziale del campo gravitazionale alla quota del blocchetto 2
e scriviamo l’energia all’inizio, quando vengono lasciati, e al momento dell’incrocio (fine)
Ei
Ef
= m1 gh
h 1
1
1
h
= m1 g + m2g + m1 v2 + m2 v2 + Iω2
2
2 2
2
2
11111
00000
00000
11111
mgy
m1
Uguagliamo le due energie (non ci sono attriti) e consideriamo che valgono:
1
I = MR2
2
v
ω=
R
h
0 m2
Otteniamo:
h 1
M
m1 gh = (m1 + m2 )g + (m1 + m2 + )v2
2 2
2
Da questa è immediato ricavare v che vale:
s
gh(m1 − m2 )
v=
= 2.35 m/s
m1 + m2 + M2
Si noti che se m1 = m2 la velocità è nulla, cioè, come ci si aspetta, se le due masse sono uguali, il sistema è in equilibrio e
non si muove.
22
Problema 21
Un disco di raggio R = 50 cm e massa M = 2 kg ruota con velocità angolare ω = 3.4 rad/s (vedi figura). Un proiettile P di
massa m = 100 g e velocità v0 = 10 m/s si conficca nel bordo del disco (h = R/2). (a) Si determini la velocit‘a angolare ω1
del disco dopo lurto; (b) se sul disco agisce una coppia frenante di momento K = 0.10 Nm, quanti giri ci vorranno perchè il
disco torni alla velocità angolare iniziale?
Si tratta di un urto completamente anelastico in cui si conserva solo il momento
angolare e possiamo scrivere
mv0 h + Iω0 = mvR + Iω1v = ω1 R
e sostituendo v = ω1 R e I = (1/2)MR2 , con pochi passaggi possiamo ricavare
ω1 =
mv0 h + Iω0 2mv0 h + MR2 ω0 2
=
R = 4 rad/s
mR + I
(2m + M)
V0
ω
m
h
M,R
Il disco dunque aumenta la sua velocità angolare in seguito all’urto del proiettile, che gli dà una spinta nella stessa direzione in cui ruotava. Se ora applichiamo al disco una coppia costante, in senso
contrario alla sua rotazione, questo subisce una decelerazione angolare costante in base alla seconda equazione cardinale
della meccanica
K
I
L’equazione oraria dell’angolo θ e della velocità angolare ω saranno allora
I ω̇ = K
⇒
ω̇ =
K
K 2
t
ω(t) = ω1 − t
2I
I
e se vogliamo sapere quanti giri ha fatto il disco prima di tornare alla velocità ω0 , dobbiamo passare per il tempo che questo
ci impiega. Sia tale tempo t ∗
θ(t) = ω1 t −
I(ω1 − ω0 )
K ∗
t = ω0
⇒
t∗ =
= 1.5 sec
I
K
Sostituendo tale espressione di t ∗ nell’equazione di θ(t) otteniamo
ω1 − ω0
ω1 − ω0
MR2 2
Kt ∗
=I
ω1 −
=
(ω1 − ω20 ) = 5.5 rad = 0.875 giri
θ(t ∗ ) = t ∗ ω1 −
2I
K
2
4K
ω(t ∗ ) = ω1 −
avendo sostituito l’espressione del momento di inerzia di un disco I = 21 MR2 .
23
Problema 22
Un’asta priva di massa è tenuta in equilibrio come in figura ed alla sua estremità è appesa una massa M = 2 kg. Si calcoli
quanto vale la tensione T sulla fune se α = 25o e β = 65o .
Un tale problema si risolve ponendo la risultante delle forze uguale a zero e ponendo il
momento delle forze (rispetto ad un qualsiasi punto) uguale a zero.
Le forze in gioco sono:
• la forza peso del blocco, applicata sull’estremo dell’asta e diretta verso il basso
• la tensione della fune T , anch’essa applicata sull’estremo dell’asta e diretta lungo
la fune
α
• la reazione del muro sull’asta.
Scegliamo ora come punto rispetto a cui fare i momenti delle forze il punto in cui è
attaccata la fune ed il peso. Se γ è l’angolo che la reazione forma con l’asta, il peso e
la tensione T non contribuiscono e abbiamo
RL sin γ = 0
γ=0
⇒
cioè la reazione del piano è lungo l’asta.
A questo punto possiamo passare a considerare le componenti delle forze per
uguagliarle a zero
0 =
R sin β − T sin α
0 =
T cos α + R cosβ − Mg
⇒
R=
β
sin α
T
sin β
m
e sostituendo l’espressione di R trovata nella seconda equazione otteniamo
T cos α+T
sin α cos β
= Mg
sin β
⇒
T=
Mg sin β
Mg sin β
=
= Mg sin β = 17.8 N
cos α sin β + sin α cos β sin(α + β)
avendo considerato che α + β = 90o .
Che la reazione del muro sull’asta sia lungo l’asta non dipende dagli angoli α e β ma dal fatto che le due funi, quella che
sorregge l’asta e quella che sorregge il peso, sono attaccate nello stesso punto e dal fatto che la nostra asta non ha peso.
Allo stesso risultato si arriva uguagliando a zero la somma dei momenti rispetto al punto in cui l’asta è incernierata al muro.
In questo caso non devo conoscere nè il modulo della reazione R nè la sua direzione e ricavo subito
T L = MgL sin β
⇒
T = Mg sin β
e volendo conoscere solo La tensione T questo è sicuramente il modo più diretto.
24
Problema 23
Un’asta rigida di massa M = 2 kg e di lunghezza L = 80 cm è incernierata ad un estremo intorno al quale può ruotare
senza attrito in un piano verticale (figura 2). La sbarretta, inizialmente nella sua posizione di riposo verticale, viene urtata
elasticamente nel suo estremo libero da un blocchetto di massa m = 0.8 kg che viaggia ad una velocità v = 1.6 m/s.
Calcolare (a) la velocità dell’estremo mobile dell’asta immediatamente dopo l’urto (b) la velocità del blocchetto dopo l’urto
e (c) l’angolo massimo che l’asta forma con la verticale.
Si conserva sia il momento angolare che l’energia e possiamo scrivere
mv0 l = mvl + Iω
mv20 = mv2 + Iω2
Questo sistema può essere scritto nella forma:
Iω = ml(v0 − v)
Iω2 = m(v0 − v)(v0 + v)
e dividendo la seconda per la prima otteniamo subito
α
m
v
M,L
v0 + v
l
Se ora sostituiamo questo valore di ω nella prima equazione (quella lineare, relativa alla conservazione del momento angolare)
otteniamo
ω=
I
v0 + v
= ml(v0 − v)
l
⇒
v=
ml − I/l
3m − M
v0 =
v0 = 0.145 m/s
ml + I/l
3m + M
Come si vede, il fatto che il blocchetto continui ad andare aventi o rimbalzi indietro dipende unicamente dalle masse in gioco.
La velovità dell’estremo mobile dell’asta dopo l’urto vale
6m
v0 = 2.18 m/s
3m + M
Per calcolare l’angolo massimo raggiunto dall’asta applichiamo la conservazione dell’energia (cinetica e potenziale gravitazionale)
lω2
l
1 2
= 29.5o
Iω = Mg (1 cos θ)
⇒
θ = cos−1 1 −
2
2
3g
V = ωl = v0 + v =
avendo usato l’espressione del momento di inerzia dell’asta rispetto ad un estremo I = 13 Ml 3 .
25
Problema 24
Un’asta rigida ed omogenea di massa M = 8 kg e lunghezza L = 1.6 m è incernierata su un muro e può ruotare su un piano
verticale perpendicolare al muro stesso. Una molla di costante elastica k e lunghezza a riposo nulla collega l’estremo libero
dell’asta al soffitto (vedi figura). Quando l’asta si trova in posizione orizontale e la molla forma un angolo retto con il soffitto
il sistema è in equilibrio. Ad un certo istante si attacca una massa m = 10 kg all’estremo libero dell’asta e l’asta ruota verso
il basso.
Calcolare (a) la costante elastica k della molla; (b) l’energia cinetica T del sistema e (c) il momento delle forze K quando
l’asta passa per la posizione verticale.
Calcoliamo la costante elastica della molla usando la condizione di equilibrio iniziale. In particolare imponiamo
che il momento delle forze, rispetto al punto in cui è incernierata l’asta, sia nullo (la condizione che siano nulle
le forze non ci aiutano più di tanto in quanto aggiungono
due equazioni ma aggiungono anche due nuove incognite relative alle componenti della reazione della cerniera
sull’asta). Abbiamo allora:
Mg
L
⇒
k=
= 24.5 N/m
2
2L
Per calcolare l’energia cinetica quando l’asta passa per
la posizione verticale dobbiamo usare la conservazione
dell’energia.
kL2 = Mg
L
1
1
Mg +mgL+ kL2 = T + k5L2
2
2
2
⇒
L
L
1111111111
0000000000
00000000000
11111111111
0000000000
1111111111
00000000000
0000000000 11111111111
1111111111
00000000000
11111111111
0000000000
1111111111
00000000000
0000000000 11111111111
1111111111
00000000000
11111111111
0000000000
1111111111
00000000000
0000000000 11111111111
1111111111
00000000000
11111111111
L
L
k
M,L
M
= 94.1 J
T = gL m −
2
m
Si noti che, per un valore m < M/2, la sbarra non riesce ad arrivare alla posizione verticale perchè la massa attaccata non è
sufficentemente pesante.
Il momento delle forze quando l’asta è verticale è semplicemente il momento della forza della molla in quanto il momento
della forza peso (sia dell’asta che della massa attaccata) è nullo essendo il braccio nullo. Abbiamo dunque
√
L
MgL
· L = kL2 =
= 62.8 N · m
K = k 5L2 · √
2
2
5L
26
Problema 25
Una piattaforma circolare, di massa M = 300 kg e raggio R = 8 m, può ruotare senza attrito intorno ad un asse verticale
passante per il centro. La piattaforma inizialmente è ferma. Un uomo (m = 80 kg) si trova sul bordo della piattaforma
anch’egli in quiete. Ad un certo istante l’uomo comincia a correre lungo il bordo della piattaforma, di moto uniformemente
accelerato (rispetto alla piattaforma) e compie un giro completo della piattaforma in un tempo ∆t = 20 s.
Calcolare (a) l’accelerazione angolare α della piattaforma e (b) il momento K delle forze agenti su di essa mentre l’uomo sta
correndo. Calcolare infine (c) il lavoro L fatto dall’uomo nel compiere questo giro.
Il sistema piattaforma+uomo è isolato e dunque si conserva il momento angolare totale del sistema. Essendo tutto fermo
all’inizio, possiamo scrivere
Iω1 + mR2ω2 = 0
dove con ω1 e ω2 si sono rispettivamente indicate le velocità angolari della piattaforma e dell’uomo, rispetto al suolo.
Derivando quest’equazione troviamo la relazione tra le accelerazioni angolari.
2m
α2
M
avendo sostituito l’espressione del momento di inerzia della piattaforma in termini della sua massa e del raggio.
Noi conosciamo però l’accelerazione dell’uomo rispetto alla piattaforma che, se indicata con α, vale
Iα1 + mR2 α2 = 0
α1 = −
⇒
α = α1 − α2
avendo assunto il senso di rotazione positivo per la piattaforma e negativo per l’uomo. Poichè, girando, ci ritroviamo allo
stesso posto dopo un tempo ∆t, possiamo scrivere
4π
1
α ∆t 2 = 2π
⇒
α= 2
2
∆t
Abbiamo allora tree equazioni e tre incognite e possiamo trovare α2
α1 =
8πm
α
=−
= 0.0109 rad/s
(M
+
2m)∆t 2
)
(1 + 2m
M
Per calcolare il momento delle forze che agisce sulla piattaforma, si può usare la seconda equazione cardinale della meccanica.
4πmMR2
1
= 104.9 N · m
K = Iα1 = MR2 α1 =
2
(M + 2m)∆t 2
Infine il lavoro fatto dall’uomo quando ha fatto un giro rispetto alla piattaforma è semplicemente l’energia cinetica di tutto il
sistema.
1
1
1
1
L = Iω21 = mR2 ω22 = I(α1 ∆t)2 + mR2 (α2 ∆t)2
2
2
2
2
e calcolando anche α2 e sostituendo si trova il valore numerico. Se si sostituiscono le espresiioni analitiche di α1 e α2 si
ottiene il risultato
2mM
L=
M + 2m
2πR
∆t
2
= 659 J
27
Problema 26
Una giostra può essere schematizzata come un disco pesante omogeneo di massa M = 300 kg e raggio R = 5 m, che può
ruotare sul piano orizzontale intorno ad un asse verticale passante per il suo centro. La giostra, inizialmente ferma, viene
messa in rotazione applicando un momento costante K = 100 N·m. Si calcoli (a) la velocità angolare della giostra, dopo
che ha compiuto sei giri. A questo punto si smette di applicare il momento K e un uomo (m = 80 kg) sale sulla giostra
posizionandosi sul bordo di essa. Si calcoli (b) la velocità della giostra dopo che l’uomo è salito e (c) l’energia cinetica persa
al momento della salita dell’uomo.
Bisogna applicare la seconda equazione cardinale della meccanica.
2K
1
⇒
α=
K = MR2 α
2
MR2
Sapendo l’accelerazione angolare, calcolare la velocità angolare dopo aver compiuto sei giri è un problema di cinematica.
r
√
1 2
2 Kθ
θ = αt
ω = αt
⇒
ω = 2θα =
= 1.42 rad/s
2
R M
Quando l’uomo sale sulla giostra il momento angolare del sistema si conserva e dunque possiamo scrivere.
M
1
1
2
2
2
⇒
ω=
MR ω0 =
MR + mR ω
ω0 = 0.624 rad/s
2
2
M + 2m
K = Iα
⇒
avendo indicato con ω0 la velocità angolare prima che l’uomo salisse sulla giostra.
L’energia che si perde è data dalla differenza delle energie cinetiche.
1
1
1
1
1
∆E = Iω20 − (I + mR2 )ω2 = MR2 ω20 −
MR2 + mR2 ω2
2
2
4
4
2
28
Problema 27
Un’asta omogenea di massa M = 1 kg e lunghezza L = 1 m può ruotare senza attrito in un piano verticale intorno al punto
A fissato in un suo estremo (vedi figura). All’altro estremo B è fissata una massa puntiforme di massa M = 1 kg. L’asta,
inizialmente ferma in posizione orizzontale, urta un corpo (in modo elastico), anch’esso di massa M, fermo nel punto C su
un piano scabro di coefficiente di attrito dinamico µd = 0.2.
Calcolare (a) la velocità angolare dell’asta prima dell’urto e (b) dopo l’urto, e (c) la distanza d percorsa da M prima di
fermarsi.
L’esercizio può essere diviso in due parti, prima la discesa verso la
verticale e poi l’urto elastico.
m
B
m,L
A
m
29
Problema 28
Si calcoli l’accelerazione di un cilindro (R = 15 cm e M = 2 kg) che rotola su un piano inclinato di un’angolo α = 20◦ . Si
ripeta il calcolo se a rotolare è un anello o una sfera piena (sempre dello stesso raggio e dello stesso peso.
Applichiamo le equazioni cardinali della meccanica
M,R
α
30
Problema 29
Si calcoli il periodo delle piccole oscillazioni di una ruota (R = 15 cm e M = 2 kg) assimilabile ad un cilindro, attaccata ad
una molla di costante elastica k = 300 N/m (vedi figura).
0110
0
1
11111111110
000000000
M,R
k
31
Problema 30
Un’asta rigida pesante di lunghezza l = 0.8 m e massa M = 3 kg è incernierata in un suo estremo ad un punto fisso e può
ruotare intorno ad esso su un piano verticale (vedi figura). Un proiettile di massa m = 1.2 kg è sparato orizzontalmente con
una velocità v = 10 m/s e urta l’asta nel suo punto di mezzo. Dopo l’urto il proiettile esce dall’asta senza deviare con velocità
v/2.
Calcolare: (a) la velocità angolare dell’asta dopo l’urto; (b) l’energia dissipata nell’urto; (c) la velocità minima che dovrebbe
avere il proiettile per far compiere all’asta un giro completo.
Si tratta di un urto parzialmente anelastico in cui si perde un po di energia
ma i due corpi non sono attaccati alla fine.
m
v
v/2
M,l
32
Problema 31
Un recipiente cavo di volume V = 200 litri e massa m = 50 kg viene riempito d’acqua e lasciato sprofondare nel mare
(ρl = 1000 kg/m3). Si può considerare il volume della cavità uguale al volume esterno. Il recipiente scende nell’acqua con
velocità costante a causa della resistenza dell’acqua rappresentata da una forza costante di modulo Fv .
Trovare: (a) il valore di Fv . Una volta sul fondo il recipiente viene svuotato e lasciato risalire. Trovare:
(b) l’accelerazione del corpo se il modulo della forza resistente non cambia; (c) la sua velocità limite ascensionale se il
modulo della forza resistente dipende invece dalla velocità secondo la formula Fv = k v con k = 150 Ns/m.
Quando la cavità è piena d’acqua, l’equazione del moto è
ma = mg + ρH2 OV g − ρH2 OV g − Fv
essendo la forza di Archimende uguale e opposta al peso dell’acqua contenuta (il volume dell’involucro è supposto trascurabile). Il recipiente scende a velocità costante, dunque a = 0 e otteniamo:
Fv = mg
Quando il recipiente viene vuotato, abbiamo la forza di Archimede, la forza frenante Fv e il peso del solo involucro, dunque
l’equazione diventa:
ρH2 OV
−2 g
ma = ρH2 OV g − Fv − mg
⇒
a=
m
Nel caso che la forza resistente si proporzionale alla velocità Fv = k v, abbiamo:
ma = ρH2 OV g − mg − kv
La velocità cresce finchè il termine frenante non diventa uguale alle altre forze che muovono il recipiente e si raggiunge un
equilibrio in cui l’accelerazione è nulla
ma = ρH2 OV g − mg − kv∞ = 0
da cui otteniamo
v∞ =
(ρH2 OV − m)g
k
33
Problema 32
Due cilindri di uguale forma (altezza h = 0.6 m e raggio R = 0.2 m) sono attaccati ai due estremi di una fune che passa
intorno ad una carrucola priva di massa ed attrito (figura 2). I due cilindri hanno rispettivamente densità ρ1 = 1200 kg/m3
e ρ2 = 1800 kg/m3 e sono parzialmente immersi in acqua. Il sistema è in equilibrio quando il cilindro 1 è emerso per una
lunghezza x mentre il cilindro 2 è immerso per la stessa lunghezza x. Calcolare (a) la lunghezza x e (b) la tensione della fune.
Se ad un certo istante si rimuove improvvisamente l’acqua, si calcoli (c) l’accelerazione a del sistema.
Per entrambi i corpi, uguagliamo a zero la somma delle forze. Indicando con T la
tensione della fune e V il volume dei cilindri, abbiamo
ρ1V g − T − ρH2 OV g(1 − x/h) = 0
ρ2V g − T − ρH2 OV gx/h = 0
Se risolviamo nelle due incognite x e T otteniamo:
x
=
T
=
ρ2 − ρ1
h
= 0.48 m
(1 +
2
ρH2 O
(ρ2 − ρH2 O x/h)V g = 739.3 N
x
ρ1
Se non c’è più l’acqua non abbiamo più la spinta di Archimede e possiamo scrivere
le equazioni
ρ2
m1 a
m2 a
= T − m1 g
= m2 g − T
Sommando le due equazioni troviamo subito
a=
m2 − m1
ρ2 − ρ1
g=
g = 1.961 m/s2
m2 + m1
ρ2 + ρ1
x
34
Problema 33
Un pendolo fisico è formato da un’asta sottile lunga L = 1 m e di massa M = 2 kg incernierata a un estremo. Il pendolo
viene spostato dalla verticale fino a un angolo α = −60o e lasciato andare. Quando passa per la verticale l’estremo libero urta
elasticamente una massa m = 1 kg che può scivolare senza attrito su un piano orizzontale. Calcolare
(a) la velocità angolare del pendolo quando passa per la verticale; (b) la velocità della massa m dopo l’urto; (c) il momento
angolare del pendolo dopo l’urto.
Per trovare la velocità angolare dell’asta nella posizione verticale, prima dell’urto, applichiamo la conservazione dell’energia
(potenziale gravitazionale e cinetica).
r
1 2 1
3g(1 − cosα)
L
2 2
⇒
ω=
Mg (1 − cosα) = Iω = ML ω
2
2
6
L
Consideriamo l’urto elastico, si conserva il momento della quantità di moto e l’energia.
Iω
Iω2
= Iω f + mLv
1
= Iω2f + mv2
2
I(ω − ω f ) = mLv
⇒
⇒
I(ω − ω f )(ω + ω f ) = mv2
Dividendo la seconda per la prima otteniamo subito
ω + ωf =
v
L
⇒
ωf =
v
−ω
L
e sostituendo questo valore di ω f nella prima equazione e tenendo conto che I = 13 ML2 , abbiamo:
2MLω
v
= mLv
⇒
v=
I 2ω −
L
M + 3m
Il momento angolare finale dell’asta lo ricaviamo dall’equazione della conservazione del momento angolare:
1
L f = Iω f = Iω − mLv = ML2 ω − mLv
3
35
Problema 34
Un corpo di massa M = 10 kg e volume V = 5 litri è attaccato all’estremo di una fune ideale e di massa nulla avvolta su una
carrucola cilindrica di massa m = 8 kg e raggio R = 20 cm (vedi figura). Il tutto è immerso in acqua (ρ = 1000 kg/m3). Si
lascia andare da fermo la massa M.
Trovare: (a) l’accelerazione della massa M; (b) la tensione della fune; (c) la velocità angolare della carrucola dopo che la
massa è scesa di H = 1 m.
Dovendo calcolare l’accelerazione del sistema, applichiamo al peso ed alla carrucola pesante
rispettivamente la prima e la seconda equazione cardinale della meccanica
Ma
I ω̇
= Mg − ρH2 OV g − T
= TR
Sostituendo l’espressione del momento d’inerzia della carrucola (I = 12 mR2 ) e considerando
che ω̇ = Ra , otteniamo
Ma
=
ma =
(M − ρH2 OV )g − T
2T
Risolvendo otteniamo
m
M+
a = (M − ρH2 OV )g
2
⇒
a=
(M − ρH2 OV )g
M + m2
111
000
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
Dalla seconda equazione del sistema di sopra è immediato trovare T:
T=
(M − ρH2 OV )g
1 + 2M
m
La velocità dopo che la massa è scesa di H = 1 m, si trova facilmente con la conservazione dell’energia, considerando che
tra le forze c’è sia il peso che la forza di Archimede
1 2 1 2
Iω + Mv = (M − ρH2 OV )gH
2
2
Esplicitando il momento di inerzia e scrivendo v in termini di ω troviamo
1
m 2 2
M+
ω R = (M − ρH2 OV )gH
2
2
⇒
1
ω=
R
s
2(M − ρH2 OV )gH
M + m2
M
36
Problema 35
Un oscillatore armonico lungo l’asse x è formato da una massa attaccata a una molla di costante elastica k. Si misura la
velocità per due valori di elongazione della molla trovando per x1 = 11 cm v1 = −8 m/s e per x2 = 5 cm v2 = 10 m/s.
Calcolare
(a) il periodo di oscillazione. Se m = 100 g: (b) l’ampiezza di oscillazione; (c) il valore di x per cui l’energia cinetica e
potenziale sono uguali.
Non essendoci attrito, l’energia totale (potenziale della molla più energia cinetica) si conserva e possiamo scrivere:
1 2 1 2 1 2 1 2
kx + mv = kx + mv
2 1 2 1 2 2 2 2
Da questa dividendo per m otteniamo
k 2
k
k 2
x1 + v21 = x22 + v22
⇒
(x − x22 ) = v22 − v21
m
m
m 1
Considerando ora che ω = k/m e che T = 2π/ω possiamo scrivere
s
x21 − x22
2π
v22 − v21
2
⇒
T=
= 0.1026 s
= 2π
ω = 2
2
ω
x1 − x2
v22 − v21
Applichiamo la stessa conservazione anche al punto di elongazione massima della molla in cui il peso è fermo:
1 2 1 2 1 2
kx + mv = kA
2 1 2 1 2
A2 = x21 +
⇒
m 2
v
k 1
Ma noi sappiamo che
m x21 − x22
= 2
k
v2 − v21
e dunque
2
A =
x21 +
x21 − x22
v22 − v21
v21
2
A =
⇒
s
x21 +
x21 − x22
v22 − v21
v21 = 17.1 cm
Il valore di x per cui energia potenziale e cinetica sono uguali si ricava imponendo che l’energia potenziale sia la metà di
quella totale cioè
1 ∗2 1 2
kx = kA
2
4
⇒
A
x∗ = √ = 12.1 cm
2
37
Problema 36
Un blocchetto di massa m = 1.0 kg è collegato, tramite un filo inestensibile ed una carrucola priva di massa, ad un cilindro
di massa M = 4.0 kg e raggio R = 0.3 m (vedi figura). Il collegamento della fune al cilindro è tale che il cilindro può
ruotare senza attrito intorno al suo asse. Inoltre tra piano ed cilindro vi è attrito statico in modo che quest’ultimo rotola senza
strisciare. Il sistema, inizialmente fermo, ad un certo istante è lasciato libero di muoversi.
Calcolare (a) l’accelerazione del sistema dopo che il blocchetto è sceso di un tratto h = 3 m, (b) la tensione T cui è sottoposta
la fune e (c) la forza di attrito che agisce sul cilindro.
Il problema....
M,R
m
38
Problema 37
Una sbarretta rigida pesante di massa M = 4.0 kg e lunghezza L = 1.0 m è incernierata ad un suo estremo, attorno al quale
può ruotare senza attrito nel piano verticale. La sbarretta, che inizialmente forma un angolo α = 120o rispetto alla verticale
(vedi figura), è lasciata cadere e quando passa per la verticale urta in modo completamente anelastico un blocchetto di massa
m = 1.2 kg.
Calcolare (a) la velocità angolare della sbarretta poco prima di urtare il blocchetto, (b) la massima altezza raggiunta dall’estremo libero della sbarretta dopo l’urto e (c) l’energia persa nell’urto.
Il problema....
M,L
α
O
m
39
Problema 38
Una bidone di volume V2 e massa m = 120 kg è attaccato tramite una fune ad un pallone aerostatico riempito di Elio (ρHe =
0.18 kg/m3) di volume V1 = 80 m3 (massa del pallone trascurabile). Se pallone e bidone sono in aria (ρaria = 1.3 kg/m3)
si osserva che il sistema scende con accelerazione costante −a. Quando invece il pallone è in aria mentre il bidone è
completamente sommerso in acqua (vedi figura), il sistema sale con la stessa accelerazione a. Calcolare
(a) il volume del bidone V2 ; (b) l’accelerazione a e (c) quanta parte del bidone risulta immersa nell’acqua quando questo
galleggia sempre attaccato al pallone.
Il problema....
V1
a
a
m
V2
40
Problema 39
Una sferetta di volume V1 = 200 cm3 e densità ρ1 = 8 g/cm3 viene rivestita in polistirolo (ρ2 = 0.04 g/cm3) per renderla
galleggiante in acqua (ρa = 1 g/cm3 ) (si intenda che galleggia sotto il pelo dell’acqua, completamente immersa).
Calcolare: (a) il volume minimo possibile del rivestimento di polistirolo V2 ; (b) la massa totale del sistema; (c) la sua
accelerazione (verso l’alto o il basso) se invece che in acqua il tutto viene lasciato libero, completamente immerso in un
liquido di densità ρl = 0.7 g/cm3 .
41
Problema 40
Una massa M = 1 kg è fissata a un estremo di una fune inestensibile e di massa trascurabile avvolta su una carrucola cilindrica
di raggio R = 20 cm e massa Mc = 2 kg (vedi figura) azionata da un motore. Il sistema è inizialmente fermo. Il motore viene
avviato ponendo la carrucola in rotazione in senso antiorario con accelerazione angolare costante. Dopo un tempo T = 2 s la
massa M è salita di un’altezza h = 2 m mentre la carrucola ha acquistato una velocit‘a angolare ω. Si calcoli: (a) la velocit‘a
angolare della carrucola, (b) la tensione del filo e (c) il lavoro fatto dal motore.
42
Problema 41
Un recipiente cilindrico appoggiato al suolo è riempito di un liquido ideale sino ad unaltezza H = 1 m. Su una parete laterale
(vedi figura) sono praticati due fori di sezione trascurabile rispettivamente a quota h1 = 0.2 m e h2 = 0.4 m rispetto al pelo
libero. Supponendo che il livello H del liquido sia mantenuto costante calcolare: (a) quanto deve essere largo un recipiente
posto a terra in grado di raccogliere l’acqua prodotta da entrambi i getti e (b) le coordinate del punto di intersezione (x, y).
43
Problema 42
Un recipiente cavo di volume V = 2.40 litri e massa m si trova immerso in acqua (ρ0 = 1000 kg/m3). Si può considerare il
volume della cavità uguale al volume esterno. Se la cavità è vuota il recipiente sale a galla con accelerazione a. Se invece la
cavità viene riempita con un liquido di densità ρL = 1400 kg/m3 si trova che affonda con accelerazione −a.
Trovare: (a) la massa m del recipiente; (b) l’accelerazione a; (c) la frazione di volume fuori dall’acqua nel caso in cui il
recipiente è a galla vuoto.
44
Problema 43
Due blocchetti di uguale massa m = 4 kg sono collegati da una fune che scorre su una carrucola cilindrica di massa M = 6 kg
(vedi figura 3). Considerando che un piano è inclinato di 45◦ rispetto all’orizzontale, calcolare l’accelerazione del sistema (a)
se i piani sono lisci e (b) se è presente un attrito dinamico con µd = 0.1. Calcolare infine (c) l’accelerazione del sistema se sul
piano inclinato non c’è attrito ma il blocchetto di sinistra (blocchetto appeso in verticale) è immerso nell’acqua (si assuma
che abbia un volume V = 2 litri).
Scriviamo le equazioni cardinale del moto per i tre corpi (nell’ordine: il blocchetto appeso, il blocchetto sul piano inclinato e la
carrucola)
ma =
ma =
I ·ω =
m
⇒
1
Ma = T1 − T2
2
1111111111
0000000000
0000000000
1111111111
0000000000
1111111111
0000000000
1111111111
0000000000
1111111111
0000000000
1111111111
0000000000
1111111111
0000000000
1111111111
0000000000
1111111111
0000000000
1111111111
0000000000
1111111111
M,R
m
m
mg − T1
T2 − mg cosθ
(T1 − T2 )R
1111111111
0000000000
0000000000
1111111111
0000000000
1111111111
0000000000
1111111111
0000000000
1111111111
0000000000
1111111111
0000000000
1111111111
0000000000
1111111111
0000000000
1111111111
0000000000
1111111111
0000000000
1111111111
M,R
m,V
Sommando le tre equazioni si ottiene:
M
a 2m +
= mg(1−sinθ)
2
⇒
a=
mg(1 − sinθ)
= 1.044 m/s2
2m + M2
Se c’è l’attrito si procede allo stesso modo e comparirà la forza di attrito µd g cos θ nella seconda equazione del sistema.
Otterremo
a=
mg(1 − sinθ) − µd cos θ
= 0.792 m/s2
2m + M2
Se non c’è attrito ma il blocchetto verticale si trova nell’acqua, aggiungiamo alla prima equazione del sistema la forza di
Archimede ρH2 OV g con segno meno (opposta alla forza peso). Otteniamo
m(1 − sinθ) − ρH2 OV
M
= mg(1 − sinθ) − ρH2 OV g ⇒ a =
a 2m +
g = −0.738 m/s2
2
2m + M2
Essendo l’accelerazione venuta negativa, significa che il sistema ora si muove verso destra cioè il blocchetto verticale
(immerso nell’acqua) sale mentre quello sul piano scende.
45
Problema 44
Un tubo a U (vedi figura) di sezione S1 = 5.0 cm2 nel ramo sinistro e S2 = 3.0 cm2 nel ramo destro è riempito di mercurio
(ρHg = 13.6 g/cm3). Si versano nel ramo destro 100 g di acqua (ρH2O = 1.0 g/cm3) per cui il dislivello del mercurio tra i
due vasi vale ∆h.
Trovare: (a) l’altezza H della colonna d’acqua; (b) il valore di ∆h; (c) la variazione di pressione nel punto più basso del tubo
dopo l’introduzione dell’acqua.
Il problema...
S1
S2
S1
S2
H
∆h
Hg
H2O
Hg
*
*
46
Problema 45
Un corpo cuneiforme di massa m = 1.2 kg e volume V = 1.55 litri è lasciato cadere da un’altezza h = 2 m in acqua (vedi
figura).
(a) Nell’ipotesi che non vi sia attrito, calcolare la massima profondità H raggiunta dall’oggetto.
Assumendo invece che in acqua agisca una forza di attrito costante Fa = −1.5 N (sempre contararia al senso di moto),
calcolare (b) la massima profondità raggiunta H ′ e (c) la velocità v con cui l’oggetto ritorna al pelo dell’acqua.
Il problema si puó risolvere sia con la conservazione dell’energia sia con le forze. Utilizziamo il primo che é piú semplice e
prendiamo lo stato iniziale al culmine, prima di cadere, e lo stato finale quando si ferma al punto piú basso in acqua. L’energia
potenziale gravitazionale va in lavoro della forza di Archimede.
mg(h + H) = ρH2 OV gH
⇒
H=
mh
= 6.86 m
ρH2 OV − m
Allo stesso modo se c’è la forza di attrito posso scrivere (cioè
aggiungo il lavoro fatto dalla forza di attrito)
mg(h+H ′) = ρH2 OV gH ′ +Fa H ′
H′ =
⇒
m,V
h
mgh
= 4.77 m
ρH2 OV g − mg + Fa
Per calcolare la velocitá con cui torna su il corpo, applichiamo
sempre la conservazione dell’energia ma prendendo come punto
finale quello in cui il corpo torna al pelo dell’acqua. In questo
caso il lavoro della Archimede ha segno opposto quando scende
e quando sale e dunque si elide.
1
mgh = 2FaH + mv2
2
′
⇒
v=
r
2gh −
4Fa H ′
= 3.92 m/s
m
H
47
Problema 46
Un corpo omogeneo di volume V = 6.0 litri, galleggia in una vasca riempita di LST (ρLST = 2.85 g/cm3) in modo tale che
il volume immerso V2 è uguale al volume emerso V1 (vedi figura 1). Calcolare (a) la densità del corpo. Successivamente si
aggiunge nella vasca dell’acqua, in modo che questa copra completamente il corpo (l’acqua si deposita sopra il liquido LST).
Calcolare (b) quanto vale il volume del corpo immerso nel mercurio. Se in tali condizioni si vuole immergere completamente
il corpo nel mercurio, (c) quale forza bisogna applicare, dall’alto verso il basso, al corpo?
H2 O V’1
H2 O
V1
F
V’2
V2
Hg
Il problema...
Hg
Hg
48
Problema 47
Un’asta sottile pesante lunga L = 1.80 m di massa M = 1.95 kg ruota senza attrito attorno a un asse orizzontale passante per
un estremo. L’asta è solidale con un tamburo di raggio R = 0.40 m e massa nulla centrato sullo stesso asse. Sul tamburo è
avvolta una funicella di massa trascurabile attaccata a un estremo a un peso di massa m (vedi figura 2).
(a) Il sistema è tenuto inizialmente fermo con l’asta verticale rivolta verso il basso. A t = 0 si lascia andare il peso e si
osserva che l’asta ruota di un angolo α = 70o fino ad arrestarsi per poi tornare indietro. Calcolare il valore della massa m.
(b) Calcolare l’angolo β che corrisponde alla posizione di equilibrio stabile del sistema per un valore di m = 2.50 kg. Se per
questo stesso valore di m il sistema viene lasciato libero come in (a) calcolare la velocità V con cui scende il peso quando il
sistema passa per la posizione di equilibrio (angolo β).
Il problema...
R
θ
M,L
m