Soluzione-Meccanica

Politecnico di Bari - Facoltà di Ingegneria
Corso di Laurea in Ingegneria Gestionale
Corso di Fisica Generale (A e B), esame del 9 Luglio 2009
PROBLEMA 1
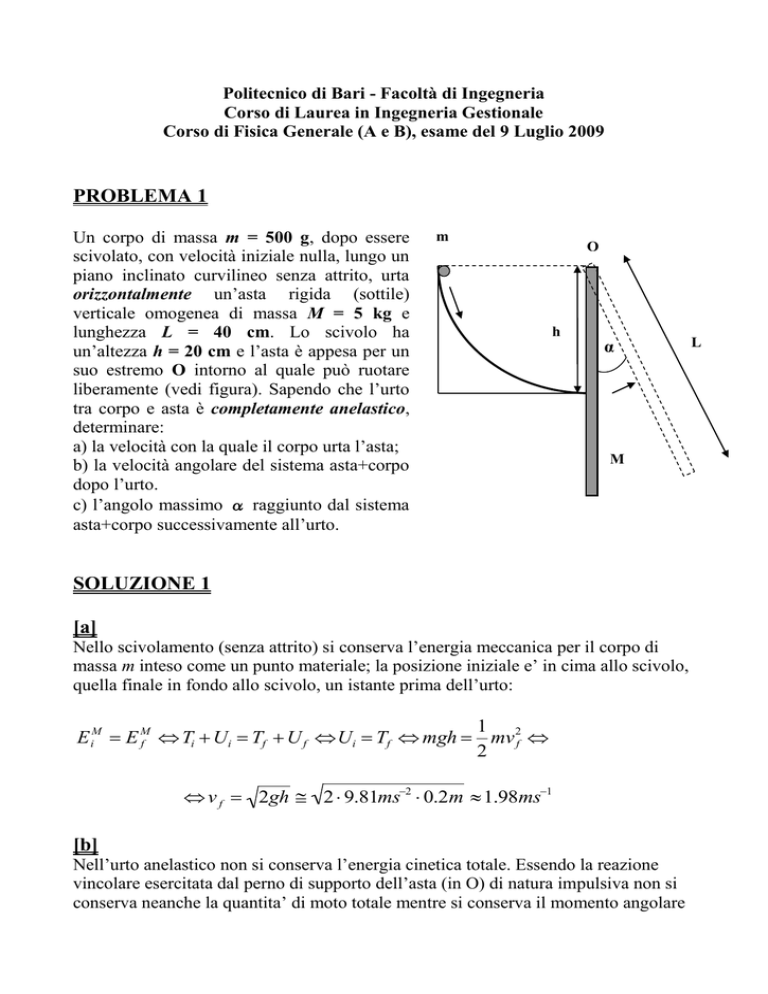
Un corpo di massa m = 500 g, dopo essere
scivolato, con velocità iniziale nulla, lungo un
piano inclinato curvilineo senza attrito, urta
orizzontalmente un’asta rigida (sottile)
verticale omogenea di massa M = 5 kg e
lunghezza L = 40 cm. Lo scivolo ha
un’altezza h = 20 cm e l’asta è appesa per un
suo estremo O intorno al quale può ruotare
liberamente (vedi figura). Sapendo che l’urto
tra corpo e asta è completamente anelastico,
determinare:
a) la velocità con la quale il corpo urta l’asta;
b) la velocità angolare del sistema asta+corpo
dopo l’urto.
c) l’angolo massimo αraggiunto dal sistema
asta+corpo successivamente all’urto.
m
O
h
α
M
SOLUZIONE 1
[a]
Nello scivolamento (senza attrito) si conserva l’energia meccanica per il corpo di
massa m inteso come un punto materiale; la posizione iniziale e’ in cima allo scivolo,
quella finale in fondo allo scivolo, un istante prima dell’urto:
1
E iM  E Mf  Ti  Ui  Tf  U f Ui  Tf  mgh  mv 2f 
2
 v f  2gh  2  9.81ms2  0.2m 1.98ms1

[b]
Nell’urto anelastico non si conserva l’energia cinetica totale. Essendo la reazione
 esercitata dal perno di supporto dell’asta (in O) di natura impulsiva non si
vincolare
conserva neanche la quantita’ di moto totale mentre si conserva il momento angolare
L
totale del sistema (asta+corpo) riferito al polo O (rispetto al quale il momento della
reazione vincolare e’ nullo):
LTOT
 LTOT
 mvi h  IoTOT  f
i
f
dove v i  v f  1.98ms1 e’ la velocita’ del corpo prima dell’urto che e’ proprio la
velocita’ finale del corpo in fondo allo scivolo.

 Il momento d’inerzia totale (dopo l’urto) e’:
I
TOT
o
 mh  I
2
ASTA
o

1
L 2 
L 2
1
ASTA
2
2
 mh  ICM  M   mh   ML  M   mh 2  ML2
2  
2  
3

12
2
Possiamo ricavare la velocita’ angolare del sistema dopo l’urto:

mvi h
3mvi h
3mvi
3 0.5Kg1.98ms1
f 



 0.69 rad s
2
2
1
(3m  4 M)h (1.5  20)Kg 0.2m
mh 2  ML2 3mh  4 Mh
3
[c]
Non essendovi attrito sul perno durante la rotazione l’energia meccanica totale si
conserva. La posizione iniziale e’ quella subito dopo l’urto mentre quella finale viene
raggiunta quando il sistema si ferma (all’angolo massimo). L’energia potenziale
iniziale viene posta nulla alla quota del baricentro G subito dopo l’urto (con l’asta
praticamente ancora in posizione verticale); ovviamente G coincide con il centro
dell’asta dove si e’ conficcato il corpo.

1
E iM  E Mf  Ti  Ui  Tf  U f  Ti  U f  IoTOT i2  (m  M)gh(1 cos )
2
dove  i   f  0.69rads1 e’ la velocita’ angolare iniziale del sistema che e’ proprio la
velocita’ angolare subito dopo l’urto. Sviluppando la relazione si ricava  :






1 
4
43
 mh 2  Mh 2 i2  (m  M)gh(1 cos )  mh 2 i2 11mgh(1 cos )


2 
3
6
43 h i2
0.2m  0.692 s2
 (1 cos )  
 0.65 
 0.0063
66 g
9.81ms2
 cos 1 0.0063    arccos(0.00369)    6.48o