Esercizi sul calcolo di derivate

L2.mat, punto di formazione per Matematica e Fisica
Esercizi sul calcolo di derivate
(funzioni composte con le inverse delle funzioni circolari)
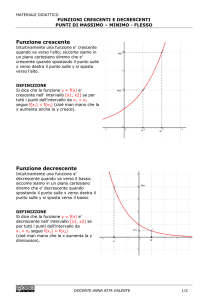
E1) f  x   arcsen  2 x 
 1 1
La funzione è definita nell’insieme D    ;  ed è continua e limitata.
 2 2
Il codominio della funzione è l’intervallo [-1;1].
La funzione derivata prima è
f ' x  
 1 1
ed il suo dominio è l’intervallo aperto   ;  .
 2 2
1  4 x2
2
La funzione f è strettamente crescente e assume il valore minimo nel
primo estremo del dominio x=-1/2 e il valore massimo nel secondo
estremo x=1/2. Risulta

 1
1 
min  f      , Max  f    .
2
 2
2 2
E2) f  x   arcsen
Figura 1- Diagramma della funzione
f  x   arcsen  2 x 
 x
La funzione è definita nell’intervallo D  0;1 ed è limitata. Il codominio della funzione è
 
Codom  f   0; 
 2
La funzione derivata prima è
f ' x  
1
1
1


1  x 2 x 2 x 1  x 
che è definita nell’intervallo aperto 0;1 .
La funzione derivata prima nell’intervallo di definizione è positiva, quindi
la funzione f è strettamente crescente in tutto il suo dominio e
conseguentemente assume il minimo assoluto nel punto x=0, che vale 0,
e il massimo assoluto nel punto x=1 che vale /2.
Si osservi che f  0    , f 1   .
'

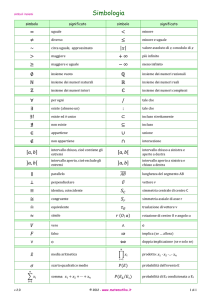
Figura 2- Diagramma della funzione
f  x   arcsen
 x
'

1
E3) f  x   arccos  
 x
Il dominio di definizione della funzione è D  ; 1  1;  .
Luigi Lecci: www.matematicaescuola.it
Pagina 1
L2.mat, punto di formazione per Matematica e Fisica
La funzione è limitata, perché lo è la funzione arccos(y), e il suo codominio è un sottoinsieme dell’intervallo
[-1;1].
La funzione derivata prima è
f ' x  
1
x
x2  1
…
E4) f  x   ln  arcsen  x  
La funzione è definita nell’intervallo D  0;1 , è limitata superiormente ma non inferiormente.
…
Es5) f  x   arc t g  ln  x  
La funzione è definita nell’intervallo D  0;  .
f ' x  
La funzione derivata prima è
1
1
 e il suo dominio di definizione coincide con quello
2
1  ln  x  x
della funzione f. La funzione derivata prima è strettamente positiva ed essendo la funzione f definita in un
intervallo quest’ultima sarà strettamente crescente in tutto il dominio.
…
Estremi della funzione
ma risulta Inf  f   

2
, Sup  f  

2
.
…
6) f  x   2arcsen

1  x2

La funzione è definita nell’intervallo [-1;1], è continua e quindi per il teorema di Weierstrass è limitata e
ammette minimo e massimo.
Derivabilità
1
… f ' x   2 
1

1 x
2

2

1
2 1  x2
  2 x  
2 x
x 1  x2
,…
Altre caratteristiche
…
Luigi Lecci: www.matematicaescuola.it
Pagina 2