Forze centrali 1
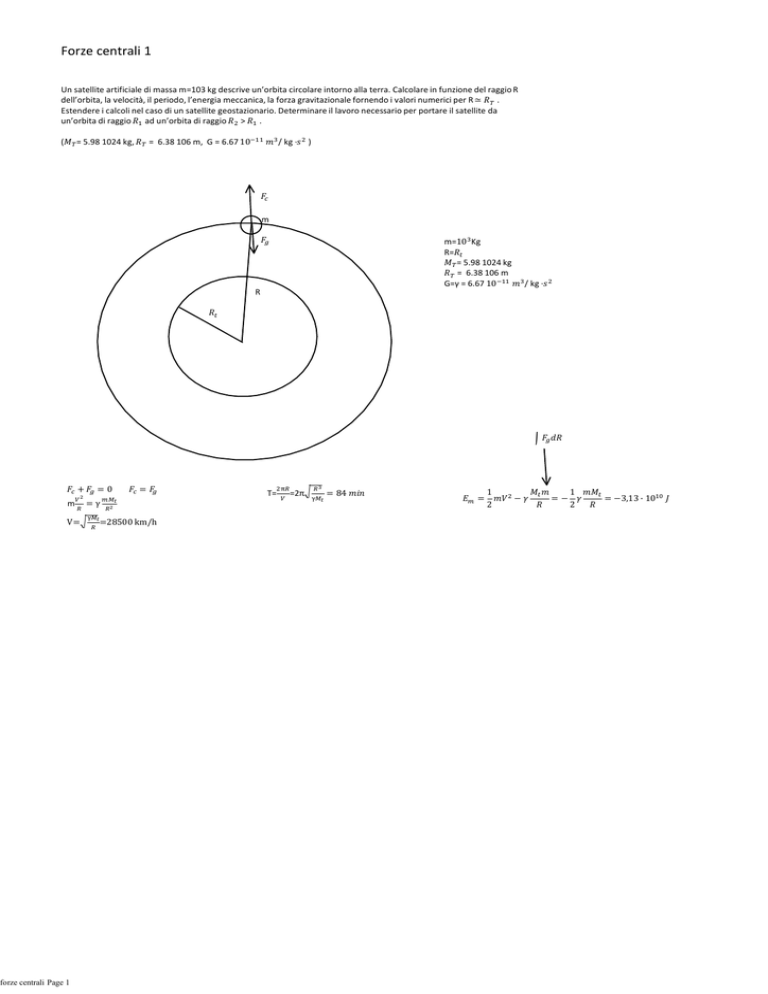
Un satellite artificiale di massa m=103 kg descrive un’orbita circolare intorno alla terra. Calcolare in funzione del raggio R
dell’orbita, la velocità, il periodo, l’energia meccanica, la forza gravitazionale fornendo i valori numerici per R ≃
.
Estendere i calcoli nel caso di un satellite geostazionario. Determinare il lavoro necessario per portare il satellite da
un’orbita di raggio ad un’orbita di raggio > .
(
= 5.98 1024 kg,
= 6.38 106 m, G = 6.67
/ kg ∙
)
m
m=
R=
Kg
= 5.98 1024 kg
= 6.38 106 m
G=γ = 6.67
R
T=
m
V=
forze centrali Page 1
=28500 km/h
=2π
/ kg ∙
Forze centrali 2
Un satellite di massa m descrive un’orbita circolare intorno ad un pianeta di massa M . Determinare l’energia totale in
funzione di m, M e L . Si ponga l’energia potenziale gravitazionale all’infinito uguale a zero.
forze centrali Page 2
m
L
=0
M
Forze centrali 3
Si vuole collocare un satellite artificiale su un’orbita circolare a quota H dalla superficie terrestre. Tenendo in
considerazione la rotazione della terra, si calcoli il minimo lavoro necessario a tale scopo in queste due situazioni:
a. il satellite è lanciato dal polo
b. il satellite è lanciato dall’equatore.
Si esprimano i risultati in funzione della massa m del satellite, della quota H , della costante di gravitazione universale G,
della massa della terra M , del suo raggio
e del periodo di rotazione T .
forze centrali Page 3
h
Forze centrali 4
Calcolare la velocità di fuga di un corpo di massa m dalla terra
forze centrali Page 4
Forze centrali 5
Due particelle, caricate rispettivamente con carica 3q e q , sono poste a una mutua distanza 3d . Considerato il punto P
rappresentato in figura, si calcoli:
forze centrali Page 5
Forze centrali 6
Uno spettrometro di massa è uno strumento che consente di misurare la massa di particelle quali atomi o molecole.
Supponiamo di fornire calore alla sostanza esaminare. In questo modo è possibile ottenere degli ioni che hanno una arica
q . Gli ioni percorrono una zona in cui sono presenti un campo elettrico E ed un campo magnetico
ortogonali
tra loro scelti in modo da tale da non deflettere gli ioni che possiedono una velocità prestabilita s v . Gli ioni che possiedono
questa velocità entrano quindi in una seconda zona in cui è presente un campo magnetico
che li deflette fino a quando
essi colpiscono una lastra fotografica. Supponendo di scegliere = 2 m/s dimensionare correttamente lo spettrometro e
calcolare a quale distanza D gli ioni colpiranno la lastra fotografica se la loro massa è
m=
e
0.5 T
forze centrali Page 6
Forze centrali 7
Un circuito a forma di triangolo rettangolo isoscele di lato 2a percorso da una corrente I è immerso
all’interno di un campo magnetico B uniforme, perpendicolare al piano del circuito e verso uscente
dal foglio. Si calcoli la forza risultante (modulo, direzione e verso) agente sul circuito.
forze centrali Page 7
Forze centrali 8
Un elettrone parte da fermo da un punto distanza d =1 cm da due protoni che distano d fra loro
ed arriva nel loro unto medio Q. Sapendo che la massa dell’elettrone è
calcolare la velocità dell’elettrone in Q.
forze centrali Page 8