IL NUMERO <<e>>
Consideriamo la successione
Al crescere di n i valori tendono ad un valore limite , un numero irrazionale (con infinite
cifre decimali , non periodico) e trascendente (non è soluzione di alcuna equazione
algebrica a coefficienti interi) al quale il matematico svizzero Eulero(1707-1783)
assegnò il nome <<e>>, forse l’iniziale del suo nome, ma più probabilmente come
simbolo di <<esponenziale>>, in quanto è stato scelto come base privilegiata per le
funzioni esponenziali e logaritmiche ( in Analisi Matematica la suddetta scelta rende
più semplici le operazioni di derivazione e di integrazione delle funzioni esponenziali e
logaritmiche).
I logaritmi in base e sono detti infatti logaritmi neperiani, o anche naturali, per una ragione che
vedremo in seguito.
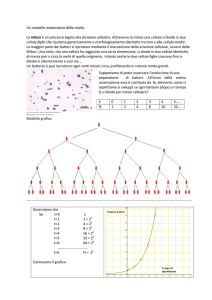
I calcoli riportati a lato , eseguiti con EXCEL, danno un’idea del valore numerico di
<<e>>, che si dimostra essere compreso fra 2 e 3.
I suoi valori approssimati, fino alla dodicesima cifra decimale, possono essere
memorizzati utilizzando una filastrocca, tra quelle premiate in un concorso bandito dalla
rivista Sapere nel 1935
Qui potete trovare un file compresso con il primo milione di cifre
GENESI DEL NUMERO e ( un esempio)
Immaginiamo che una Banca riesca a convincere Paperon de’ Paperoni ad
investire una bella somma , pari ad 1 milione di dollari , promettendogli di
raddoppiare ogni anno il suo capitale iniziale C
Alla fine di ogni anno, quale sarebbe il valore della somma disponibile?
Indichiamo con M, quello che si chiama il montante, cioè il capitale iniziale
più gli interessi, maturati in un
certo numero n di anni.
In tabella:
Immaginiamo ora che il il fortunato papero ponga un’ulteriore condizione al Direttore di Banca:
il calcolo del Montante deve avvenire avvenga non più ogni anno,
mese per mese..
Qual è la ragione di una simile richiesta?
Se nella prima ipotesi il tasso annuale era del 100%, ovvero uguale ad 1, il tasso mensile dovrà
uguale a 1/12. Pertanto dopo un mese il Montante sarà dopo due mesi (1 + 1/12)2. Dopo un anno
non avremmo quindi 2 milioni di dollari , come avevamo visto all’inizio, ma
1 000 000 x (1 + 1/12)12 = 2 620 000
La determinazione della formula generale, per quella che si chiama capitalizzazione composta e
che si trova su qualsiasi libro di Matematica Finanziaria, può aiutarci a capire meglio il problema.
Se calcoliamo il montante per un anno, al tasso annuo i (nel nostro esempio 100%) avremo
M = C(1 + i)
Se calcoliamo invece il montante per un anno, ma suddividendo l’anno in due semestri e aggiungiamo
l’interesse, calcolato dopo i primi sei mesi, al capitale iniziale, avremo il nuovo montante
M = C(1 + i/2)2
Infatti, per sei mesi, il tasso di interesse è i/2 (nell’esempio precedente sarebbe il 50%). Quindi il montante
dopo i primi sei mesi è
M1 = C + C i/2 = C ( 1 + i/2)
Ed è su questo che dobbiamo calcolare il nuovo montante per i successivi sei mesi:
M = M1 + M1 i/2 = M1 (1 + i/2) = C ( 1 + i/2)(1 + i/2) = C(1 + i/2)2
Allo stesso modo, se suddividiamo l’anno in tre parti, e l’interesse maturato nel primo quadrimestre lo
aggiungiamo al capitale iniziale per produrre, insieme con esso, il nuovo interesse nel quadrimestre
successivo e seguiamo ancora questo procedimento per l’ultimo quadrimestre, arriviamo alla formula
M = C(1 + i/3)3
Se suddividiamo il calcolo, in generale, per un intervallo di tempo n, avremo:
M = C(1 + i/n)n
Nel nostro esempio precedente, che ora riprendiamo, avevamo i = 1.
Calcoliamo, a questo punto, l’interesse composto non mensilmente ma quotidianamente .
In un anno avremo il Montante composto
M = 1 000 000 x (1 + 1/365)365 = 2 714 567 dollari
Immaginiamo ancora che l’interesse composto venga calcolato ad ogni istante , il che equivale a dire che
suddividiamo l’anno in un numero di intervalli tendente all’infinito.
Contrariamente a quello che si potrebbe ingenuamente pensare, non avremo un montante infinito.
Ma il limite di (1 + 1/n)n, con n molto grande, è ancora una somma ragionevole:
= 2,718281828459045235360287… = e
Nel nostro esempio, avremo quindi, all’incirca, la somma di 2 718 282 dollari
. Con questo nuovo, ideale sistema bancario, la tabella del fortunato Paperone diventa:
0
Anni
Montante 1
1
e
2
e2
3
e3
4
e4
5
e5
Ovviamente si può calcolare per curiosità, dopo quanto tempo (in anni) il capitale risulta, invece,
raddoppiato, risolvendo l’equazione
1000000*et = 2000000 → et = 2→ t = ln 2 = 0,693 … (circa 8 mesi)
Questo intervallo di tempo prende il nome di tempo di raddoppio T2, nel senso che la somma raddoppia ogni
volta che sia trascorso un tempo pari a T2
Anni
Montante
0 0,693 1,386 2,079 2,773 3,466
1
2
4
8
16
32
Un ragionamento analogo può essere ripetuto relativamente ad ogni fenomeno che si può studiare con un
modello esponenziale del tipo
La grandezza Y varia secondo le potenze di una base <<a>> la cui scelta dipende dalla scelta dell’intervallo
di tempo dopo il quale vengono <<misurati>> i valori di Y.
Se la rilevazione è <<istantanea>> la base diventa naturalmente il numero e