Bono Marco
Spirali triangolari e quadrate
1
Spirali “triangolari” e “quadrate”
Spirali “triangolari”
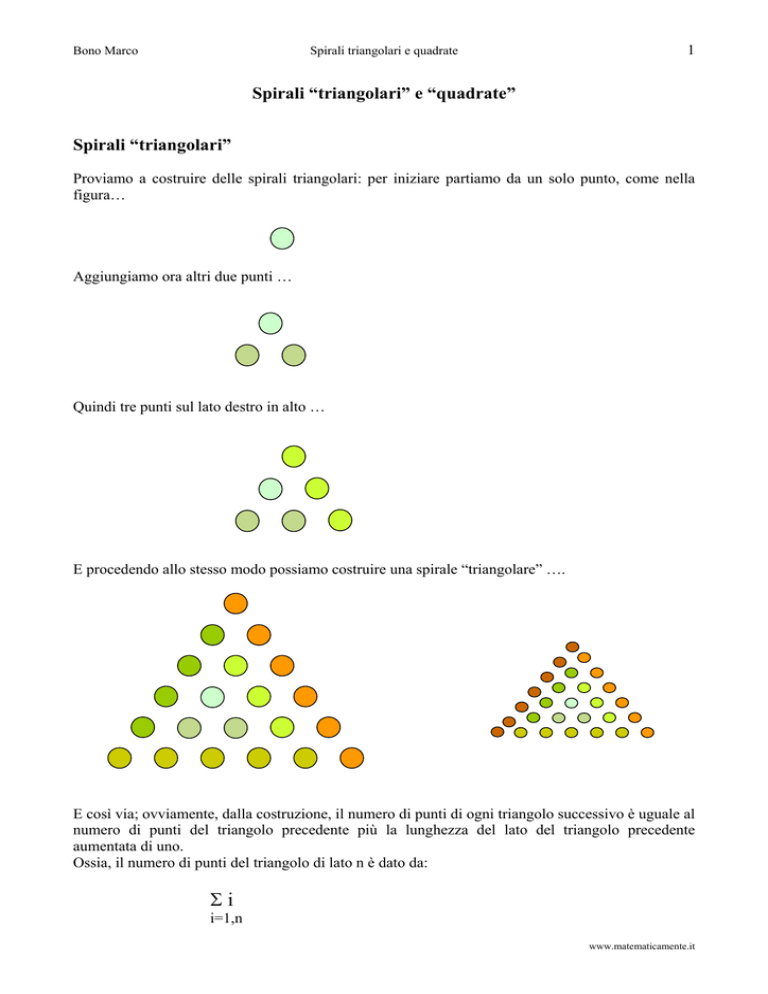
Proviamo a costruire delle spirali triangolari: per iniziare partiamo da un solo punto, come nella
figura…
Aggiungiamo ora altri due punti …
Quindi tre punti sul lato destro in alto …
E procedendo allo stesso modo possiamo costruire una spirale “triangolare” ….
E così via; ovviamente, dalla costruzione, il numero di punti di ogni triangolo successivo è uguale al
numero di punti del triangolo precedente più la lunghezza del lato del triangolo precedente
aumentata di uno.
Ossia, il numero di punti del triangolo di lato n è dato da:
Σi
i=1,n
www.matematicamente.it
Bono Marco
Spirali triangolari e quadrate
2
Spirali “quadrate”
Proviamo a costruire ora delle spirali quadrate: per iniziare partiamo da un solo punto, come nella
figura…
Costruiamo un quadrato con la seguente regola: spostiamo il punto in basso e aggiungiamo due
punti a lato, così ….
Ora passiamo al quadrato successivo, applicando la stessa regola … un po’ modificata, ossia
copiamo il lato del quadrato in alto ed aggiungiamone un altro, più lungo di un’unità a sinistra. Il
nuovo quadrato diventa …
Proseguendo con la regola indicata possiamo ottenere i quadrati successivi ..
Volendo esprimere la regola in formato matematico si ottiene la formula seguente:
Q = 1 + (1+2) + (2+3) + (3+4) + ….
Da questa formula risulta evidente che i numeri nelle parentesi sono i successivi numeri dispari e
quindi, per passare da un quadrato all’altro, occorre sommare un numero dispari.
Se raggruppiamo i numeri della formula precedente in modo diverso otteniamo:
www.matematicamente.it
Bono Marco
3
Spirali triangolari e quadrate
Q = (1+1) + (2+2) + (3+3) + …. + (n+n) + (n+1)
Ossia :
Q = 2*Σ i + (n+1) = Σ i + (Σ i + n+1)
i=1,n
Ma
i=1,n
i=1,n
Σi
è l’n-esimo numero triangolare, mentre Σ i + n+1 è l’n+1-esimo numero
i=1,n
i=1,n
triangolare, quindi un quadrato è esprimibile come somma di due numeri triangolari successivi.
D’altra parte è possibile dimostrare questa proprietà anche in modo grafico:
=
www.matematicamente.it
Bono Marco
Spirali triangolari e quadrate
4
Piramidi di palle
Piramidi quadrate
Immaginiamo di disporre di un certo numero di palle di cannone e, per il nostro amore dell’ordine,
di volerle accatastare in modo da occupare meno spazio.
Come prima idea proviamo a costruire delle piramidi a base quadrata; iniziamo quindi a formare il
primo piano di palle: un quadrato di lato … diciamo 5
Ora passiamo al secondo piano; queste palle andranno ad occupare gli avvallamenti che si trovano
in mezzo a quattro palle contigue. In questo modo il secondo piano sarà un quadrato di lato 4:
Che, sovrapposto al primo piano inizia a formare la piramide:
Ora passiamo al terzo piano; queste palle andranno ad occupare gli avvallamenti che si trovano in
mezzo a quattro palle contigue. In questo modo il terzo sarà un quadrato di lato 3:
www.matematicamente.it
Bono Marco
Spirali triangolari e quadrate
5
E la piramide diventa:
E, continuando così, la piramide finale diventa:
Quante palle siamo riusciti ad ordinare?
E’ facile: abbiamo sovrapposto 5 quadrati di lato progressivamente minore, da 5 a 1. Quindi il
numero di palle è: 52 + 42 + 32 + 22 + 12 = 25 + 16 + 9 + 4 + 1 = 55 palle.
Più in generale la formula per ottenere il numero di palle in una piramide di base quadrate in
funzione del lato della base è:
N=
Σ i2
i=1,n
www.matematicamente.it
Bono Marco
6
Spirali triangolari e quadrate
Piramidi triangolari
Vediamo ora cosa succede se volessimo raggruppare le palle su una piramide a base triangolare.
Per iniziare, come per la piramide a base quadrata, partiamo da un triangolo di base 5:
A questo punto passiamo al triangolo successivo che si formerà nei punti centrali rispetto a tre palle
contigue:
Continuando in questo modo si arriverà a costruire la piramide completa:
Di quante palle sarà composta?
Per rispondere a questa domanda è sufficiente osservare che ogni piano della piramide è un numero
triangolare e ogni piano confinante è costituito da due numeri triangolari successivi. Ora, come
visto al punto “Spirali quadrate”, la somma di due numeri triangolari successivi dà un numero
quadrato (es. T5 (il 5° numero triangolare) + T4 = Q5 (il 5° numero quadrato): 15 + 10 = 25).
Quindi la nostra piramide sarà formata da:
T5 + T4 + T3 + T2 + T1 = Q5 + Q3 + Q1 = 25 + 9 + 1 = 35 palle
www.matematicamente.it
Bono Marco
Spirali triangolari e quadrate
7
In generale la formula per ottenere il numero di palle di una piramide a base triangolare (che ormai
abbiamo riconosciuto essere un tetraedro) in funzione del lato n della base, è la seguente:
2
PT = Σ i
i=n,[2|1],-2
Ossia occorre sommare tutti i quadrati, a partire da n2 fino a 4 = 22 (se n è pari) o 1 (se n è dispari)
con passo 2.
Triangoli di triangoli
Immaginiamo di partire da un triangolo qualsiasi:
Suddividiamolo ora in un numero arbitrario di triangoli simili più piccolini spostando i lati del
triangolo di partenza parallelamente a se stessi quante volte vogliamo:
Quant’è il numero totale di triangolini piccoli?
Per rispondere a questa domanda osserviamo che il triangolo composto è formato da due tipi di
triangoli: il primo tipo è esattamente uguale al triangolo di partenza, anche come orientazione, il
secondo tipo è sempre uguale al triangolo di partenza ma ribaltato: il vertice in alto si trova in
basso, quello di destra si trova a sinistra e viceversa.
Per visualizzare meglio questi triangoli coloriamo il primo tipo in rosso ed il secondo in blu; la
figura precedente diventa:
www.matematicamente.it
Bono Marco
Spirali triangolari e quadrate
8
Ora si può osservare che sia il numero di triangoli rossi che il numero di triangoli blu sono dei
numeri triangolari, anzi, in particolare, il numero triangolare di triangoli rossi è il numero
triangolare successivo del numero triangolare di triangoli blu. Ad esempio, nella nostra figura il
numero di triangoli rossi è 21 (che è il 6° numero triangolare) e il numero di triangoli blu è 15 (che
è il 5° numero triangolare)
A questo punto, grazie alla proprietà dei numeri triangolari successivi che, sommati tra di loro,
danno un quadrato (vedasi il punto “Spirali quadrate”), ossia, con ovvio significato dei simboli:
Tn + Tn-1 = Qn
possiamo concludere che, a seguito della suddivisione di un triangolo in un numero arbitrario di
triangolini più piccoli, il numero di triangolini è sempre un quadrato, in particolare è il quadrato del
numero di triangolini della base del triangolo grande.
Nel nostro esempio, avendo 6 triangolini su un lato del triangolo grande, abbiamo 21 triangolini
rossi più 15 triangolini blu, ossia complessivamente 36 (= 62) triangolini.
www.matematicamente.it