Rappresentazione dei dati

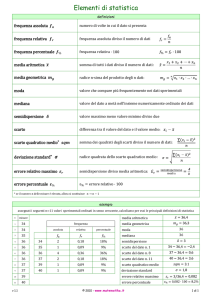
STATISTICA E PROBABILITÀ
La statistica è il ramo della matematica che studia i fenomeni collettivi. Gli avvenimenti e i
fenomeni di cui si occupa la statistica sono detti fenomeni statistici. Ci sono 4 fasi nello studio di
un evento statistico:
1.
2.
3.
4.
Rilevamento dati
Elaborazione dati
Rappresentazione dati
Conclusioni
Rilevamento dati
Consiste nel raccogliere e classificare i dati relativi ad un fenomeno.
Def.
L’insieme di dati raccolto si chiama campione statistico.
Da un campione statistico si possono calcolare diverse grandezze:



Frequenza assoluta𝑓𝑎 di un dato statistico: numero di volte in cui esso si presenta
Frequenza relativa𝑓𝑟 di un dato statistico: rapporto tra frequenza assoluta e numero totale
di casi esaminati.
Frequenza percentuale: è la frequenza relativa trasformata in percentuale.
Frequenza cumulata
La frequenza cumulata si ottiene addizionando a una frequenza tutte le frequenze che la
precedono.
Esempio:
Temp. (°C)
-5
-4
-3
-2
-1
0
1
2
Totali
Frequenza assoluta
7
12
9
7
5
5
3
2
50
Frequenza relativa
0,14
0,24
0,18
0,14
0,1
0,1
0,06
0,04
1
Frequenza percentuale
14%
24%
18%
14%
10%
10%
6%
4%
100%
1
Temp. (°C)
-5
-4
-3
-2
-1
0
1
2
Fr. Ass. CUMULATA
7
19
28
35
40
45
48
50
Fr. Rel. CUMULATA
0,14
0,38
0,56
0,7
0,8
0,9
0,96
1
Elaborazione dati
Consiste nel trasformare i dati raccolti in dati matematici, detti INDICATORISTATISTICI:
MEDIA ARITMETICA SEMPLICE:
è la somma di tutti i dati, diviso il numero di dati.
𝑀=
𝑎1 + 𝑎2 + ⋯ + 𝑎𝑛
𝑛
Esempio:
Voti Luca a fine anno:
ita: 9; mat:8; geo:6; sto:10; musica: 7; arte: 6; ingl: 8; fra:7; tecn:7
𝑚=
9 + 8 + 6 + 10 + 7 + 6 + 8 + 7 + 7 68
=
= 7,5
9
9
MEDIA ARITMETICA PONDERATA:
Si moltiplica ogni dato per il suo peso (che in genere è la sua frequenza), si somma il tutto e poi si
divide per il totale dei pesi.
𝑀𝑃 =
𝑝1 ∙ 𝑎1 + 𝑝2 ∙ 𝑎2 + ⋯ + 𝑝𝑛 ∙ 𝑎𝑛
𝑝1 + 𝑝2 + ⋯ + 𝑝𝑛
Esempio:
un negozio compra delle mele da 3 fornitori diversi:
1. 200 kg costano 2€/kg
2. 300 kg costano 1,5€/kg
3. 50 kg costano 4€/kg
il prezzo medio delle mele è:
𝑝1 ∙ 𝑎1 + 𝑝2 ∙ 𝑎2 + 𝑝3 ∙ 𝑎3 200 ∙ 2 + 300 ∙ 1,5 + 50 ∙ 4 1050
𝑀𝑃 =
=
=
= 1,91 €/kg
𝑝1 + 𝑝2 + 𝑝3
200 + 300 + 50
550
2
MEDIANA o dato centrale:
è la posizione centrale in una successione di dati scritti in ordine crescente.
Se i dati sono in numero pari, si devono cercare i 2 dati centrali e farne la media aritmetica.
Esempio:
voti di scienze: 7 5 9 6 8 10 6 7 4 8 9
Ordino i voti dal più piccolo al più grande:
4
5
6
6
7
7
8
8
9
9 10
Il dato centrale è 7.
Esempio:
voti di scienze: 5 5 9 6 8 10 6 7 4 8
Orndino i voti dal più piccolo al più grande:
4
5
5
6
6
7
8
8
9
10
Dato che i valori centrali sono 2, per ottenere la mediana di deve fare la media aritmetica tra i due:
𝑀=
6 + 7 13
=
= 6,5
2
2
MODA:
è il valore che si ripete più frequentemente.
3
Rappresentazione dei dati
Classi aventi la stessa ampiezza
Immaginiamo di aver raccolto i dati relativi alle altezze di tutti gli studenti della nostra scuola (100)
e di averli raccolti in questa tabella:
Classi di altezza in cm
Frequenza assoluta
Ampiezza della classe
140-145
145-150
150-155
155-160
160-165
165-170
14
11
15
13
16
10
145 – 140 = 5
150 – 145 = 5
155 – 150 = 5
160 – 155 = 5
165 – 160 = 5
170 – 165 = 5
170-175
175-180
180-185
8
7
6
175 – 170 = 5
180 – 175 = 5
185 – 180 = 5
Oss.
Numero di studenti
Classe 155-160 significa che il primo numero appartiene alla classe, mentre il secondo non vi
appartiene! Ossia se 𝑥 è un dato che appartiene a tale classe, allora 155 ≤ 𝑥 < 160.
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
y
140-145
145-150
150-155
155-160
160-165
165-170
170-175
175-180
180-185
x
Altezza in cm
La frequenza è DIRETTAMENTE PROPORZIONALE all’ALTEZZA DEI RETTANGOLI dell’istogramma,
che hanno tutti la stessa base. La classe con altezza più alta è quella che ha frequenza maggiore!
Le classi con frequenza più alta si chiamano CLASSI MODALI.
4
Classi aventi ampiezza diversa
Immaginiamo di aver raccolto i dati relativi ad una serra con 320 piante distribuite secondo
l’altezza in questa tabella:
Classi di altezza in cm
Frequenza assoluta
Ampiezza della classe
100-105
105-110
110-120
120-130
130-135
135-140
140-145
20
30
90
60
40
35
25
100 – 105 = 5
105 – 110 = 5
120 – 110 = 10
130 – 120 = 10
135 – 130 = 5
140 – 135 = 5
145 – 140 = 5
Altezza rettangoli
(frequenza:ampiezza)
4
6
9
6
8
7
5
145-150
20
150 – 145 = 5
4
La base dei rettangoli è direttamente proporzionale all’ampiezza della classe, l’altezza è
direttamente proporzionale al rapporto tra la frequenza e l’ampiezza.
5
Analisi della dispersione
L’analisi della dispersione ci indica quanto i dati sono concentrati vicino alla media o al valore
centrale.
Def.
Si definisce scarto assoluto di un valore statistico rispetto alla media aritmetica il valore assoluto
della differenza fra la media aritmetica del campione e il valore statistico considerato.
𝑠𝑐𝑎𝑟𝑡𝑜 = |𝑀 − 𝑎𝑖 |
esempio:
riportiamo nella seguente tabella il numero di pezzi difettosi realizzati da un macchinario in 10
giorni:
Giorno
Numero pezzi difettosi
Scarto assoluto rispetto alla media
1
9
|5 − 9| = 4
2
3
|5 − 3| = 2
3
5
|5 − 5| = 0
4
5
|5 − 5| = 0
5
3
|5 − 3| = 2
6
0
|5 − 0| = 5
7
5
|5 − 5| = 0
8
2
|5 − 2| = 3
9
8
|5 − 8| = 3
10
10
5
|5 − 10| = 5
MEDIA
2,4
Def.
Si definisce SCARTO MEDIO ASSOLUTO la media degli scarti assoluti dei singoli dati.
6