1
0.0.1
Esercizio Q1, Prima prova in itinere del 16 novembre 2009, prof. Dario d’Amore
R1
R1 = 7Ω,R2 = 5Ω,R3 = 8Ω
Scrivere la soluzione richiesta in funzione del parametro E
E
V2
R2
Risultato
v2 = E ·
0.0.2
R2
R1 +R2 +R3
5
= E 7+5+8
=
E
4
R3
Esercizio Q2, Prima prova in itinere del 16 novembre 2009, prof. Dario d’Amore
Le correnti nei tre rami di collegamento dei due tripoli
C1 e C2 risultano essere:
i1 = 5mA, i3 = 12mA
determinare i2
i1
i2
C1
C2
Risultato.
i3
i1 + i2 + i3 = 0 ⇒ i2 = −5mA − 12mA = −17mA
0.0.3
Esercizio Q3, Prima prova in itinere del 16 novembre 2009, prof. Dario d’Amore
A
R0
B
0.0.4
Quanto vale la resistenza equivalente vista ai morsetti
AB del circuito di figura, sapendo che R0 = 50Ω?
Risultato:
RAB = n2 R0 = 100 · 50Ω = 5kΩ
10:1
Esercizio E1, Prima prova in itinere del 16 novembre 2009, prof. Dario d’Amore
0.0.4.1
Testo:
i1 A
E1
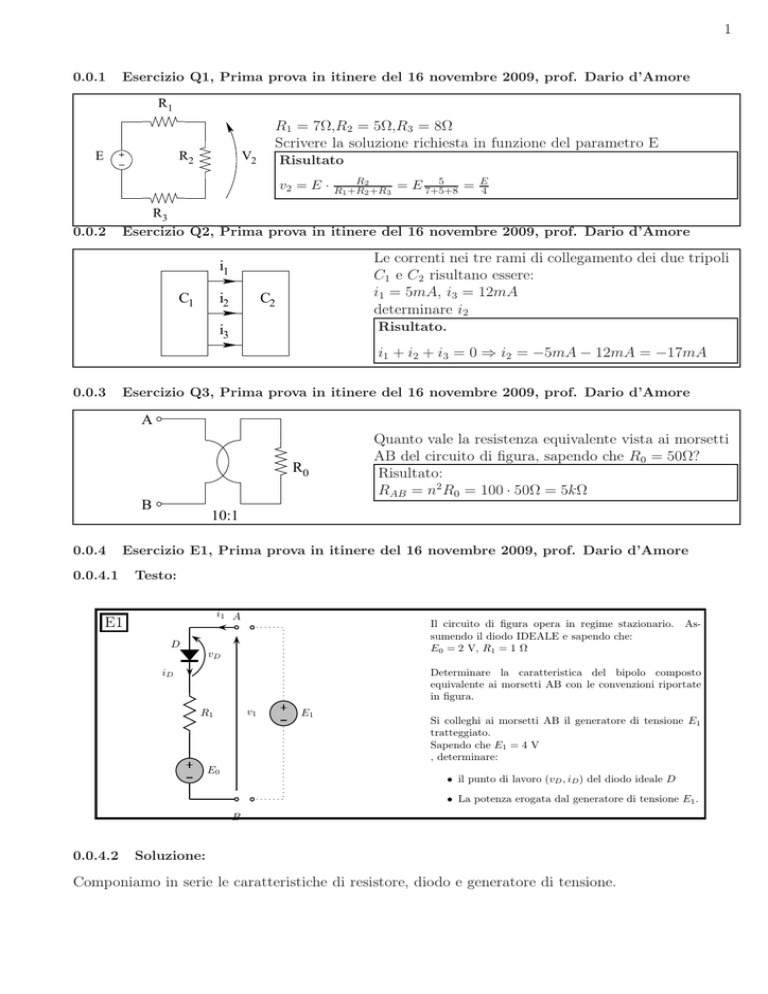
Il circuito di figura opera in regime stazionario. Assumendo il diodo IDEALE e sapendo che:
E0 = 2 V, R1 = 1 Ω
D
vD
Determinare la caratteristica del bipolo composto
equivalente ai morsetti AB con le convenzioni riportate
in figura.
iD
v1
R1
E0
E1
Si colleghi ai morsetti AB il generatore di tensione E1
tratteggiato.
Sapendo che E1 = 4 V
, determinare:
• il punto di lavoro (vD , iD ) del diodo ideale D
• La potenza erogata dal generatore di tensione E1 .
B
0.0.4.2
Soluzione:
Componiamo in serie le caratteristiche di resistore, diodo e generatore di tensione.
2
I
I
I
V
V
I
I
I
2V
V
V
V
V
Colleghiamo ora il generatore E1 utilizzando il metodo i soluzione grafica del circuito elementare
otteniamo:
I
2A
2V
4V V
Nota la corrente nel circuito (2A), sappiamo che anche nel diodo passeranno 2A. Di conseguenza
il suo punto di lavoro sarà:
(vD ,id ) = (0V, 2A).
Potenza erogata dal generatore di tensione E1 :
Nota la sua corrente (2A) e la tensione ai suoi capi otteniamo:
P = 4V · 4A = 8W .
Tale potenza è erogata in quanto tensione e corrente sono espresse con la convenzione dei generatori.
3
0.0.5
Esercizio E2, Prima prova in itinere del 11 Novembre 2009, prof. Dario d’Amore
0.0.5.1
Testo
E2
R2
A
R1
Sapendo che:
R1 = 2 Ω, R2 = 8 Ω, gm = 2 Ω−1 , A = 1 A
A
• Determinare il circuito equivalente di Thevenin ai
morsetti AB per il bipolo composto riportato in
figura.
gm vc
vc
• Dire, motivando la risposta, se esiste anche il circuito equivalente di Norton.
B
SVIPUPPARE L’ESERCIZIO QUI’ SOTTO
Soluzione:
Calcoliamo innanzitutto il valore di tensione del generatore equivalente serie, calcolando la tensione
a circuito aperto.
gmVC R2
VC
R1
R1 VC
1A
0
A
gmVC
vAB
B
Cerchiamo innanzitutto di calcolare il valore della pilotante:
• La corrente in R2 sarà pari alla corrente del generatore pilotato gm Vc .
• La corrente in R1 è pari a
VC
R1
Con una LKI al nodo C otteniamo:
Vc
+ 2Ω−1 VC → 1A = 25 VC → Vc = 25 V = 0.4V
1A = 2Ω
Noto il valore della pilotante, calcoliamo la tensione VAB
VAB = VC − gm VC R2 = 52 − 2 · 8 · 52 = 2−32
= −6V
5
Calcolo del valore di resistenza equivalente.
Utilizziamo il metodo del generatore di sonda.
Dovendo calcolare l’equivalente di tipo serie utilizziamo un generatore di sonda di corrente.
R2
IS
A
R1 VC
IS
gmVC
VS
B
4
Cerchiamo innanzitutto la pilotante. Essa sarà pari a:
VC = R1 · (IS − gm VC )
ovvero
VC (1 + gm R1 ) = R1 IS
2
VC = 1+gRm1 R1 IS = 1+4
IS = 52 IS
La corrente in R1 sarà quindi
2
I
IR1 = VRC1 = 52ΩS = 51 IS
La tensione VAB sarà quindi
VAB = 15 IS · (R1 + R2 ) = 2IS
Otteniamo quindi
Req = 2IISS = 2Ω
In alternativa, si poteva utilizzare un generatore di sonda di tensione, supponendo che esista
anche l’equivalente di tipo parallelo del circuito. Si noti che se riusciamo a calcolare il valore di
resistenza equivalente con tale generatore esisterà sicuramente anche il circuito equivalente di Norton.
Spegnamo quindi i generatori impressivi.
R2
R1 VC
VS
R1+R2 IS
A
gmVC
VS
B
La pilotante si ottiene rapidamente utilizzando un partitore di tensione.
2
1
VC = Vs R1R+R
= Vs 8+2
= V5S
2
La corrente nel generatore pilotato sarà quindi
IGP = gm Vc = 2V5S
La corrente nella serie di R2 ed R1 sarà:
s
IR2 = R1V+R
= V10S
2
quindi la corrente IS (LKI al nodo in alto a destra) sarà:
5
Vs = V2S
IS = V10S + 2V5S = 10
da cui
Req = VIss = 2Ω
Il circuito equivalente di Norton esiste, in quanto esiste l’equivalente di thevenin e la resistenza equivalente è diversa da zero. E’ possibile quindi ottenere tale equivalente utilizzando la
trasformazione dei generatori.
5
0.0.6
Esercizio E3, Prima prova in itinere del 16 novembre 2009, prof. Dario d’Amore
0.0.6.1
Testo
E3
Si consideri l’OPAMP IDEALE ed il circuito operante
in regime stazionario. Sapendo che:
E = 500 mV
R1 = 1 kΩ, R2 = 1 kΩ, R3 = 10 kΩ, R4 = 500 Ω
Determinare:
• La tensione vo ai capi di R4
• La potenza assorbita dal resistore R4
• La potenza erogata dall’OPAMP
Immaginando di voler rappresentare la parte tratteggiata
come doppio bipolo, determinarne (se esiste) la rappresentazione controllata in corrente (Matrice R)
R3
R1
OP AM P
E
R2
vo (t) R4
0.0.6.2
Soluzione
R3
E
0
E
E
R1
R1
0
R2
0
0
0
R4
R3
E
R1
LKI
0
E
E
R1
R1
0
R2
E
R3 R
1
0
R4
6
R3
E
R3 R
1
E
0
E
R3 R
1
R4
Otteniamo quindi
Vo = −0.5[V ] · 10kΩ
= 5V
1kΩ
La potenza assorbita dal resistore R4 è pari a:
V2
25
= 50mW
PR4 = VR4 · IR4 = VR4 · VRR44 = RR44 = 500
Per calcolare la potenza erogata dall’amplificatore operazionale, dobbiamo conoscerne corrente e
tensione di uscita. La tensione di uscita è pari a VR4 (già calcolata), mentre la corrente è ottenibile
da una LKI sul nodo di uscita dell’operazionale.
IR4 = − VRR44 = 10mA (con le convenzioni di segno in figura)
5V
= 0.5mA La corrente della porta di uscita dell’amplificatore operazionale è
IR3 = VRR33 = 10kΩ
quindi:
IOA = 10.5mA
R3
E
R3 R
1
0.5mA
10mA
−5V
quindi la potenza erogata dall’amplificatore operazionale sarà:
· 10.5mA
(
−5V
POA =
−
| {z } ) = 52.5mW
| {z }
|{z}
convenzione utilizzatori tensione sull′ uscita corrente di uscita
R4
Per ottenere la rappresentazione controllata in corrente, dobbiamo esprimere V1 e V2 in funzione
delle correnti I1 ed I2 . Per questo doppio bipolo abbiamo.
3
V
V2 = − R
R1 1
e
I1 = RV11 → V1 = R1 I1
Sostituendo la seconda nella prima otteniamo
(
V1 = R1 I1
V2 = −R3 I1
la quale è la rappresentazione controllata in corrente.
La matrice R sarà quindi
R=
"
R1 0
−R3 0
#









