Triangoli: confronto di angoli e di segmenti

Classe prima Liceo Scientifico-Gli utenti registrati trovano le risoluzioni dei problemi nella sezione
Geometria\Geometria Razionale
Triangoli: confronto di angoli e di segmenti
(applicazione del primo teorema dell’angolo esterno per un triangolo)
Problema_1-Sia ABC un triangolo qualsiasi e P un punto interno allo stesso. Considerata la semiretta di
origine B e passante per P, sia D il punto in cui essa interseca il lato AC. Congiungere P con il vertice C.
Dimostrare che l’angolo BPC è maggiore dell’angolo BAC.
***
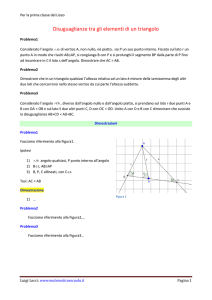
Problema_2-Considerata nel piano una retta r sia P un punto non appartenente ad r ed M la proiezione
ortogonale di P su r. Fissare su r due punti A e B da parti opposte rispetto ad M, con MA<MB e unire P
con A e B. Dimostrare che PA<PB.
***
Problema_3-Si consideri nel piano un angolo acuto rOs e sia P un qualsiasi punto interno all’angolo.
Indicato con A il punto sulla semiretta r tale che OAOP, tracciare la semiretta t di origine A e passante
per P.
i)
ii)
Dimostrare che la semiretta t interseca il secondo lato s dell’angolo rOs .
Detto B il punto di intersezione tra t ed s, dimostrare che OB>OA
Luigi Lecci: www.matematicaescuola.it
Pag. 1