Mo# con accelerazione costante che la velocità varia in modo lineare nel
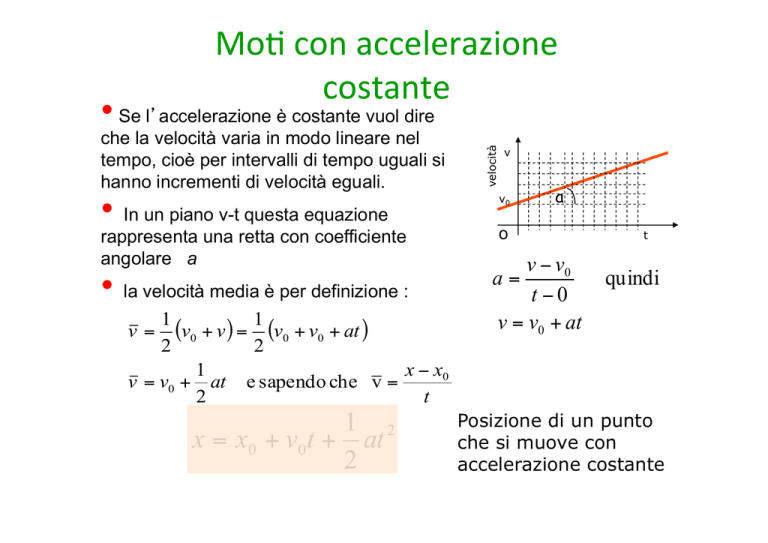
tempo, cioè per intervalli di tempo uguali si
hanno incrementi di velocità eguali.
• In un piano v-t questa equazione
rappresenta una retta con coefficiente
angolare a
• la velocità media è per definizione :
1
(v0 + v ) = 1 (v0 + v0 + at )
2
2
x − x0
1
v = v0 + at e sapendo che v =
2
t
v=
1 2
x = x0 + v0 t + at
2
velocità
• Se l’accelerazione è costante vuol dire
v
v0
a
o
v − v0
a=
t −0
v = v0 + at
t
quindi
Posizione di un punto
che si muove con
accelerazione costante
L’equazioni del moto con a = cost • Il moto con a = cost è descritto da
cinque grandezze
x, v, t, a, v0,
Tali grandezze si ottengono dalle
due equazioni della precedente
diapositiva.
§ Il moto con accelerazione
costante più comune è il moto di un
grave in caduta libera
§ al livello del mare l’accelerazione di
gravità è
g = 9,806 + 0,017 m/s2
v = v0 + at
1 2
x = x0 + v0 t + at
2
v 2 = v02 + 2a (x − x0 )
1
x = x0 + (v0 + v )t
2
1 2
x = x0 + vt − at
2
x
v
t
a
v0
Caduta di un grave
• In prossimità della superficie terrestre ogni
corpo è soggetto ad una accelerazione costante
pari a 9,81 m/s2.
Quindi l’equazione oraria y = f(t) di un oggetto
lasciato libero di muoversi è:
y = -1/2 gt2
• Il segno meno deriva dall’orientazione del
sistema di riferimento che è definita positiva
uscendo dalla superficie della Terra.
• Se l’oggetto parte da una posizione y0 e se ha
una sua velocità iniziale v0 allora l’equazione
oraria si completa nel seguente modo
y = y0 + v0t -1/2 gt2
Moto in più dimensioni I moti in più dimensioni
si ottengono sommando
vettorialmente i moti
lungo ciascun asse 〈v 〉 =
r = xi + yj + zk ⇒ Δr = r2 − r1
Δr = ( x2i + y2 j + z 2 k ) − ( x1i + y1 j + z1k )
Δr = (x2 − x1 )i + ( y2 − y1 ) j + (z 2 − z1 )k
Δr = Δxi + Δyj + Δzk
Δr
dr
⇒v=
Δt
dt
d
dx
dy
dz
v = (xi + yj + zk ) =
i+
j+ k
dt
dt
dt
dt
v = vxi + v y j + vz k
Δv
dv
⇒a =
Δt
dt
dv y
dv x
dv z
a=
i+
j+
k
dt
dt
dt
a = axi + a y j + az k
〈a 〉 =
Moto di un proie8le La vy varia passando da positiva,
a nulla, a negativa, mentre la vx
è sempre costante
§ Un corpo viene lanciato in prossimità
della superficie terrestre con una
velocità iniziale V0, le cui componenti
sono V0x eV0y.
§ Nel suo progredire il proiettile risentirà,
solo, della forza di gravità che gli imprime
una accelerazione pari a: g = - 9.81 m/s2
Traie:oria di un proie8le • Il moto orizzontale e quello ver#cale sono due mo# indipenden# e possono essere tra:a# ciascuno per conto proprio. • Lungo l’asse x il moto è un moto re8lineo uniforme, mentre lungo l’asse y il moto è uniformemente accelerato. x = x0 + v0 xt
⇒
1 2
y = y0 + v0 y t − gt ⇒
2
x = x0 + v0 cosθ 0t
1 2
y = y0 + v0 senθ 0t − gt
2
La traie:oria di un proie8le x
t=
v0 cosθ 0
&
# 2
g
y = [tgθ 0 ] x − $
!x
% 2(v0 cosθ 0 )"
parabola
400
Y (metri)
§ Ricavando t dalla equazione del moto re2lineo uniforme, supponendo x0 = y0 = 0, e sos;tuendo nell’equazione nel moto uniformemente accelerato si o2ene: 300
200
100
0
0
10
20
30
X (metri)
Si riconosce l’equazione di una parabola nel piano x,y con la concavità rivolta verso il basso (y = -­‐ ax2 + bx) 40
GiFata • La gi:ata è la distanza orizzontale coperta da un proie8le. • L’equazione della traie:oria si ricava dalle: x − x0 = v0 (cos θ 0 )t
y − y0 = v0 senθ 0 t −
1 2
gt
2
• chiamiamo x-­‐x0 = R e poniamo y-­‐y0 = 0 R = v0 (cos θ 0 )t
1
0 = v0 senθ 0t − gt 2
2
le cui soluzioni sono
v02
v02
R = 2 sin θ 0 cos θ 0 ⇒ R = sin(2θ 0 )
g
g
t =0
〈 t = 2v0 sin θ 0
g
R è massima a
θ0 = 45°
Altezza massima • L’altezza massima raggiunta da un proie8le si calcola sfru:ando le equazioni del moto g
2
y = (tan θ 0 ) x −
x
2
2(v0 cosθ 0 )
R = v0 (cos θ 0 )t
1
0 = v0 senθ 0 t − gt 2
2
le cui soluzioni sono
v02
v02
R = 2 sin θ 0 cos θ 0 ⇒ R = sin(2θ 0 )
g
g
t=0
〈 t = 2v0 sin θ 0
g
R è massima a
θ0 = 45°












