Diedro

Geometria euclidea dello spazio
Presentazione n. 3
Diedri e
perpendicolarità tra piani
Prof. Daniele Ippolito
Liceo Scientifico “Amedeo di Savoia” di Pistoia
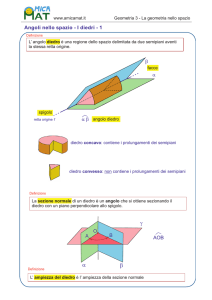
Diedro
Si dice diedro ciascuna delle due parti di spazio divise da due
semipiani aventi l’origine in comune, inclusi i semipiani stessi.
I due semipiani si dicono facce del
diedro.
La retta comune alle due facce si
dice spigolo del diedro.
diedro 1
r
diedro 2
I punti di un diedro non
appartenenti alle facce si dicono
interni al diedro.
I
punti
dello
spazio
non
appartenenti al diedro si dicono
esterni al diedro.
.
A
.B
diedro convesso
Due semipiani secanti aventi la
stessa origine e non complanari
individuano un diedro convesso ed
un diedro concavo.
diedro
concavo
Nella maggior parte dei casi, quando si parla del diedro
individuato da due semipiani, si sottintende il diedro convesso.
Sezione normale di un diedro
Si dice sezione normale di un
diedro l’angolo che si ottiene
intersecando il diedro con un
piano perpendicolare allo spigolo.
b
b
O
a
r
aôb: sezione normale
Teorema sulla congruenza delle sezioni normali
1) Due sezioni normali di
uno stesso diedro sono
congruenti.
b’
b
b
a’
O’
O
a
r
’
2) Due
diedri
sono
congruenti se e solo se
hanno sezioni normali
congruenti.
Si dice ampiezza di un
diedro l’ampiezza di una sua
sezione normale.
Semipiano bisettore di un diedro
c
b
Si dice semipiano bisettore di un
diedro il semipiano che ha come
origine lo spigolo del diedro e che
lo divide in due diedri congruenti.
aôc = côb
r
O
a
Il semipiano bisettore è il luogo di
punti equidistanti dalle facce del
diedro.
Piani perpendicolari
Due
piani
si
perpendicolari
se
quattro diedri retti.
dicono
formano
Teorema di esistenza e unicità di piani perpendicolari
r
Dato un piano
e una retta r
non perpendicolare ad , esiste
uno ed un solo piano
passante per r e perpendicolare
ad .