Le figure solide
Nozioni generali
Un piano nello spazio può essere individuato da:
1. tre punti A, B e C non allineati.
2. una retta r e un punto A non appartenente ad essa.
3. due rette r e s incidenti.
4. due rette r e s parallele.
Le rette complanari possono essere:
1. incidenti, se hanno un solo punto in comune.
2. parallele, se non hanno alcun punto in comune.
3. coincidenti, se hanno tutti i loro punti in comune.
Due rette nello spaio si dicono sghembe se non sono complanari e non hanno alcun punto in comune.
Una retta è perpendicolare ad un piano se lo interseca in un punto e se é perpendicolare ad ogni retta del
piano passante per quel punto.
La distanza di un punto da un piano è il segmento perpendicolare condotto dal punto al piano.
Due piani nello spazio possono essere:
1. incidenti e secanti, se hanno una retta r in comune;
2. paralleli, se non hanno alcun punto in comune;
3. coincidenti, se hanno tutti i loro punti in comune.
Definizioni
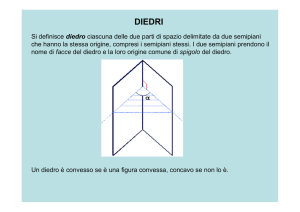
1. Il diedro è ciascuna delle due parti in cui lo spazio rimane diviso da due semipiani aventi la stessa
origine [figura 1]; i due semipiani si dicono facce del diedro, la retta origine si dice spigolo o costola
del diedro.
2. La sezione normale di un diedro é l'angolo che sì ottiene sezionando il diedro con un piano
perpendicolare al suo spigolo.
3. La misura di un angolo diedro è data dall'ampiezza della sua sezione normale.
4. Due diedri si dicono consecutivi quando hanno lo spigolo e una faccia comune.
5. Due diedri consecutivi si dicono adiacenti quando le due facce non comuni sono semipiani opposti.
6. Si dice semipiano bisettore il semipiano che, uscendo dallo spigolo dei diedro, lo divide in due diedri
congruenti.
7. Due piani si dicono perpendicolari se intersecandosi formano quattro diedri congruenti.
8. L'angoloide è la parte di spazio determinata da tre o più angoli aventi il vertice in comune e tutti i lati
a due a due consecutivi. [figura 2]
Proprietà
•
La somma delle ampiezze degli angoli delle facce di un angoloide è sempre minore di un angolo giro.
I poliedri
Definizioni
1. Un poliedro è la parte di spazio delimitata da poligoni posti su piani
diversi in modo tale che ogni lato sia in comune a due di essi. [figura 1]
2. I poligoni che delimitano il poliedro si dicono facce del poliedro.
3. I vertici e i lati di ogni poligono vengono detti rispettivamente vertici e
spigoli del poliedro.
4. I segmenti che uniscono due vertici non appartenenti alla stessa faccia si dicono diagonali.
5. La relazione di Eulero: in ogni poliedro convesso, la somma del numero delle facce e del numero dei
vertici è uguale al numero degli spigoli più due: f + v = s + 2 [figura 2 ].
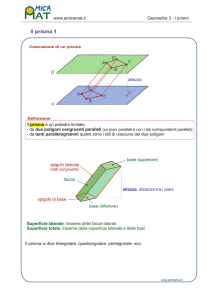
I prismi
Definizioni
1. Il prisma è un poliedro costituito da due poligoni congruenti, posti su
due piani paralleli e con i lati paralleli e da tanti parallelogrammi quanti
sono i lati di ciascuno del due poligoni.
2. I due poligoni posti sui due piani paralleli costituiscono le basi del
prisma i parallelogrammi, compresi fra i due piani costituiscono le facce
laterali dei prisma.
3. L'insieme delle facce laterali e delle basi costituiscono la superficie
totale del prisma.
4. La distanza tra le due basi costituisce l’altezza del prisma.
5. Un prisma è retto se gli spigoli laterali sono perpendicolari ai piani delle
basi. [figura 1]
6. Un prisma è regolare se è retto e se ha come basi due poligoni regolari.
7. Il parallelepipedo rettangolo è un prisma retto che ha come facce sei
rettangoli a due a due congruenti. [figura2]
Formule
•
•
•
•
L'area della superficie laterale di un prisma retto è uguale al prodotto del perimetro di base per la
misura
Dell’altezza Al = p * h
L’area della superficie totale di un prisma retto si ottiene addizionando all'area laterale il doppio
dell'area di
base.
At = Al + 2Ab
•
Il volume di un prisma retto si ottiene moltiplicando l'area della base per la misura dell’altezza: V=
Ab*h.
•
La misura della diagonale di un parallelepipedo rettangolo è uguale alla radice quadrata della somma
dei quadrati della misure delle tre dimensioni: d = a 2 + b 2 + c 2
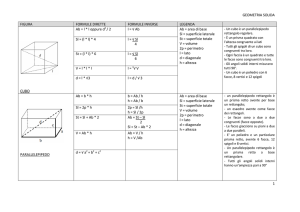
Il cubo
Definizione
1. Il cubo è un parallelepipedo rettangolo avente le tre dimensioni
congruenti e come facce sei quadrati congruenti. [figura 1]
Formule
•
•
•
•
L’area della superficie laterale di un cubo è uguale a quattro volte l'area di una faccia: Al = 4 * l2
L'area della un superficie totale di un cubo è uguale a sei volte l’area di una faccia: At = 6 * l2.
Il volume di un cubo si ottiene elevando alla terza potenza la misura del suo spigolo: V = 13.
La diagonale di un cubo è data da: d = l * 3
La piramide
Definizioni
1. La piramide è la parte di spazio compresa in un angoloide delimitata dal vertice e da un piano non
passante per il vertice
2. Una piramide si dice retta se nella base si può inscrivere una
circonferenza e il piede dell'altezza coincide col centro di questa
circonferenza. [figura 1]
3. L’apotema di una piramide retta è l'altezza di uno qualunque dei triangoli
che costituiscono le sue facce laterali.
4. Una piramide è regolare se è retta e se ha come base un poligono regolare.
Formule
•
L'area della superficie laterale di una piramide retta é uguale al prodotto del perimetro della base per
la misura dell'apotema e diviso due: Al = p * a : 2
•
L'area della superficie totale di una piramide si ottiene addizionando all'area laterale l'area di base:
At =Al + Ab
•
Il volume di una piramide è uguale ad un terzo del prodotto dell'area di base per la misura dall'altezza.
V = Ab * h : 3.
Il cilindro
Definizione
1. Si dice cilindro il solido generato dalla rotazione completa di un rettangolo
attorno ad uno dei suoi lati. [figura 1]
Formule
2. L'area della superficie laterale di un cilindro è data dal prodotto della
misura della circonferenza di base per l’altezza: Al = 2 * π * r * h [figura
2]
3. L'area della superficie totale di un cilindro è data dalla somma dell’area
laterale e dell’area delle due basi: At = Al + 2*Ab
4. Il volume di un cilindro è dato dal prodotto dell'area del cerchio di base
per la misura dell’altezza: V = π r2 h
Il cono
Definizione
1. Si dice cono il solido generato dalla rotazione completa di un triangolo rettangolo attorno ad uno dei
suoi cateti.
[figura 1]
Formule
o L'area della superficie laterale di un cono è data dal
prodotto della misura della semicirconferenza di
base per la misura dell'apotema: Al = π * r * a
[figura 2]
o
L'area delle superficie totale di un cono è data dalla
somma della superficie laterale con l’area di base:
At = Al + Ab
o I1 volume del cono è dato dalla terza parte del
prodotto dell'area del cerchio di base per la misura
dell’altezza: V = π * r * h : 3