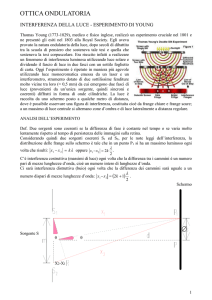
Titolo: Esperimento di Young
Scopo: Determinare la distanza d tra le fenditure nei tre casi
Materiale utilizzato:
Emettitore laser: elio-neon con luce lineare polarizzata
λ= 632,8 nm (•10-9)
P= 1 mW
Calibro per misurare distanza tra fenditure e schermo e tra frange luminose
3 fenditure:
- A: doppia fenditura a sinistra (d molto piccolo)
- B: doppia fenditura centrale (d intermedio)
- C: doppia fenditura a destra (d molto grande)
A
B
C
Distanza tra fenditure
e schermo:
L = 4,92 mm
Procedimento – parte 1
A luci spente e a emettitore acceso, un fascio di luce monocromatica (costituita da un
singolo colore e quindi da una sola lunghezza d’onda) viene fatto passare attraverso la
doppia fenditura A che, essendo in fase, agisce come sorgente coerente (mantiene
reciprocamente una relazione di fase costante) di luce monocromatica, come è richiesto
per produrre interferenza. Dopo essere passata attraverso queste fenditure, la luce forma
su uno schermo lontano una figura di interferenza nella quale si alternano frange luminose
e frange scure.
Osservazioni 1:
Abbiamo misurato la distanza lineare tra una frangia luminosa e l’altra:
y = 5,2 • 10-3m
Procedimento – parte 2:
Abbiamo ripetuto il 1° procedimento attraverso la doppia fenditura B
Osservazioni 2:
Abbiamo misurato la distanza lineare tra una frangia luminosa e l’altra:
y = 1,9 • 10-3m
Procedimento – parte 3:
Abbiamo ripetuto lo stesso procedimento attraverso la doppia fenditura C
Osservazioni 3:
Abbiamo osservato il fenomeno della diffrazione poiché le fenditure sono troppo lontane
e quindi ne consideriamo solamente una. La distanza lineare dalla frangia centrale alla
prima frangia luminosa è:
y = 2,6 • 10-3m
Calcoli:
1. λ = yd
L
Lλ = yd
d = Lλ
y
d = (4,92)(632,8 • 10-9) = 598,7 • 10-6 μm = 0,59 • 10-9 m
5,2 • 10-3
2. λ = yd
L
Lλ = yd
d = Lλ
y
d = (4,92)(632,8 • 10-9) = 1638,6 • 10-7 = 16,38 • 10-9 m
1.9 • 10-2
3. y = 2λ
W
Wy = 2λ
W = 2λ
y
W = 2(632,8 • 10-9) = 486,8 • 10-7 = 4,87 • 10-9 m
2,6 • 10-2
Esperimento di Young
Nel 1801 Thomas Young (1773-1829) effettuò un'esperienza decisiva a favore dell'ipotesi
ondulatoria della luce, mostrando che anche con i raggi luminosi si possono verificare i
fenomeni di interferenza e diffrazione, tipici dei fenomeni ondulatori
Un raggio di luce laser monocromatico colpisce un microscopico forellino e da questo, in
base al principio di Huygens, viene diffratto sulle due sottilissime fenditure S1 ed S2
equidistanti dalla fenditura singola.
Proseguendo, la luce colpisce uno schermo sul quale si visualizza una figura di interferenza
caratterizzata da bande chiare e scure, cioè da antinodi in cui l'interferenza è costruttiva
e da nodi in cui l'interferenza è distruttiva.
L'esperimento di Young permette di ricavare anche, misurando la distanza tra le bande e
la distanza dello schermo, di misurare la lunghezza d'onda della luce che è dell'ordine dei
10-7 m
Una relazione approssimata per determinare la lunghezza d'onda λ è la seguente:
λ = dy / L
dove d è la distanza tra le fenditure, y è la distanza tra due massimi consecutivi e L la
distanza dello schermo dalla doppia fenditura.
La relazione è valida per L >> d
L'esperimento della doppia fenditura ebbe un'importanza storica decisiva perchè pose
un punto fermo alla annosa questione della natura della luce, stabilendone la natura
ondulatoria.
LA DIFFRAZIONE
Una delle proprietà più curiose delle onde elettromagnetiche – e comune
a tutti i fenomeni ondulatori – è la loro capacità di "aggirare gli ostacoli".
La luce che attraversa una fenditura non si propaga solo "in avanti", come
farebbe un corpuscolo materiale, ma tende a espandersi nello spazio,
coprendo una regione ben più grande della fenditura attraverso la quale è
passata. Questo fenomeno prende il nome di diffrazione, e si manifesta
quando le dimensioni degli ostacoli che l'onda incontra risultano
paragonabili alla sua lunghezza d'onda. In maniera analoga, se la luce
incontra un ostacolo sufficientemente piccolo, non si crea una zona
d'ombra netta dietro a esso, perché la luce tende a "richiudersi" per
ripristinare il fronte d'onda originario.