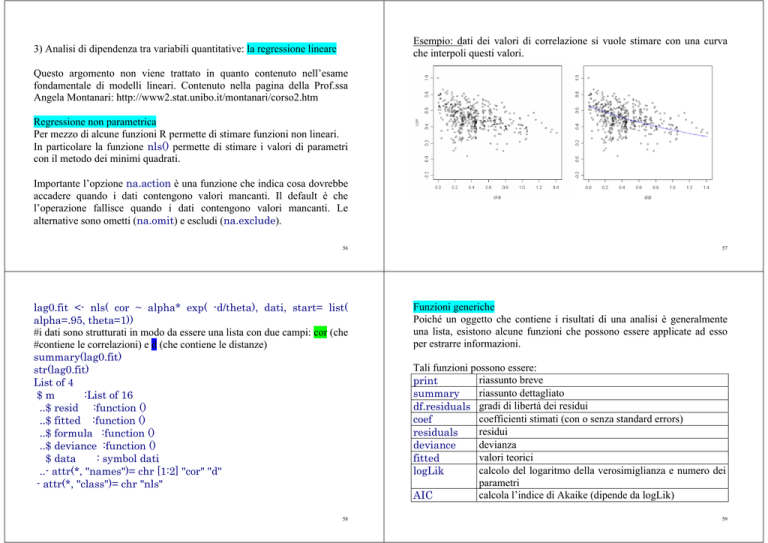
Esempio: dati dei valori di correlazione si vuole stimare con una curva
che interpoli questi valori.
3) Analisi di dipendenza tra variabili quantitative: la regressione lineare
Questo argomento non viene trattato in quanto contenuto nell’esame
fondamentale di modelli lineari. Contenuto nella pagina della Prof.ssa
Angela Montanari: http://www2.stat.unibo.it/montanari/corso2.htm
Regressione non parametrica
Per mezzo di alcune funzioni R permette di stimare funzioni non lineari.
In particolare la funzione nls() permette di stimare i valori di parametri
con il metodo dei minimi quadrati.
Importante l’opzione na.action è una funzione che indica cosa dovrebbe
accadere quando i dati contengono valori mancanti. Il default è che
l’operazione fallisce quando i dati contengono valori mancanti. Le
alternative sono ometti (na.omit) e escludi (na.exclude).
56
57
lag0.fit <- nls( cor ~ alpha* exp( -d/theta), dati, start= list(
alpha=.95, theta=1))
#i dati sono strutturati in modo da essere una lista con due campi: cor (che
#contiene le correlazioni) e d (che contiene le distanze)
summary(lag0.fit)
str(lag0.fit)
List of 4
$m
:List of 16
..$ resid :function ()
..$ fitted :function ()
..$ formula :function ()
..$ deviance :function ()
$ data
: symbol dati
..- attr(*, "names")= chr [1:2] "cor" "d"
- attr(*, "class")= chr "nls"
Funzioni generiche
Poiché un oggetto che contiene i risultati di una analisi è generalmente
una lista, esistono alcune funzioni che possono essere applicate ad esso
per estrarre informazioni.
58
59
Tali funzioni possono essere:
riassunto breve
print
riassunto dettagliato
summary
df.residuals gradi di libertà dei residui
coefficienti stimati (con o senza standard errors)
coef
residui
residuals
devianza
deviance
valori teorici
fitted
calcolo del logaritmo della verosimiglianza e numero dei
logLik
parametri
calcola l’indice di Akaike (dipende da logLik)
AIC
RAPPRESENTAZIONE
STATISTICHE
ANALITICA
DELLE
DISTRIBUZIONI
Si indica con f(x,θ) tale funzione, dove θ è il vettore dei parametri da
stimare sulla base dei dati disponibili.
Analisi statistica per verificare se i dati siano conformi ad un certo
modello teorico.
Gli scopi della rappresentazione analitica possono essere:
a) descrittivi: perequazione di dati, interpolazione di dati mancanti, etc.;
b) investigativi: rientrano nel campo della statistica inferenziale; in
particolare, si va alla ricerca di un modello teorico partendo da un
campione di osservazioni.
Tra questi tipi di analisi possiamo trovare la rappresentazione analitica
delle distribuzioni teoriche (distribution fitting), che consiste nel trovare
una funzione matematica interpolante che rappresenti adeguatamente un
fenomeno statistico osservato.
Data una serie di osservazioni di un carattere quantitativo, si suppone che
questi costituiscano un campione di una popolazione non nota a priori,
provengono da una determinata popolazione caratterizzata da una
funzione di densità di frequenza della quale si conosce l’espressione in
termini analitici.
60
RAPPRESENTAZIONE GRAFICA
Primo approccio esplorativo: grafico ad istogramma.
Es. Si generano 100 punti da una distribuzione normale di media 5 e sd
pari a 1.5.
>x.norm<-rnorm(100,mean=5,sd=1.5)
>hist(x.norm, main=”Istogramma dei dati osservati”)
62
Nella rappresentazione analitica possiamo individuare 4 fasi:
1) scelta del modello che si adatta meglio alle caratteristiche della
distribuzione dei dati;
2) stima dei parametri del modello scelto;
3) calcolo del grado di accostamento delle frequenze osservate rispetto a
quelle ottenute con il modello teorico;
4) applicazione di test statistici per saggiare la bontà del modello
(goodness of fit) in una logica inferenziale (importante se la finalità è b).
61
L’alternativa grafica è quella di utilizzare la funzione density() e di
stampare il grafico con l’istruzione generica plot()
>plot(density(x.norm), main=”stima densità di frequenza dei
dati osservati”)
63
Per mezzo di queste rappresentazioni grafiche ci si può già rendere conto
quale modello teorico meglio si adatti ai nostri dati.
Altro strumento grafico che si può utilizzare è il QQplot: qqnorm(),
qqplot() o qqline(),
R inoltre permette di calcolare la funzione di ripartizione empirica dei dati
tramite il comando ecdf()- empirical cumulative distribution function
plot(ecdf(x.norm),main=”Funzione di ripartizione empirica”)
z.norm<-(x.norm-mean(x.norm))/sd(x.norm)
qqnorm(z.norm)
abline(0,1)
In alternativa la funzione qqplot richiede il modello teorico di riferimento
come argomento.
64
SCELTA DEL TIPO DI FUNZIONE
Un metodo obiettivo per scegliere il tipo di curva teorica da usare nella
rappresentazione analitica è il criterio K di Pearson.
Famiglia di funzioni molto generale atta a rappresentare quasi tutte le
distribuzioni empiriche. Tali curve dipendono esclusivamente da 4
caratteristiche: media, variabilità, asimmetria e curtosi.
Standardizzando la distribuzione, il tipo di curva dipende solo dalla
misura di asimmetria e da quella di curtosi sintetizzate nel criterio K:
65
DISTRIBUZIONI PER VARIABILI DISCRETE
• Variabile casuale Binomiale (numero di successi in n prove)
>x<-rbinom(100,size=10,0.7)
(come si manifesta-> provare a fare un grafico con plot(table(x)))
• Variabile casuale Geometrica (tempo di attesa per avere il primo
successo)
> k<-0:15
> p.geo<-dgeom(k,1/8)
> plot(k, p.geo, type="h")
• Variabile casuale Poisson (variabile di conteggio: quanti eventi - tutti
uguali, indipendenti e equiprobabili - si manifestano in un intervallo
finito di tempo)
>k<-0:20
>p.pois<-dpois(k, lambda=5)
>plot(k, p.pois, type=”h”)
dove:
γ1: indice di asimmetria
γ2: indice di curtosi
66
67












