LABORATORIO DI MATEMATICA: COORDINATE POLARI
ESTENSIONE DELLE FUNZIONI TRIGONOMETRICHE
Uno strumento, che ci suggerisce come ampliare le nostre conoscenze, è il radar, strumento
fondamentale nella navigazione marittima e aerea.
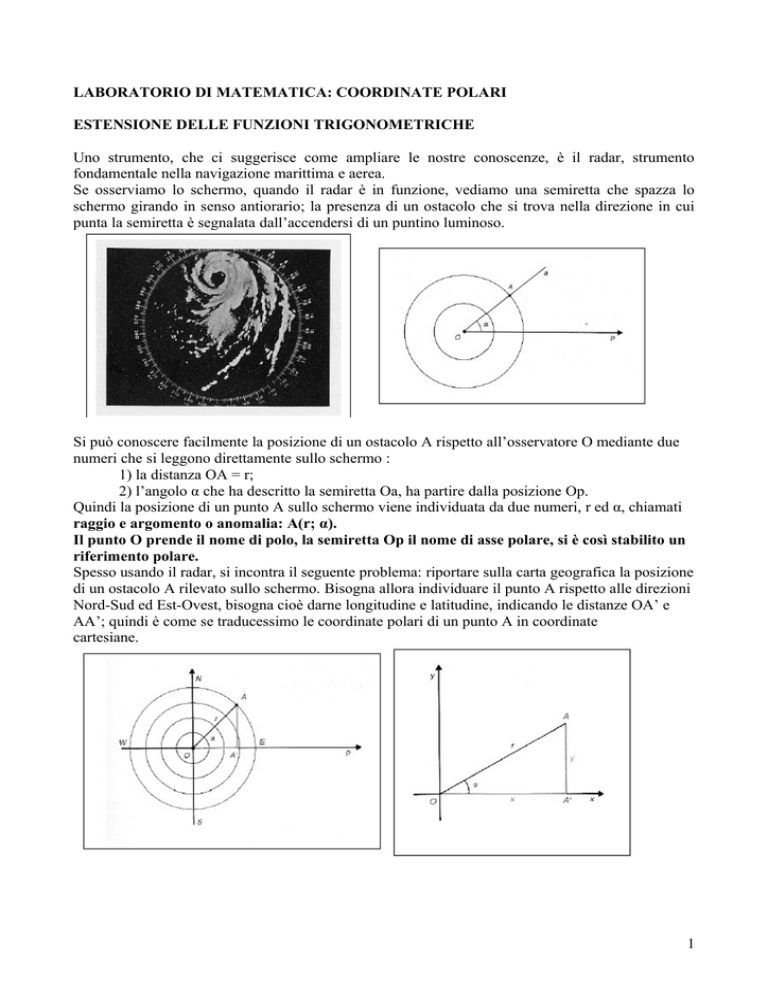
Se osserviamo lo schermo, quando il radar è in funzione, vediamo una semiretta che spazza lo
schermo girando in senso antiorario; la presenza di un ostacolo che si trova nella direzione in cui
punta la semiretta è segnalata dall’accendersi di un puntino luminoso.
Si può conoscere facilmente la posizione di un ostacolo A rispetto all’osservatore O mediante due
numeri che si leggono direttamente sullo schermo :
1) la distanza OA = r;
2) l’angolo α che ha descritto la semiretta Oa, ha partire dalla posizione Op.
Quindi la posizione di un punto A sullo schermo viene individuata da due numeri, r ed α, chiamati
raggio e argomento o anomalia: A(r; α).
Il punto O prende il nome di polo, la semiretta Op il nome di asse polare, si è così stabilito un
riferimento polare.
Spesso usando il radar, si incontra il seguente problema: riportare sulla carta geografica la posizione
di un ostacolo A rilevato sullo schermo. Bisogna allora individuare il punto A rispetto alle direzioni
Nord-Sud ed Est-Ovest, bisogna cioè darne longitudine e latitudine, indicando le distanze OA’ e
AA’; quindi è come se traducessimo le coordinate polari di un punto A in coordinate
cartesiane.
1
DALLE COORDINATE POLARI ALLE COORDINATE CARTESIANE
Fissando un riferimento cartesiano con l‘asse delle x coincidente con Op ed osservando il triangolo
OAA’, si può scrivere:
x = r cos α
y = r sin α
Affinchè ci sia corrispondenza biunivoca tra le coordinate polari e quelle cartesiane si suppone che
−π <α ≤π
DALLE COORDINATE CARTESIANE ALLE COORDINATE POLARI
Si conoscono le coordinate cartesiane del punto P=(x,y). Essendo il raggio la lunghezza del
segmento OP avremo che r = x 2 + y 2 . Per determinare l’ampiezza dell’angolo α osserviamo che:
π
- Se x=0 e y>0 allora α =
2
π
- Se x=0 e y<0 allora α = −
2
y
- Se x ≠ 0 allora = tan α
x
In realtà nell’intervallo − π < α ≤ π ci sono sempre due angoli la cui tangente ha come valore
y
,
x
perciò a seconda del quadrante in cui si trova il punto P si hanno i seguenti valori dell’angolo:
-
y
se x>0 α = arctan
x
y
se x<0 e y ≥ 0 α = arctan + π
x
y
se x<0 e y<0 α = arctan − π
x
Esempio 1. Determinare le coordinate polari del punto P=(6,3)
P è situato nel primo quadrante, quindi r =
6 2 + 32 =
45 = 3 5 α = arctan
3
≅ 0.46radianti
6
Esempio 2. Determinare le coordinate polari del punto P=(-4,4)
P è situato nel secondo quadrante, quindi r = 16 + 16 = 4 2
−π
3
4
α = arctan
+ π = π radianti
+ π ≅
4
4
− 4
2
DESCRIZIONE DI “OGGETTI GEOMETRICI” IN COORDINATE POLARI
Esercizio 1: determinare l’equazione della circonferenza di centro l’origine e raggio 3, sia in
coordinate cartesiane sia in coordinate polari.
In coordinate cartesiane: x 2 + y 2 = 9 . In coordinate polari i punti della circonferenza hanno lo
stesso valore del modulo uguale a 3, mentre l’angolo α può assumere qualsiasi valore. Quindi
l’equazione della circonferenza è r = 3 . Disegnare la circonferenza in coordinate polari utilizzando
Derive.
Esercizio 2: Qual è la curva che, in coordinate polari ha equazione α =
π
? Quale sarebbe la
4
corrispondente equazione in coordinate cartesiane?
π
mantengono lo stesso argomento mentre il
4
modulo varia assumendo valori non negativi via via crescenti
Suggerimento: i punti della curva di equazione α =
Osservazione: in coordinate cartesiane è naturale considerare i due sistemi di rette che formano il
“quadrettato di base” che fa da sfondo al riferimento. Sono le rette di equazioni x = h e y = k
3
In coordinate polari è invece naturale considerare altri due sistemi di curve che fanno da sfondo al
riferimento; sono le curve di equazione r = h α = k
Esercizio 3: Disegnare la curva che ha, in coordinate polari, l’equazione di primo grado α = 2r
Suggerimento: Completa la seguente tabella e riportala nel “piano polare”.
Punti
O
A
B
C
D
E
F
G
r
0
π /8
3π / 16
π /4
3π / 8
π /2
3π / 4
π
α
0
π /4
3π / 8
π /2
3π / 4
π
3π / 2
2π
Congiungendo i punti con opportuni tratti curvilinei, si osserva che la curva assume la forma di un
spirale.
4
Esercizio 4. Nel monito di un radar,due oggetti sono stati avvistati nelle posizioni A = (10,30° ) e
B = (5,60° ) , quanto distano i due oggetti tra di loro?
Suggerimento: supponiamo che i due punti siano disposti come in figura
Considerando il triangolo rettangolo OBQ si ha che BQ=…….., AQ=……… da cui AB=………
Esercizi:
1) Disegna le seguenti circonferenze r = 6 cos(α ) r = cos α .
1
.
α
Scrivi le equazioni in coordinate polari di: a) la circonferenza di centro nel polo O e raggio
3; b) la semiretta di origine O che forma un angolo α con l’asse polare; c) una retta
parallela all’asse polare e distante 3 da essa d) una retta perpendicolare all’asse polare e
distante 3 dal polo.
Ricordando le relazioni tra coordinate cartesiane e coordinate polari, riscrivi in coordinate
polari le relazioni espresse in coordinate cartesiane e viceversa: a) x 2 − y 2 = 9 ; b) xy = 5 ;
c) x 2 + y 2 − 4 x = 0 ; e) r 2 sin 2α = 1 ;f) r 2 cos 2α = 1 .
Calcola in riferimento polare la distanza tra A e B ( applica il teorema del coseno):
π
A = (1, ) B = (3,0)
2
Il un sistema di riferimento polare le seguenti curve scegliendo opportuni valori di α tra 0 e
2π costruendo la tabella dei valori corrispondenti di r e α : r = 1+ sin α ( curva detta
cardioide), r = 2 sin(2α ) ( quadrifoglio).
2) Disegna in coordinate polari il grafico delle seguenti funzioni: r = 2α , α = 2r , r =
3)
4)
5)
6)
5










