Statistica descrittiva

Statistica economica
a.a. 2013/14
Dr. L.Secondi
00A. Richiami di statistica descrittiva
Indicatori sintetici
Gli aspetti più importanti di una distribuzione di frequenza riguardano:
1.
La posizione
INDICI STATISTICI DI POSIZIONE
(MODA, MEDIANA,MEDIE)
SCOPO: SINTETIZZARE in un singolo valore
numerico l’intera distribuzione di frequenza per
effettuare confronti nel tempo, nello spazio
o tra circostanze differenti.
2.
La variabilità
INDICI STATISTICI DI VARIABILITA’
SCOPO: misurare L’ATTITUDINE di un fenomeno
ad assumere differenti modalità
3.
La forma
INDICI DI ASIMMETRIA
SCOPO: misurare la SIMMETRIA di una distribuzione
rispetto ad un punto notevole
(es.: rispetto ad una misura di posizione)
2
Il caso di studio
Un’azienda internazionale che produce e vende abbigliamento
tendenza giovane (donna, uomo, bambino, accessori) è presente già
nel Lazio e decide di espandere la propria attività aprendo nuovi punti
vendita in altre città italiane
Per tale espansione l’azienda ha bisogno del finanziamento da parte
di una banca per acquisti di immobili (nuove sedi) e di attrezzature
I manager dell’azienda devono predisporre dei documenti da
fornire alla banca
Servono quindi dei DATI che assicurino la banca sullo stato di
salute dell’azienda
Si hanno a disposizione i dati di bilancio (più altre specifiche
informazioni) dei punti vendita già operativi nel Lazio.
Queste informazioni comprendono:
ricavi e costi, numero di addetti, ubicazione del punto vendita,
informazioni sul responsabile del punto vendita, se il punto
vendita effettua vendite on-line
3
Matrice dei dati
Punti
vendita
Ricavi
Costi
addetti
ubicazione
Genere
respons.
Vendita R.O
On-line
1
350
205
5
centro
maschio
si
145
2
200
100
3
periferia
maschio
si
100
3
600
350
10
semicentro
femmina
no
250
4
500
270
10
periferia
femmina
no
230
5
270
200
6
centro
maschio
no
70
6
180
120
3
centro
maschio
no
60
7
205
105
3
periferia
maschio
no
100
8
340
210
5
semicentro
femmina
no
120
9
280
140
4
centro
femmina
si
140
4
Tendenza centrale: la media
• Il modo più intuitivo per sintetizzare un insieme di
valori passa attraverso il calcolo della media
• Media (aritmetica) = punto di equilibrio o baricentro
dell’insieme di valori
• È una media analitica, funzione di tutti i valori
• La media aritmetica risente fortemente dei valori
estremi
Dati n valori osservati x1, x2,…, xn di un carattere
quantitativo X
1
1 n
x a = (x 1 + x 2 + ... + x n ) = ∑ x i
n
n i =1
Media di una distribuzione di
frequenza
Impossibile v isualizzare l'immagine.
Addetti
(valori xj)
Numero punti
vendita
(frequenze nj)
xj*nj
3
2
3*2=6
4
1
4*1=4
6
3
6*3=18
7
1
7*1=7
10
2
10*2=20
Impossibile v isualizzare l'immagine.
K
K
nj
∑
j=1
K
∑x
Media
xa =
x j ⋅ nj = 55
∑
j=1
=n=9
K
j
j=1
K
∑x
⋅ nj
∑ nj
=
j
j=1
n
⋅ nj
55
=
= 6,11
9
6 è il numero
complessivo di
addetti nei primi 3
punti vendita
18 è il numero
complessivo di
addetti nei 2 punti
vendita in ciascuno
dei quali lavorano 6
addetti
55 è il numero
complessivo di addetti
(l’intensità totale del
carattere)
j=1
6
Media di una distribuzione di
frequenza con classi di valori
Classi di
superficie
(in ettari)
Numero
aziende
cj*nj
(nj)
Valore
centrale
classi (cj)
0-1
120
0,5
60
1-2
160
1,5
240
2-3
220
2,5
550
3-5
212
4
848
5-10
205
7,5
1537,5
10-20
110
15
1650
20-40
65
30
1950
40-80
21
60
1260
Impossibile v isualizzare l'immagine.
K
n=
nj
∑
j=1
K
xa ≈
c jn j
∑
j=1
=
n
8095,5
=
= 7,27
1113
La superficie
media di una
azienda agricola
è di 7,27 ettari
K
= 1113
c jn j
∑
j=1
= 8095,5
Fonte: Borra-Di Ciaccio, pag. 71
7
Mediana
• È il valore che occupa la posizione
centrale nell’insieme ordinato di tutti i
valori x = x( ) ≤ x( ) ≤ ... ≤ x( ) = x
min
1
Tra x(1) e Me è
contenuto il 50%
dei valori
X(1)
2
n
max
Tra Me e x(n) è
contenuto il restante
50% dei valori
Me
X(n)
• È una media di posizione
8
Come individuare la posizione
centrale o rango della mediana
• Insieme di n valori
la posizione centrale è data da (n + 1)
• n dispari
2
Me = x  n+1 


 2 
• n pari
le posizioni centrali sono due, n e n + 1
2
2
x n  ≤ Me ≤ x n

 +1 
2 
 
2
Di solito
x n  + x n
Me =

 +1 
2 
 
2
2
9
Calcolo della mediana
• In un insieme di 9 valori, la posizione
centrale è la quinta. Il termine che occupa
la quinta posizione è la mediana
100
200
XXX
300
X
XX
400
500
600
X
X
700
Elimino ogni volta
l’osservazione più
piccola e quella
più grande
Mediana = 280,
cioè il valore che occupa la quinta posizione
10
Calcolo della mediana
Se il valore estremo fosse 800 invece di 600
la mediana resterebbe invariata
100
200
XXX
300
X
XX
400
500
600
700
X
800
X
Mediana = 280
La mediana non è influenzata dalla presenza di valori estremi
Fornisce una misura della tendenza centrale migliore rispetto alla
media quando ci sono alcune osservazioni molto grandi o molto
piccole
11
Mediana da una distribuzione di
frequenza (con le freq. rel. cum.)
Addetti
(xj)
Numero
punti vendita
(nj)
Frequenze
cumulate
Nj
Frequenze
rel cum.
Fj
3
2
2
0,22
4
1
3
0,33
6
3
6
0,67
7
1
7
0,78
10
2
9
1,00
Sulla colonna delle frequenze relative cumulate si
individua la prima Fj che è uguale o maggiore di 0,5
Il corrispondente valore xj è la mediana della distribuzione
Me=6
12
Mediana di una distribuzione di
frequenza con classi di valori
Classi di
superficie
(in ettari)
Numero
Freq.
aziende cumulate
(Nj)
(nj)
0-1
120
120
1-2
160
280
2-3
220
500
3-5
212
712
5-10
205
917
10-20
110
1027
20-40
65
1092
Oltre 40
21
1113
rango mediana =
n+1
=
2
1113 + 1
=
= 557
2
L’elemento che occupa
la posizione 557
è uno dei 212 valori
della classe 3-5
La mediana è
contenuta nella
classe 3-5
13
Mediana di una distribuzione di
frequenza con classi di valori
Classi di
superficie
(in ettari)
Numero
aziende
Freq.
cum.
Freq. rel.
cum.
(nj)
(Nj)
(Fj)
0-1
120
120
0,108
1-2
160
280
0,252
2-3
220
500
0,449
3-5
212
712
0,640
5-10
205
917
0,824
10-20
110
1027
0,923
20-40
65
1092
0,981
Oltre 40
21
1113
1,000
Im=estr inf della classe
mediana=3
Fm-1=freq rel cum fino
alla classe precedente a
quella mediana =0,449
Fm=freq rel cum
fino alla classe
mediana=0,640
∆m=ampiezza della
classe mediana=
=5-3=2
 0,5 − Fm−1 
 0,5 − 0,449 
Me ≈ Im + 
∆ m = 3 + 
2 = 3,53
 0,640 − 0,449 
 Fm − Fm−1 
14
Quartili
• Sono 3 indici di posizione, Q1 Q2 e Q3
xmin = x (1) ≤ x (2 ) ≤ ... ≤ x (n ) = xmax
Tra x(1) e Q1 è
contenuto il 25% dei
valori (più bassi)
X(1)
Tra Q1 e Q2 è
contenuto il 25%
dei valori
Q1
Tra Q3 e x(n) è
contenuto il 25% dei
valori (i più alti)
Q2=Me
Q3
X(n)
Tra Q2 e Q3 è
contenuto il
25% dei valori
15
Percentili
Sono quei valori che dividono la distribuzione in
cento parti di uguale numerosità
Mediana=50-esimo percentile
Q3= 75-esimo percentile
P10 = decimo percentile: lascia alla sua sinistra il
10% dei valori
P90 = novantesimo percentile: lascia alla sua
destra il 10% dei valori
16
Moda
• È la modalità più frequente
• In un insieme di valori: quel termine che si ripete più volte
• In una distribuzione di frequenza: quella modalità che ha la
frequenza più alta
• In una distribuzione di frequenza con classi di valori: ogni
valore della classe con la più alta densità di frequenza
• Può non esistere
• Può non essere unica
• Può essere una modalità “poco rappresentativa” del fenomeno
• Per chi vende abbigliamento, la moda rappresenta un
parametro utile per decidere in merito a come rifornire il
negozio: saranno ordinati più capi delle taglie più diffuse
17
Variabilità
• Il calcolo di una media non esaurisce la
descrizione sintetica di un fenomeno
osservato in un collettivo
• Due insiemi di valori o due distribuzioni di
frequenza, pur avendo lo stesso valore
medio, possono essere molto differenti tra
di loro
• Gli indici di variabilità forniscono
informazioni complementari a quelle degli
indici medi
18
• VARIABILITA’: attitudine di un carattere
ad assumere diverse modalità
Varianza (σ2);
Indici di variabilità
Deviazione standard (σ);
Coefficiente di variazione (CV);
- Un indice di variabilità deve assumere il valore minimo se e solo se tutte
le unità della distribuzione presentano uguale modalità del carattere;
- Un indice di variabilità deve aumentare all’aumentare della diversità tra le
modalità assunte dalle varie unità;
19
La variabilità (distribuzioni teoriche)
unità
1
2
3
4
5
Reddito Reddito Reddito
A (000) B (000) C (000)
40
20
100
15
20
0
10
20
0
30
20
0
5
20
0
100
100
100
X A = X B = X C = 20
20
Esempio – Si considerino la due seguenti distribuzioni relative a due collettivi di individui,
rispettivamente residenti nella città X e Y, classificati in base alla loro misura di scarpa. Determinare
i valori medi delle due distribuzioni.
Individui residenti nella città X
Individui residenti nella città Y
Misura di
scarpa
ni
Misura di
scarpa
ni
38
0
38
20
39
50
39
10
40
0
40
20
Tot.
50
Tot.
50
39 ⋅ 50
µX =
= 39
50
(38 ⋅ 20) + (39 ⋅10) + (40 ⋅ 20)
µy =
= 39
20 + 10 + 20
21
Misure di variabilità come
ampiezza di un intervallo
Il range (o campo di variazione) range = x − x
è l’ampiezza dell’intervallo che contiene tutti i
valori
max
min
La differenza interquartile dQ = Q3 − Q1
è l’ampiezza dell’intervallo che contiene il
50% dei valori (quelli centrali)
La variabilità aumenta al crescere di questi
indici
22
Misure di variabilità come dispersione dalla media
La varianza σ2 è funzione delle differenze (scarti) tra ogni
valore xi e la media x
1 n
2
σ = ∑ (xi − x )
n 1=1
2
σ2 ≥ 0
n
La devianza è il numeratore della varianza Dev(X) =
2
(
x
−
x
)
∑ i
i=1
La deviazione standard (o scarto quadratico medio) è la
radice quadrata della varianza
1 n
2
σ =
(
x
−
x
)
∑ i
n i=1
Il coefficiente di variazione CV è il rapporto tra la dev.
standard e la media moltiplicato per 100
CV =
σ
x
100
x>0
23
Variabilità
Ricavi
xj
350
Scarti
dalla
media
(xj-µ)
25
Quadrato
degli
scarti
(xj-µ)2
625
200
-125
15.625
600
275
75.625
500
175
30.625
270
-55
3.025
180
-145
21.025
205
-120
14.400
340
15
225
280
-45
2.025
0
163.200
media µ = x = 325
n
∑ (xi − x ) = 0
i=1
Per la proprietà
della media
n
2
(
x
−
x
)
∑ i
= Dev(X) = 163200
i=1
Devianza=163200
1 n
Dev(X)
2
2
(
)
x
−
x
=
=
σ
=
∑
i
n
n i=1
163200
=
= 18133,3
9
Varianza=18133,3
1 n
2
(
)
x
−
x
=
σ =
∑
i
n i=1
Dev.std.=134,7
24
= 18133,3 = 134,7
24
Varianza di una distribuzione di
frequenza
Addetti
(xj)
Numero
punti vendita
3
2
19,34
4
1
4,45
6
3
0,04
7
1
0,79
10
2
30,26
totale
9
(nj)
(xj-µ)2*nj
µ = x = 6,11
1 K
54,88
2
σ = ∑ (x j − x ) n j =
= 6,10
n j=1
9
2,47
CV =
100 = 40,43%
σ = 6,10 = 2,47
6,11
2
25
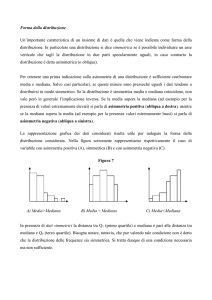
Forma di una distribuzione
Asimmetria: studiare l’asimmetria di una distribuzione significa
studiarne un particolare aspetto della forma. Una distribuzione si
dice asimmetrica se non è possibile individuare un asse verticale
che tagli la distribuzione in due parti specularmente uguali. Il
concetto di simmetria è applicabile solo a caratteri ordinabili
Un modo intuitivo per studiare l’asimmetria di una distribuzione è quello che si
basa sulle relazioni esistenti tra media aritmetica, mediana e moda in
distribuzioni unimodali
26
Simmetria
30
25
20
15
10
5
0
1
2
3
4
5
6
7
8
9
10
11
12
13
media = mediana = moda
Asimmetria negativa
Asimmetria positiva
60
60
50
50
40
40
30
30
20
20
10
10
0
0
1
1
2
3
4
5
6
7
8
9
10
11
media > mediana ≥ mod a
12
2
3
4
5
6
7
8
9
10
11
12
13
13
media < mediana ≤ mod a
27
Indice di asimmetria
Indice di Fisher: È funzione
aritmetica elevati al cubo
1
β=
nσ3
n
∑ (x i
i =1
3
− x)
Attenzione: la nullità degli indici di asimmetria è
condizione necessaria ma non sufficiente per poter
affermare che la distribuzione è simmetrica.
degli
1
β=
nσ 3
scostamenti
K
∑ (x
− x ) nj
3
j
j=1
dalla
media
per una distrib. di
freq.
Se la distribuzione è simmetrica β=0 (non vale il contrario)
β >0
asimmetria positiva
β <0
asimmetria negativa
Un secondo indice è espresso da:
ed è l’indice di “Skewness” (asimmetria) di Pearson.
Un altro indice di asimmetria molto diffuso è dato
da:
sk =
s1 =
m − Mo
σ
m − Me
σ
28
Qual è la forma della distribuzione dei Ricavi
nei 9 punti vendita considerati?
Punti
vendita
Ricavi
Scarti
Scarti al cubo
3
( xi − x )
1
350
25
15,625
2
200
-125
-1,953,125
3
600
275
20,796,875
x = 325
1
M3 =
n
=
4
500
175
5,359,375
5
270
-55
-166,375
6
180
-145
-3,048,625
7
205
-120
-1,728,000
8
340
15
3,375
9
280
-45
-91,125
Me = 280
n
∑ (x
i
σ = 134, 6
3
− x)
i =1
19,188, 000
= 2.132.000
9
2.132.000
β =
= 0, 87
2.441.836
29
Calcolo dell’indice di asimmetria
Indice
asimm.
β
s1
Ricavi
0,87
0,33
Utilizzando i due
indici si conclude
che la distribuzione
presenta una
asimmetria positiva
30