potenze.notebook
February 15, 2014
Come vedremo risultano fondamentali in tanti ambiti: in economia, in ogni fenomeno naturale che prevede lo studio di una intensità (suoni, terremoti...), nella datazione di reperti archeologici, nei modelli di crescita. Partiamo con un ripasso:
Siano a e n numeri naturali diversi da zero. Si definisce potenza di base a ed esponente n il prodotto di tanti fattori tutti uguali ad a, quanti ne indica l'esponente.
Siano a e n numeri interi diversi da zero. Se la base è un numero negativo, la potenza si definisce in modo analogo alla precedente. Se l'esponente è negativo, la potenza è il prodotto di tanti fattori, quanti ne indica l'esponente considerato con il segno positivo, tutti uguali al reciproco della base:
potenze.notebook
February 15, 2014
Siano a e n numeri razionali diversi da zero. Significa che a e n possono scriversi come frazioni. Si pone:
Se n è pari, il radicando deve essere positivo.
Siano a e n numeri reali diversi da zero. Che significato ha la potenza n­essima di a?
E' necessario ricordare la definizione di numero reale:
Un numero reale è l'elemento separatore di due classi contigue di numeri razionali.
Due classi (o insiemi) A e B non vuote di numeri reali si dicono contigue se
­ sono separate, cioè ogni elemento della classe A è minore di ogni elemento della classe B;
­ godono della proprietà dell’avvicinamento indefinito: scelto ad arbitrio un numero positivo ε piccolo a piacere, esiste sempre un elemento della seconda classe e uno della prima la cui differenza sia inferiore ad ε.
potenze.notebook
Ad esempio l'insieme dei numeri minori di 2 e l'insieme dei numeri maggiori di 2 costituiscono due classi contigue, mentre l'insieme dei numeri minori di 3 e l'insieme dei numeri maggiori di 4 non lo sono. Nonostante la prima condizione sia verificata per entrambi gli esempi, cioè sia i primi due insiemi che i secondi due sono esempi di classi separate, tuttavia scelto ad esempio ε=0.01, nel primo caso troviamo due numeri la cui differenza sia minore di 0.01, ne secondo caso non è possibile, perché la differenza tra un numero più grande di 4 e uno più piccolo di tre è sempre maggiore di 1, non può essere più piccola di 0.01.
February 15, 2014
potenze.notebook
February 15, 2014
Cerchiamo ad esempio di ricostruire due classi contigue che definiscono Poiché 2 è compreso tra 1 e 4, è compreso tra 1 e 2.
Dividiamo l'intervallo 1 e 2 in dieci parti uguali: 1,1 ­ 1,2 ­ 1,3 ­ .... 1,9. Di ognuno di questi numeri calcoliamo il quadrato: 1,21 ­ 1,44 ­ 1,69 ­ 1,96 ­ 2,25 ­..... Poiché 2 è compreso tra 1,96 e 2,25, avremo che radice di 2 è compreso tra la radice di 1,96 e la radice di 2,25:
potenze.notebook
February 15, 2014
Cerchiamo ad esempio di ricostruire due classi contigue che definiscono Ora dividiamo l'intervallo 1,4 ­ 1,5 in dieci parti uguali: 1,41 ­ 1,42 ­ 1,43 ­ ...... 1,49 e di questi numeri calcoliamo il quadrato: 1,9881 ­ 2,0164 ­ .....
Poiché 2 è compreso tra 1,9881 e 2,0164, radice di 2 sarà compreso tra la radice di 1,9881 e la radice di 2,0164:
Procedendo in questo modo troviamo due successioni: 1 ­ 1,4 ­ 1,41 ­ ..... e 2 ­ 1,5 ­ 1,42 ­... che approssimano rispettivamente per difetto e per eccesso radice di 2 e che costituiscono due classi contingue di numeri razionali di cui radice di due è l'elemento separatore.
Siamo pronti per definire la potenza a esponente reale di un numero reale: basta considerare le successioni di numeri che hanno come esponente gli elementi delle classi contigue che definiscono l'esponente:
potenze.notebook
February 15, 2014
sono alcuni termini della successione che si avvicina ad a elevato alla radice di 2 da sinistra e in modo analogo si determinano gli elementi più grandi di a elevato alla radice di 2.
potenze.notebook
February 15, 2014
Proprietà delle potenze:
assumiamo a e b diversi da zero:
non ha significato
con x numero reale non ha significato se a è negativo
Da ora in poi considereremo solo potenze in cui assumiamo che la base a sia maggiore di zero e diversa da 1.
potenze.notebook
Se abbiamo una equazione di questo tipo
February 15, 2014
riusciamo facilmente a risolverla
perché 8 è 2 elevato alla terza
Ma se invece abbiamo
dobbiamo aspettare qualche lezione prima di poterla risolvere. Invece se al membro destro e al membro sinistro abbiamo potenze di una stessa base, riusciamo a trovare subito la soluzione dell'equazione.
ESEMPIO
potenze.notebook
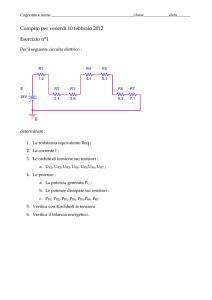
ESERCIZI
February 15, 2014
potenze.notebook
February 15, 2014
RISOLTO DA TUTTI....