Programmazione didattica - Dipartimento matematica- fisica (A047-A049)
I docenti di matematica e fisica, tenendo presente la riforma della scuola secondaria
superiore e, gli obiettivi richiesti dal decreto del ministero della Pubblica Istruzione del
22 agosto 2007, n. 139 riportano di seguito la loro programmazione didattica per l’a.s.
2012/2013.
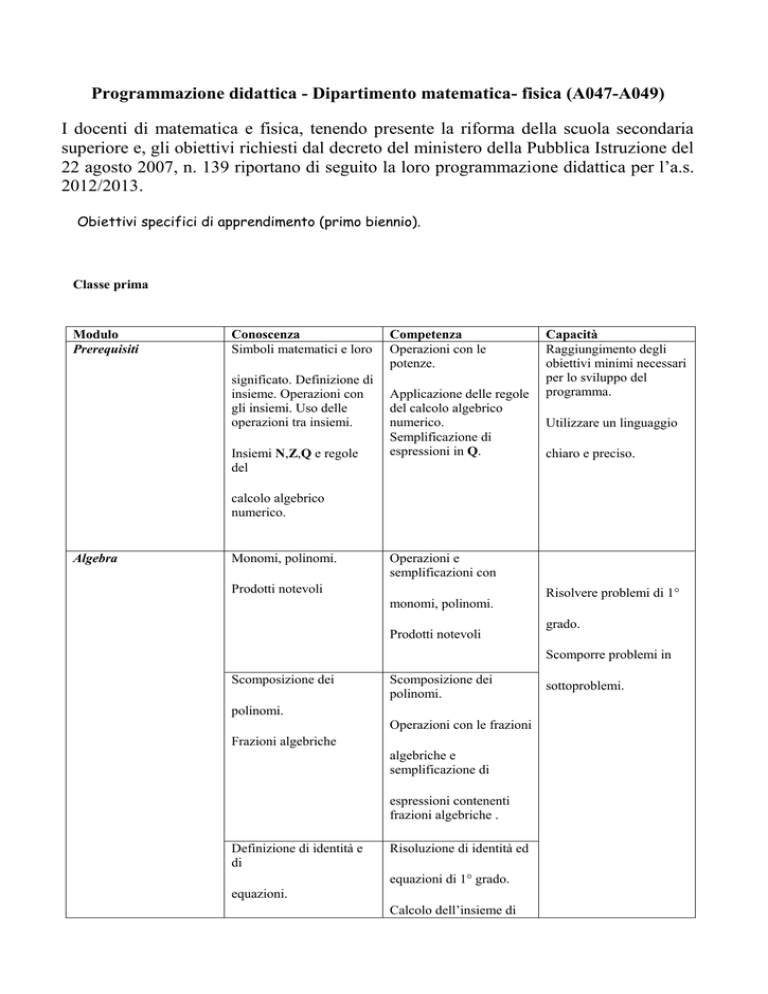
Obiettivi specifici di apprendimento (primo biennio).
Classe prima
Modulo
Prerequisiti
Conoscenza
Simboli matematici e loro
significato. Definizione di
insieme. Operazioni con
gli insiemi. Uso delle
operazioni tra insiemi.
Insiemi N,Z,Q e regole
del
Competenza
Operazioni con le
potenze.
Applicazione delle regole
del calcolo algebrico
numerico.
Semplificazione di
espressioni in Q.
Capacità
Raggiungimento degli
obiettivi minimi necessari
per lo sviluppo del
programma.
Utilizzare un linguaggio
chiaro e preciso.
calcolo algebrico
numerico.
Algebra
Monomi, polinomi.
Operazioni e
semplificazioni con
Prodotti notevoli
monomi, polinomi.
Prodotti notevoli
Risolvere problemi di 1°
grado.
Scomporre problemi in
Scomposizione dei
Scomposizione dei
polinomi.
polinomi.
Operazioni con le frazioni
Frazioni algebriche
algebriche e
semplificazione di
espressioni contenenti
frazioni algebriche .
Definizione di identità e
di
Risoluzione di identità ed
equazioni di 1° grado.
equazioni.
Calcolo dell’insieme di
sottoproblemi.
Principi di equivalenza
delle equazioni.
definizione di una
equazione fratta.
Risolvere problemi di 1°
Equazioni di 1° grado
intere e fratte.
Modulo
Geometria
grado.
Conoscenza
Struttura di un teorema
Competenza
Saper distinguere
ipotesi e tesi
Enti geometrici, assiomi
euclidei e teoremi
fondamentali.
Criteri di congruenza dei
triangoli.
Rette ortogonali.
Dimostrazione dei
teoremi riguardanti le
proprietà delle figure
piane studiate, in
particolare i triangoli.
Rette parallele
Relazioni fra gli
elementi di un triangolo.
Luoghi geometrici.
Simmetrie: assiale e
centrale.
Capacità
Acquisire capacità
logiche attraverso
l’applicazione corretta
del metodo assiomaticodeduttivo
Risolvere problemi
dimostrativi. Utilizzare
un linguaggio chiaro e
preciso. Comunicare in
modo formalmente
corretto.
Dimostrazione dei
teoremi sulle rette
parallele e
perpendicolari.
Classe seconda
Modulo
Algebra
Conoscenza
Principi delle
disuguaglianze.
Disequazioni intere, fratte,
sistemi di disequazioni.
Sistemi lineari. Metodi di
risoluzione.
Metodo delle coordinate.
Retta associata
all’equazione : y = ax + b
e sua rappresentazione.
Competenza
Risoluzione di
disequazioni di 1° grado e
di grado superiore
riconducibili ad esse.
Capacità
Sistemi di 1° grado
numerici e letterali.
Risolvere problemi con
sistemi di 1°grado.
Numeri irrazionali: radice
ennesima aritmetica e
algebrica.
L’insieme R
Operazioni con i radicali
Equazioni di 2° grado
incomplete e complete,
formula risolutiva.
Risoluzione di
Parabola associata
all’equazione : y = ax2 +
bx + c e sua
rappresentazione.
Disequazioni di 2° grado.
equazioni di 2° grado.
Risolvere i problemi
di 2° grado. Discutere
i limiti dell’incognita
di un problema.
Acquisire la capacità
di organizzare e di
collegare
gli
Risoluzione di
disequazioni di 2° grado e argomenti.
di grado superiore
riconducibili ad esse.
Equazioni binomie,
trinomie, biquadratiche,
irrazionali.
Risoluzione di equazioni
binomie, trinomie,
biquadratiche e
irrazionali. Condizioni di
accettabilità.
Sistemi di 2° grado.
Risoluzione di sistemi di
2° grado.
Ampliare le capacità
logiche di analisi e di
sintesi.
Intersezioni rette-coniche.
Circonferenza e cerchio.
Geometria
Punti notevoli di un
triangolo. Poligoni
inscritti e circoscritti.
Principali trasformazioni
geometriche. Traslazioni,
rotazioni.
Equivalenza di figure
piane .Teorema di
Pitagora e teoremi di
Euclide.
Classi di grandezze
omogenee, grandezze
commensurabili ed
incommensurabili.
Proporzionalità diretta e
inversa. Funzioni: y = hx ,
y = k/x .Teorema di
Talete. Similitudine,criteri
relativi
Dimostrazioni dei teoremi
relativi
Risolvere problemi
dimostrativi.
Utilizzare un
linguaggio chiaro e
preciso.
Comunicare in modo
formalmente corretto.
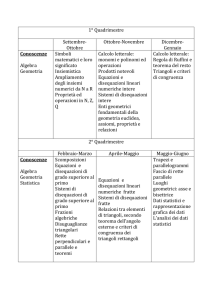
Scansioni Temporali
ANNO SCOLASTICO 2012 – 2013
Matematica -
Classe prima
I trimestre
Unità di
I
II
III
Settembre-Ottobre
Ottobre-Novembre
Dicembre
apprendimento
Periodo di
svolgimento
• Prerequisiti
• Algebra
• Geometria
• Elementi di
informatica
Simboli matematici e
loro significato.
Insiemistica.
Insiemi N,Z,Q e
regole
Calcolo letterale
Calcolo letterale.
Lo studio razionale
della geometria.
Triangoli
Assiomi e teoremi:
rette e angoli.
del calcolo algebrico
Algoritmi
numerico.
Obiettivi
fondamentali
Conoscere i simboli
Conoscere e saper
matematici e la loro
usare le regole del
• Conoscenze
Conoscere e saper usare
le
regole del calcolo
funzione.
• Competenze
calcolo letterale.
letterale.
Concetto di
• Capacità
corrispondenza
biunivoca.
Conoscere e saper
applicare le regole del
Conoscere i concetti
primitivi e gli
Conoscere e saper
assiomi
applicare i criteri di
della geometria euclidea.
congruenza dei
Familiarità con gli
strumenti
triangoli per la risoluzione dei
problemi sintetici.
informatici.
calcolo numerico
Contenuti
fondamentali
Conoscere le
strutture degli
algoritmi.
Insiemi numerici N,Z, Monomi. Polinomi.
Q.
Operazioni con
Proprietà ed
operazioni in N, Z, Q. polinomi. Prodotti
Uso delle operazioni
tra
Prodotti notevoli
Criteri di congruenza
dei triangoli.
notevoli.
Rette semipiani
insiemi.
angoli e strisce.
Algoritmi per la
risoluzione di
semplici problemi.
Verifiche
Almeno una prova
scritta per valutare le
capacità e le
conoscenze
acquisite.
Almeno una prova
scritta per valutare le
capacità e le
conoscenze acquisite.
Almeno una prova
scritta per valutare le
capacità e le
conoscenze acquisite.
Pentamestre
Unità di
I
II
III
apprendimento
Periodo di
svolgimento
Febbraio-Marzo
Aprile-Maggio
Maggio-Giugno
• Algebra
• Geometria
• Statistica
Calcolo letterale:
divisioni tra
polinomi
Scomposizioni.
Frazioni algebriche.
Equazioni di 1° grado
Equazioni di 1° grado Fratte.
intere e fratte.
Problemi di geometria di
Rette perpendicolari. Simmetrie.
1° grado.
Rette parallele.
Proprietà dei
Luoghi geometrici.
Poligoni: proprietà.
triangoli.
Parallelogrammi:
Dati e previsioni:
proprietà.
concetti
fondamentali.
Frequenze e tabelle.
Rappresentazioni
grafiche dei dati.
Obiettivi
fondamentali
• Conoscenze
• Competenze
• Capacità
Conoscere e saper Saper operare con le
usare le regole del frazioni.
calcolo letterale.
Saper risolvere le
equazioni di
Saper scomporre.
Conoscere e saper
applicare i teoremi
relativi alla teoria
dei criteri di
congruenza dei
triangoli e delle rette
perpendicolari.
Conoscere ed
applicare i teoremi
sulle rette
Parallele.
Contenuti
fondamentali
Divisioni tra
polinomi. Regola di
Ruffini e teorema
del resto.
Scomposizione dei
polinomi. Teoria
delle rette parallele.
Criteri di congruenza
dei triangoli
rettangoli.
Saper risolvere problemi
di geometria.
Saper risolvere problemi
1° grado numeriche e di 1° grado.
fratte.
Conoscere ed
applicare i teoremi sui
triangoli.
Conoscere e utilizzare
i luoghi geometrici.
Scomposizioni.
Frazioni
Equazioni.
Poligoni.
algebriche.
Parallelogrammi.
Equazioni di 1° grado
intere e fratte.
Trapezi.
criteri di congruenza dei
triangoli rettangoli.
L’indagine statistica, Luoghi geometrici.
caratteri e modalità.
Simmetria assiale,
simmetria centrale.
Frequenze e tabelle.
Rappresentazioni
grafiche dei dati.
Verifiche
Almeno una prova
scritta per valutare le
capacità e le
conoscenze acquisite
.
Almeno una prova
Almeno una prova scritta
scritta per valutare le per valutare le capacità e
capacità e le
le conoscenze acquisite.
conoscenze acquisite.
N.B. La scansione mensile è da ritenersi indicativa.
Nel mese di gennaio si effettueranno interventi di recupero
Classe seconda
I trimestre
Unità di
I
II
III
apprendimento
Periodo di
Settembre-Ottobre
Ottobre - Novembre
Dicembre
Equazioni di primo
grado letterali.
Disequazioni di primo
Radicali.
grado.
Equivalenza delle
Le isometrie.
figure piane.
svolgimento
Titolo
• algebra
Sistemi di primo grado.
• geometria
Circonferenza e
cerchio.
Obiettivi
Poligoni inscritti e
circoscritti.
fondamentali
Saper risolvere e
discutere le equazioni
letterali.
Saper risolvere
Saper operare con i
disequazioni intere,
numeri
• Conoscenze
Saper risolvere sistemi fratte e contenenti
irrazionali e razionali.
• Competenze
numerici e letterali di
modulo. Sistemi di
Saper utilizzare i
• Capacità
primo grado.
disequazioni.
teoremi
Sistemi lineari di tre
equazioni.
Conoscere le principali dell’equivalenza.
trasformazioni
geometriche.
Conoscere e utilizzare i Conoscere e utilizzare i
teoremi relativi alla
teoremi relativi ai
circonferenza e al cerchio.
poligoni inscritti e
circoscritti
Contenuti
fondamentali
Equazioni a due
incognite. Concetto di
funzione .
rappresentazione nel
piano cartesiano della
funzione :y = ax+b;
Disequazioni di primo
Irrazionali.
grado intere,fratte,
Reali.
contenenti modulo.
Equivalenza delle
Sistemi di disequazioni. figure piane.
Sistemi numerici e
letterali di primo grado.
Circonferenza e
cerchio.
Vettori, traslazioni,
rotazioni, isometrie.
Poligoni inscritti e
circoscritti .
punti notevoli dei triangoli.
Verifiche
Almeno una prova
Almeno una prova
Almeno una prova
scritta per valutare le
scritta per valutare le
scritta per valutare le
capacità e le conoscenze
capacità e le conoscenze
capacità e le conoscenze
acquisite.
acquisite.
acquisite.
Pentamestre
Unità di
I
II
III
apprendimento
Periodo di
svolgimento
Febbraio-Marzo
Aprile-Maggio
Maggio-Giugno
Titolo:
Operazioni in R .
Equazioni di secondo
Disequazioni di
Equazioni di grado
secondo grado.
superiore al secondo.
Rapporti e
Sistemi di secondo
• algebra
• geometria
grado. Collegamento
con la parabola.
Teoremi di Euclide e di Proporzionalità.
Pitagora.
Teorema di Talete.
Teoria della misura.
Calcolo delle
probabilità : concetti
fondamentali.
grado.
Obiettivi fondamentali
Conoscere e saper
Conoscere e saper
Conoscere e saper
• Conoscenze
risolvere equazioni di
risolvere le
risolvere le equazioni
• Competenze
secondo grado
disequazioni di
di grado superiore al
• Capacità
intere,fratte e letterali.
secondo grado
secondo e le equazioni
• nozioni di calcolo delle
probabilità
Equazioni irrazionali.
Similitudine.
irrazionali.
Conoscere e utilizzare i intere,fratte,contenenti
teoremi di Euclide e di
Pitagora.
modulo.Sistemi di
Conoscere la teoria
disequazioni.
della misura.
Conoscere e applicare
il criterio generale di
proporzionalità.
Conoscere e saper
risolvere i sistemi di
secondo grado.
Conoscere e saper
applicare la
similitudine
Conoscere il concetto
di evento e di
probabilità.
Conoscere e calcolare
la probabilità di un
evento.
Contenuti fondamentali Equazioni di secondo
Disequazioni di
Equazioni di grado
grado intere,fratte e
secondo grado
superiore al secondo.
letterali.
intere,fratte,contenenti
Sistemi di secondo
Parabola associata
modulo. Sistemi di
all’equazione di 2°: y =
ax2 + bx + c.
disequazioni.
Teoremi di Euclide e di Rapporti.
Pitagora.
Proporzionalità diretta
Teoria della misura.
e inversa; funzioni
associate : y = hx,
grado.
Intersezioni retteconiche.
Similitudine
y = k/x
Teorema di Talete.
Concetti fondamentali
della probabilità.
Eventi e probabilità.
Verifiche
N.B.
Almeno una prova
scritta per valutare le
capacità e le
conoscenze acquisite.
Almeno una prova
scritta per valutare le
capacità e le
conoscenze acquisite.
Almeno una prova
scritta per valutare le
capacità e le
conoscenze acquisite.
L’informatica farà da supporto per la rappresentazione di semplici funzioni matematiche.
La scansione mensile è da ritenersi indicativa.
Nel mese di gennaio si effettueranno interventi di recupero
CONTENUTI DEL TRIENNIO. Matematica A049
MATEMATICA
Terzo anno : Riforma
Geometria analitica (retta - circonferenza - parabola - ellisse - iperbole); equazioni e
disequazioni di vario tipo; discussione del problema geometrico.Esponenziali e Logaritmi con
relative Equazioni e Disequazioni. Interpolazione-regressione e correlazione.
Quarto anno
Goniometria e trigonometria.Problemi
Quinto anno
Analisi (studio di funzioni, integrali) Temi per l’esame di Stato.
SCANSIONE TEMPORALE DI MASSIMA CON CONTENUTI MINIMI PER IL
RECUPERO.
MATEMATICA:
3° anno
Settembre – Ottobre.
Equazioni-disequazioni irrazionali e modulari.
Novembre – Dicembre – Gennaio .
La retta , la circonferenza.parabola
**Febbraio.
Recupero 1° trimestre. Saper operare con la retta e le coniche con l’ ausilio dello strumento
algebrico ..
Marzo.
Ellisse-Esponenziali con relative equazioni e disequazioni
Aprile.
Step di recupero e/o approfondimenti. I logaritmi equazioni e disequazioni
Maggio – Giugno
Iperbole Interpolazione-regressione –correlazione.
**Giugno,obiettivi minimi: L’alunno deve mostrare di saper risolvere i problemi di
geometria analitica.utilizzando adeguatamente lo strumento algebrico in suo possesso.
4°anno Ordinario
Settembre – Ottobre.
Attività di approfondimento e/o recupero della geometria analitica e dell’operatività
algebrica.
Novembre – Dicembre.
Goniometria.
*Febbraio.
Recupero 1° trimestre: L’alunno deve saper risolvere semplici equazioni e disequazioni
goniometriche.
Marzo.
Equazioni e disequazioni goniometriche.
Aprile.
Step di recupero e/o approfondimento.
Maggio – Giugno.
Trigonometria.
*Giugno.
A fine anno l’alunno deve mostrare di saper risolvere semplici problemi trigonometrici con
equazioni e disequazioni.
5° anno.Ordinario
Settembre – Ottobre.
Equazioni e disequazioni esponenziali e logaritmiche.
Novembre.
I limiti con relativi teoremi, gli asintoti.
Dicembre – Gennaio.
Derivate e applicazioni.
Febbraio.
Studio di funzioni.
Recupero primo trimestre: L’alunno deve saper orientarsi con metodi matematici da lui
posseduti a riconoscere e graficare semplici funzioni.
Marzo – Aprile.
Integrali con calcolo di aree e volumi.
Maggio – Giugno.
Simulazione delle prove di esame di stato.
Giugno obiettivo finale: L’alunno deve mostrare di essere in grado di affrontare il compito di
maturità scientifica.
FISICA
3° anno
Riforma
Approfondimenti di meccanica classica (i moti, le forze e l'equilibrio, i principi della dinamica,
le forze e il moto, lavoro ed energia) Legge della Gravitazione. Temperatura e Calore.Modello
microscopico della materia. Cambiamenti di stato .1^ e 2^ Principio della Termodinamica.
Dinamica dei Fluidi
4° anno Ordinario
Quantità di moto, il campo gravitazionale, meccanica dei fluidi, temodinamica, onde (cenni).
5° anno Ordinario
Elettricità - magnetismo -1' induzione elettromagnetica.
3° anno obiettivi minimi:
Febbraio;
L’alunno deve saper applicare le formule in vari contesti e problematiche.
Giugno: L’alunno deve mostrare di possedere un idoneo linguaggio scientifico ,schematizzando
problematiche di vario tipo in modelli matematici con relativa risoluzione (problem-solving).
4° anno obiettivi minimi:
Febbraio:
L’alunno deve mostrare di conoscere gli stati della materia con le relative proprietà
(microscopiche e macroscopiche). Le leggi matematiche che regolano la meccanica dei fluidi.
Giugno: A fine anno l’alunno deve essere in grado di riconoscere le leggi che regolano la
termodinamica con le relative applicazioni.
5° anno:
Febbraio: A fine trimestre l’alunno deve possedere la capacità di individuare un fenomeno
elettrico con le relative leggi e con semplici applicazioni.
Giugno: L’alunno deve avere padronanza sia formale che operativa dei contenuti studiati, deve
mostrare di saper individuare un fenomeno elettrico da uno magnetico, conoscendo le
proprietà e le leggi inerenti.
Il tutto dovrà essere supportato da una fluidità di linguaggio scientifico con capacità di analisi
e sintesi per l’esame di stato.
Classe V A Ginnasio del Liceo Classico nuovo ordinamento
PROGRAMMA DI MATEMATICA
Settembre- Ottobre: Algebra: Richiami sulla fattorizzazione di polinomi e le frazioni algebriche;
Il teorema e Regola di Ruffini; Le equazioni lineari intere, fratte e letterali. Geometria: Richiami
su triangoli; Rette perpendicolari e parallele; Parallelogrammi e trapezi; Circonferenza e cerchio.
Novembre –Dicembre: Algebra: Disequazioni lineari; Funzione; Funzione lineare e retta; Sistemi
lineari. Geometria: Poligoni inscritti e circoscritti; Equivalenza di poligoni; Teorema di Pitagora.
Gennaio: Recupero
Febbraio-Marzo: Algebra: I Radicali. Equazioni di secondo grado; Geometria: Primo e secondo
teorema di Euclide.
Aprile-Maggio: Algebra: Studio del segno del trinomio. Grafico della parabola. Geometria: Le
grandezze e la proporzionalità.
Maggio-Giugno: Algebra: Disequazioni di primo e secondo grado. Geometria: La geometria
analitica.
Classe IA Liceo Classico nuovo ordinamento
PROGRAMMA DI MATEMATICA
Settembre-Ottobre: Divisione fra polinomi e la scomposizione in fattori. Le equazioni di secondo
grado e di grado superiore al secondo. I sistemi di secondo grado. Le disequazioni di secondo
grado. Le disequazioni di grado superiore al secondo. Disequazioni fratte. I sistemi di disequazioni.
Novembre- Dicembre: Equazioni e disequazioni con moduli. Il piano cartesiano. La retta.
Gennaio: Recupero
Febbraio-Marzo: La parabola. La circonferenza.
Aprile-Maggio: Ellisse. Iperbole.
Maggio-Giugno: Le funzioni goniometriche. Le trasformazioni geometriche e grafici di funzioni.
PROGRAMMA DI FISICA
Settembre-Ottobre: Le grandezze. La misura.
Novembre- Dicembre: La velocità. L’accelerazione. I vettori.
Gennaio: Recupero
Febbraio-Marzo: I moti nel piano. Le forze e l’equilibrio. I principi della dinamica.
Aprile-Maggio: Le forze e il movimento. L’energia meccanica.
Maggio-Giugno: La quantità di moto e il momento angolare. La gravitazione.
Classe IIA Liceo Classico vecchio ordinamento
PROGRAMMA DI MATEMATICA
Settembre-Ottobre: Le funzioni goniometriche: la misura degli angoli. Lunghezza di un arco di
circonferenza. Area settore circolare. La circonferenza goniometrica. Le funzioni seno e coseno. La
funzione tangente e cotangente. La funzione secante e cosecante. Le funzioni goniometriche di
angoli particolari. Il periodo delle funzioni goniometriche. Le funzioni goniometriche e le
trasformazioni.
Novembre- Dicembre: Le funzioni goniometriche inverse. Gli angoli associati. Le formule
goniometriche.
Gennaio: Recupero
Febbraio-Marzo: Identità- Equazioni goniometriche.
Aprile-Maggio: Disequazioni goniometriche. Trigonometria: Triangoli rettangoli e applicazioni.
Maggio-Giugno: Trigonometria: Triangoli qualunque e applicazioni.
PROGRAMMA DI FISICA
Settembre-Ottobre: Teoria della misura, Cinematica.
Novembre- Dicembre: Statica. Dinamica.
Gennaio: Recupero
Febbraio-Marzo: Lavoro. Energia.
Aprile-Maggio: Meccanica celeste. Onde.
Maggio-Giugno: Ottica. Acustica.
Classe IIIA Liceo Classico vecchio ordinamento
PROGRAMMA DI MATEMATICA
Settembre-Ottobre: Le funzioni di una variabile reale.
Novembre- Dicembre: Limiti di una funzione di una variabile reale. Funzioni continue.
Gennaio: Recupero
Febbraio-Marzo: Derivata di una funzione: concetti generali. Derivate di funzioni elementari,
teoremi sulle derivate.
Aprile: Studio di funzione.
Maggio-Giugno: Integrali indefiniti e definiti.
PROGRAMMA DI FISICA
Settembre-Ottobre: Termologia
Novembre- Dicembre: Termodinamica.
Gennaio: Recupero
Febbraio-Marzo: Elettricità.
Aprile-Maggio: Recupero
Maggio-Giugno: Magnetismo.
LICEO CLASSICO; FISICA:
2° Liceo classico:
Settembre – Ottobre: Teoria della misura, Cinematica.
Novembre – Dicembre: Statica, Dinamica.
Gennaio: Recupero.
Febbraio – Marzo: Lavoro, Energia, Meccanica celeste.
Aprile: Recupero.
Maggio – Giugno: Onde, Ottica, Acustica.
3° Liceo
Settembre – Ottobre: Termologia.
Novembre – Dicembre: Termodinamica.
Gennaio: Recupero.
Febbraio – Marzo: Elettricità.
Aprile: Recupero.
Maggio – Giugno: Magnetismo.
II Liceo classico
Obiettivi minimi intermedi:
Saper utilizzare sufficientemente un linguaggio specifico appropriato, conoscere in modo
essenziale gli argomenti proposti, risolvere almeno gli esercizi di minore difficoltà,
comprendere il senso dei formalismi matematici introdotti.
Obiettivi minimi finali:
Esprimersi con un linguaggio tecnico specifico, conoscere in modo essenziale gli argomenti
proposti, risolvere gli esercizi di media difficoltà e utilizzare consapevolmente tecniche e
procedure di calcolo comprendendo il senso dei formalismi matematici introdotti.
Corsi di recupero
Conoscere in modo essenziale gli argomenti del programma svolto, esprimersi con linguaggio
quantomeno corretto e sapersi approcciare in modo razionale agli esercizi proposti.
III Liceo classico
Obiettivi minimi intermedi:
Saper utilizzare sufficientemente un linguaggio specifico appropriato, conoscere in modo
essenziale gli argomenti proposti, risolvere almeno gli esercizi di minore difficoltà,
comprendere il senso dei formalismi matematici introdotti.
Obiettivi minimi finali:
Esprimersi con un linguaggio tecnico specifico, conoscere in modo essenziale gli argomenti
proposti, risolvere gli esercizi di media difficoltà e utilizzare consapevolmente tecniche e
procedure di calcolo comprendendo il senso dei formalismi matematici introdotti. Saper
collegare qualche argomento in modo interdisciplinare..
Metodi e strategie
Per il raggiungimento degli obiettivi verranno utilizzate tutte le strategie operative che via
via si renderanno necessarie e indispensabili per una consapevole e appropriata conoscenza
delle varie unità didattiche (lezioni frontali, laboratori,conversazioni didattiche volte a
sollecitare gli interventi degli allievi, esercitazioni guidate o svolte autonomamente, a livello
individuale o in gruppo che tendono a far acquisire sicurezza operativa, attività di ripasso,
recupero, approfondimento). Si precisa inoltre che gli esercizi formulati saranno strutturati
in modo da garantire coerenza logica e non eccessiva difficoltà di calcolo.
INDIVIDUAZIONE DI CRITERI COMUNI RELATIVI ALLE VERIFICHE ED ALLA
VALUTAZIONE
La valutazione avverrà in itinere e si baserà su due tipi di verifiche: verifiche formative e
verifiche sommative.
Si prevedono orientativamente 2 verifiche scritte e/o orali nel trimestre e 3 – 4nel
pentamestre.
Verifiche formative
Correzione esercizi svolti a casa
Verifica individuale delle abilità acquisite
Verifica sommativa
Interrogazione individuale
Verifica scritta tradizionale
Prova scritta strutturata (test a risposta multipla, domande aperte, domande a
completamento parziale.
Si adotteranno i seguenti criteri di valutazione:
I. conoscenza degli argomenti;
2. applicazione corretta degli algoritmi di
calcolo;
3. uso del linguaggio appropriato;
4. coerenza logica;
5. capacità di rielaborazione
personale;
6. ricerca del percorso ottimale.
Attività di Recupero.
Secondo le direttive del Dirigente Scolastico:
A- i docenti del biennio dovranno segnalare quanto prima la necessità di brevi interventi
per prevenire lacune;
B- Recuperi per classi di livello ( 2 settimane a Gennaio, dopo gli scrutini )
1) Saranno segnalati già nella seconda metà di novembre gli alunni con gravi oppure lievi
carenze;
Attività integrative : compatibilmente con le disposizioni del DS, i docenti non
escludono la possibilità di visite guidate, quali: Laboratorio Fisico del Gran Sasso;
osservatori, musei della scienza e della tecnica, nonché tutte le attività proposte dal
comitato tecnico – scientifico.
Stage :Le docenti prof.Tantari e Bezzi in qualità di componenti della commissione
Funzione Strumentale Area2 ,propongono 1)Lo stage per studenti organizzato dal
laboratorio INFN di Frascati 2) Seminari divulgativi tenuti da Docenti della
Università “La Sapienza” di Roma sulla Fisica Quantistica e sulla Fotonica.Per cio’ che
concerne le relative modalità sia di diffusione che di partecipazione, saranno gli stessi
docenti a farsi portavoce.
Progetti : La prof Andreano propone il progetto :”rivoluzione Scientifica” a cui
aderiscono i seguenti colleghi Prof: Fornabaio, Tantari, Pagliei, Vari unitamente ai
colleghi di filosofia prof. Salvatori,Roscioli, Rossi Rosella, Cirillo per le classi terze.
VIAGGI D’ISTRUZIONE :I docenti esaminano le mete proposte dalla Commissione
viaggi e, secondo le indicazione date dal referente prof.Giorietto eliminano 3 mete da
quelle proposte.
Griglie di valutazione :I docenti concordano sulle griglie di valutazione da utilizzare
distinguendole sia in base alla tipologia della disciplina che della classe. Per l’Esame di
Stato ,i docenti adotteranno la griglia fornita dal MIUR nell’a.s. 2011/2012
TEST D’INGRESSO: I docenti esaminano, confrontandoli i risultati ottenuti dagli
alunni delle varie classi. Analizzate le percentuali, si evince il seguente dato: Il
LIVELLO degli alunni in Ingresso è MEDIO-BASSO in Matematica ,mentre in Fisica è
accettabile.Per le classi Terze il livello si aggira intorno alla Mediocrità .
Il Dirigente Scolastico interviene nella riunione Dipartimentale per ricordare e
sottolineare l’importanza di segnalare gli alunni che sin dall’inizio del corrente a.s.
mostrano difficoltà , al fine di ridurre l’abbandono agli studi O il trasferimento ad
altro istituto. Il D.S. sottolinea l’importanza dei test d’ingresso somministrati inizio
anno ,cio’ per rendere maggiormente mirata ed efficace la programmazione comune
con gli obiettivi didattici da perseguire.
Alle 16,55 i docenti intervenuti, esaurita la discussione dei punti all’O.D.G., ritengono
all’unanimità di poter sciogliere la seduta.
Il Referente
Prof. Bianca Andreano